Sommersemester 2013
Funktionentheorie I
Prof. Dr. G. SchumacherZusatzmaterial: Aufgabe 3.3
Wir betrachten die Funktion
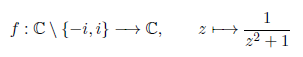
aus Aufgabe 3.3. Da die Funktion von einem zweidimensionalen Raum in einen zweidimensionalen Raum abbildet ist ihr Graph eine Fläche in einem vierdimensionalen Raum und kann aus diesem Grund nicht dargestellt werden. Allerdings kann der Graph des Betrages der Funktion
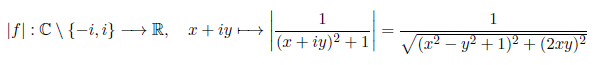
als Fläche in einem dreidimensionalen Raum problemlos dargestellt werden und vermittelt einen zumindest groben Eindruck von der Funktion:
| Darstellung des Betrages der Funktion | Nahaufnahme des interessanten Bereichs |
Wir haben in der Aufgabe für einen beliebigen Punkt
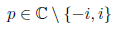
als Potenzreihenentwicklung der Funktion in diesem Punkt das Ergebnis
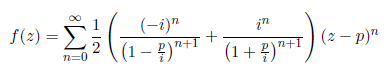
erhalten und gesehen, dass jeweils der Konvergenzradius
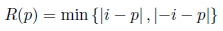
vorliegt. Der Konvergenzkreis ist also stets genau so groß, dass er an die am nächsten zum Entwicklungspunkt gelegene singuläre Stelle der Funktion stößt. Dieses Phänomen ist kein Zufall und wird später im Rahmen der entwickelten Theorie genauer begründet. Die folgende interaktive Zeichnung zeigt den Konvergenzkreis in Abhängigkeit vom Entwicklungspunkt.
|
|
Bemerkung zur Software
Die interaktive Zeichnung wurde mit GeoGebra angefertigt. Die 3D-Modelle wurden mit dem Open-Source Computeralgebrasystem Sage erstellt und werden mit der Open-Source Software Jmol angezeigt.
(Für die Inhalte von externen Seiten übernehme ich keine Verantwortung!)


