Wintersemester 2012/2013
Analysis II
Prof. Dr. G. SchumacherZusatzmaterial: Visualisierung lokaler Extrema
Lokales Minimum
Betrachte die Funktion:
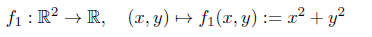
Der Gradient sowie die Hessematrix berechnen sich jeweils zu:
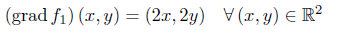
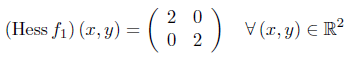
Im Punkt (0,0) liegt ein lokales Minimum vor (sogar ein globales).
Lokales Maximum
Betrachte die Funktion:
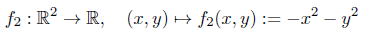
Der Gradient sowie die Hessematrix berechnen sich jeweils zu:
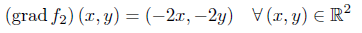
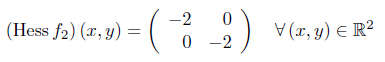
Im Punkt (0,0) liegt ein lokales Maximum vor (sogar ein globales).
Eine Sattelfläche (kein Extremum)
Betrachte die Funktion:
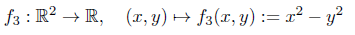
Der Gradient sowie die Hessematrix berechnen sich jeweils zu:
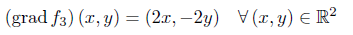
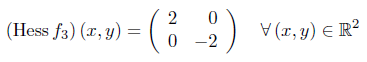
Im Punkt (0,0) verschwindet zwar der Gradient, die Hessematrix ist allerdings indefinit. Also liegt hier kein Extremum vor.
Der Affensattel (kein Extremum)
Betrachte die Funktion:
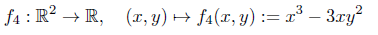
Der Gradient sowie die Hessematrix berechnen sich jeweils zu:
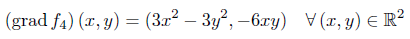
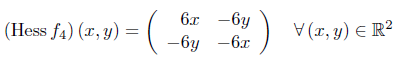
Im Punkt (0,0) liegt kein Extremum vor. Der Satz aus der Vorlesung versagt allerdings, da die Hessematrix in diesem Punkt keine Definitheitseigenschaft aufweist!
Der Name Affensattel rührt übrigens daher, dass er auch für einen Affen eine bequeme Sitzmöglichkeit bietet: Es gibt sowohl zwei Vertiefungen für die Beine als auch eine dritte Vertiefung für den Schwanz des Affen.
Eine Funktion mit vielen verschiedenen lokalen Extrema
Betrachte die Funktion:
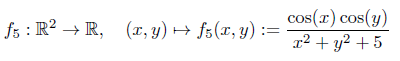
Der Gradient sowie die Hessematrix können zu Übungszwecken selbst ausgerechnet werden!
Bemerkung zur Software
Die 3D-Modelle wurden mit dem Open-Source Computeralgebrasystem Sage angefertigt und werden mit der Open-Source Software Jmol angezeigt.
(Für die Inhalte von externen Seiten übernehme ich keine Verantwortung!)

