Skript Technische Informatik I - Kapitel 2

Übersicht

2.1 Schaltalgebra
2.2 Schaltfunktionen
2.3 Dualitätsprinzip
2.4 BOOLEsche Schaltungen
2.5 Termvereinfachungen
2.6 Grundbegriffe

2.1 Schaltalgebra

Ein Ein-Aus-Schalter

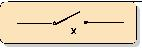
Aus diesen elementaren Schaltern kann man verschiedene Schaltkreise zusammenbauen. Diese Schaltkreise können aus Serienschaltungen

und Parallelschaltungen

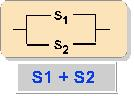
bestehen, wodurch man wiederum Serien-/Parallel-Terme (S/P-Terme) bilden kann.

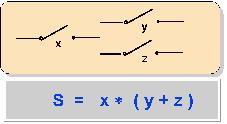
Hier gilt: S = x * ( y + z )

Mit sogenannten Operationstafeln kann man mit den Werten Ein = 1 und Aus = 0 jede Kombination der Komponentenschalter und den Wert darstellen:

+	S2
S1

*	S2
S1

Beispiel eines zusammengesetzten Schaltkreises ( S = x * ( y + z ) ):

x	y	z	x + y	x * (y + z)
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	1	0
1	0	0	0	0
1	0	1	1	1
1	1	0	1	1
1	1	1	1	1

zurück

2.2 Schaltfunktionen

Jeder Schaltkreis realisiert eine Schaltfunktion.

f : {0,1}ⁿ → {0,1}
Bsp.: f : {0,1}³ → {0,1}, f(x,y,z) = x*(y+z)
Abkürzung: 2 := {0,1}

Mehrwertige Schaltfunktionen:

f: 2ⁿ → 2^m
⇒ mehrere Ein- und Ausgänge

Äquivalenz

Jeder Schaltkreis realisiert eine EINDEUTIGE Schaltfunktion.

Zwei Schaltkreise beschreiben dieselbe Schaltfunktion ⇔ die Schaltkreise heißen/sind äquivalent

Beispiel:

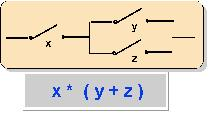
x * (y + z) ⇔ (x * y) + (x * z)

Gleichungen

Zwei Schaltkreise t₁ und t₂ sind äquivalent ⇒ t₁ = t₂

Spezielle Schaltkreise:

der immer geschlossene Schaltkreis heißt: 1
der immer offene Schaltkreis heißt: 0

Wichtige Gleichungen/Umformungsregeln für S/P-Schaltkreise

x + x = x	Idempotenz	x * x = x
x + y = y + x	Kommutativität	x * y = y * x
x + (y + z) = (x + y) + z	Assoziativität	x * (y * z) = (x * y) * z
x * (x + y) = x	Absorption	x + (x * y) = x
x * (y + z) = x * y + x * z	Distributivität	x + (y * z) = (x + y) * (x + z)
x + 0 = x		x * 1 = x
x + 1 = 1		x * 0 = 0 /td>

Mit obigen Gleichungen bildet eine nichtleere Menge M mit den Verknüpfungen + und * und den Elementen 0 und 1 einen distributiven Verband (M; *, +, 0, 1)

zurück

2.3 Dualitätsprinzip

Um einen dualen Term t^d zu einem Term t zu erhalten, ersetzt man ...

... jede 0 durch eine 1 und umgekehrt

... jedes + durch * und umgekehrt

Definitionen:

0^d = 1, 1^d = 0;
x^d = x;
(u * v)^d = u^d + v^d, (u + v)^d = u^d * v^d
⇒ t = t^d^d, (t₁ = t₂ ⇒ t₁^d = t₂^d).

Negation

S’ ist Negation (oder Komplement) von S (beides Schaltkreise)
⇒ (S’ geschlossen ⇔ S offen) und umgekehrt
Zweifache Negation: S’’ = S

zurück

2.4 BOOLEsche Schaltungen

Schaltkreis, in dem S/P-Schaltung und Negation verwendet werden darf
Entsprechender Term heißt: BOOLEscher Term (analog S/P-Terme)

BOOLEsche Gleichungen (zusätzlich zu den Gleichungen des distributiven Verbandes):

(x + y)’ = x’ * y’	DE MORGAN'sche Regeln	(x * y)’ = x’ + y’
x + x’ = 1	Komplementregeln	x * x’ = 0
x’’ = x

Distributive Verbände mit 0 und 1 und obigem Komplement heißen BOOLEsche Algebren.

zurück

2.5 Termvereinfachungen

Mit den zuvor vorgestellten Gesetzmäßigkeiten lassen sich Schaltfunktionen wesentlich vereinfachen.

So wird aus dem Term: x´y´z´ + x´y´z + x y´z´+ x y z

durch Anwendung von Distributivität (x´y´z´ + y´y´z = x´y´(z´+z)),

Kommutativität (z + z´= z´+ z),

Komplement (z´+ z = 1),

der Regel x * 1 = x,

Absorption (x y´z´= x y´z´+ x´y´z´),

Distributivität (x y´z´+ x´y´z´= (x + x´) y´z´) und erneut Komplement und der Regel x * 1 = x

daraus der Term: x´y´ + y´z´+ x y z, welcher doch um einiges einfacher ist.

zurück

2.6 Grundbegriffe

Wenn die Stelligkeit von Schaltfunktionen n >= 1 ist, kann man folgende Begriffe definieren:

Literal: Ein Literal ist eine Variable x_i (positives L.) oder deren Negation x_i´ (negatives L.) und wird mit
x_i¹ ( = x_i) oder x_i⁰ ( = x_i´) bezeichnet.
Monom: Ein Monom ist eine Konjunktion von Literalen bezeichnet mit x_i₁^e₁… x_{i_k}^e_k für k ≤ n
Klausel: Eine Klausel ist eine Disjunktion von Literalen bezeichnet mit x_i₁^e₁+…+ x_{i_k}^e_k für k ≤ n

Monome bzw. Klauseln der Länge n = k heißen Min- bzw. Maxterme.

Zu einer gegebenen Schalttafel kann man nun mit Hilfe von Min- bzw. Maxtermen Schaltfunktionen in so genannter Disjunktiver bzw. Konjunktiver Normalform konstruieren.

Bei der Konstruktion einer Disjunktiven Normalform (DNF) nimmt man die Eingaben bei denen f(x₁,…, x_n) = 1 ist und konstruiert zu jeder Eingabe einen Minterm. Das heißt für die Schalttafel werden die Fälle betrachtet in der in der rechten Spalte eine 1 steht. Aus diesen Zeilen konstruiert man die entsprechenden Minterme in dem man, wenn f(x) = 0 x´ und wenn f(x) = 1 x notiert und diese multipliziert. Diese Minterme für die einzelnen Zeilen werden anschließend addiert.

i	x	y	z	g(x,y,z)
0	0	0	0	1	⇒ Minterm: (x'y'z')
1	0	0	1	1	⇒ Minterm: (x’y’z)
2	0	1	0	0
3	0	1	1	0
4	1	0	0	1	⇒ Minterm: (xy’z’)
5	1	0	1	0
6	1	1	0	0
7	1	1	1	1	⇒ Minterm: (xyz)

⇒ DNF : g(x,y,z) = (x’ y’ z’) + (x’ y’ z) + (x y’ z’) + (x y z).

Analog kann man mit Hilfe der Maxterme eine Darstellung einer Schaltfunktion zu einer gegebenen Schalttafel konstruieren, in der so genannten Konjunktiven Normalform (KNF), allerdings muss man die Zeilen betrachten, in denen in der rechten Spalte 0 steht. Aus diesen Zeilen konstruiert man die entsprechenden Maxterme in dem man, wenn f(x) = 0 x und wenn f(x) = 1 x´ notiert und diese addiert. Diese Maxterme für die einzelnen Zeilen werden anschließend multipliziert.

i	x	y	z	g(x,y,z)
0	0	0	0	1
1	0	0	1	1
2	0	1	0	0	⇒ Maxterm: (x+y’+z)
3	0	1	1	0	⇒ Maxterm: (x+y’+z’)
4	1	0	0	1
5	1	0	1	0	⇒ Maxterm: (x’+y+z’)
6	1	1	0	0	⇒ Maxterm: (x’+y’+z)
7	1	1	1	1

⇒ KNF: g(x, y, z) = (x + y’ + z) + (x + y’ + z’) + (x’ + y + z´) + (x’ + y’ + z)

NAND und NOR

Die Schalttafel der NAND – / NOR – Funktion entsteht durch negieren der Schalttafel der And – / Or – Funktion, d.h. an die Stelle jeder 1 tritt eine Null und umgekehrt. Sowohl die Menge {NAND} als auch die menge {NOR} ist funktional vollständig, was bedeutet, dass man allein mit der NAND –Funktion (der NOR – Funktion) sämtliche anderen Funktionen darstellen kann.
Zum Beispiel: x + y = (x NAND x) NAND (y NAND y)
oder: x´= (x NAND x).

zurück

Zur Hauptseite

Zum nächsten Kapitel