Script Computer Engeneering - Part VI

6.Representation of data in the Computer, Computer Arithmetic


6.1 Negative Numbers, Complement on Two


In the representation of the complement of two the positive numbers are traversed first, then the negative numbers in reversed order.


0000     =    0       1000     =     - 8
0001     =    1       1001     =     - 7
0010     =    2       1010     =     - 6
0011     =    3       1011     =     - 5
0100     =    4       1100     =     - 4
0101     =    5       1101     =     - 3
0110     =    6       1110     =     - 2
0111     =    7       1111     =     - 1

On the complement of two, the first number stands for the algebraic sign.


Value of a positive number

W = ∑ i=0,n-1 (bi* 2(n-1-i))

Example

an integer-number shall be displayed as an 8 bit number to the base of 2
W(000011012 ) =
    0*27 +..+ 0*24 + 1*23 + 1*22 + 0*21 + 1*20 = 8 + 4 + 1 = 1310
 
Value of a negatve Number

W = - (2n - ∑i=0,n-1 (bi* 2(n-1-i)))

Building the difference of two integers


    decimal        dual   
    17              00010001   
    +(-14)        11110010   
    = 3             00000011  


Complement on two on the number-circle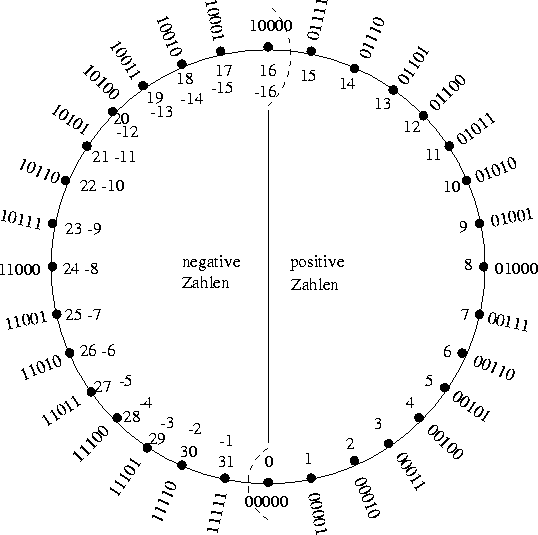


image 1


Complement on two (Definition)

The bit-sequence
zn    zn-1    zn-2    . . .    z1   z0

represents the binary number
- zn *  2n   +  zn-1 * 2(n-1) + zn-2 * 2(n-2)  + . . .  +  z1 * 21  + z0


Complement on two for n=3

For n = 3 follows:

1000 = - 8    1100 = - 4    0000 = 0    0100 = 4
1001 = - 7    1101 = - 3    0001 = 1    0101 = 5
1010 = - 6    1110 = - 2    0010 = 2    0110 = 6
1011 = - 5    1111 = - 1    0011 = 3    0111 = 7


Negation on the Complement on Two

I you add a number to itscomplement, the result is 111 ... 1111

111 .... 1111       =  - 2n +  2(n-1) +  ...  + 21 + 1

                          =  - 2n +  ( 2n - 1)   =  - 1

A number plus its complement results into the representation of -1

So, negating a number is done by adding 1 to its complement.


Basic Arithmetic Operations for the Complement on Two

Addition: Use of the same hardware as on the signless numbers
              S=A+B; Ci=Carry-In = 0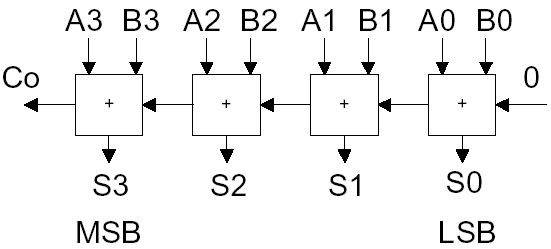

image 2
 
-5 + 6 = 1

in representation on the complement on two :

1011 + 0110 = 0001  (watch out when going out of the range)

Negation

5 in complement on two : 0101

-5 in complement on two : 1011
 complement all bits, then add 1

Subtraction: Addition with bit-inversion of the subtrahend and   
Carry-In on the LSB     D=A-B, Ci=Carry-In=1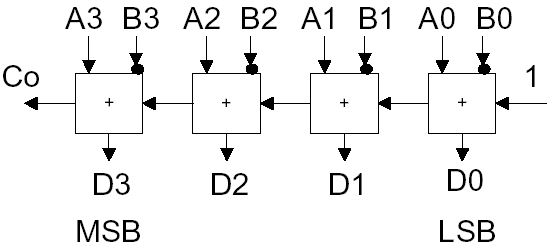

image 3

negate the second operand, then add


Complement on two-Addition/Subtraction und Overflow

Overflow = The representable number-range is exceeded

Overflow when adding numbers in complement on two:

Examples:

-3 + (-6) = -9
1101 + 1010 = 1 0111 = +7
5 + 6 = 11
0101 + 0110 = 1011  = -5

A sure symptom for an overflow:

Summands of the same sign  ≠ Sign of the sum
=> Carry-In in sign-position  ≠ Carry-Out of sign-position


Overflow at subtraction on numbers in complement on two:

Example:

-3 - (+6) = -9
=>1101 - 0110 => 1101 + 1001 + 0001 = 1 0111 = +7

A sure symptom for an overflow:

Minuend & complem.subtrahend same sign ≠ sign of the difference
=> Carry-In in sign-position  ≠ Carry-Out of sign-position

<back>


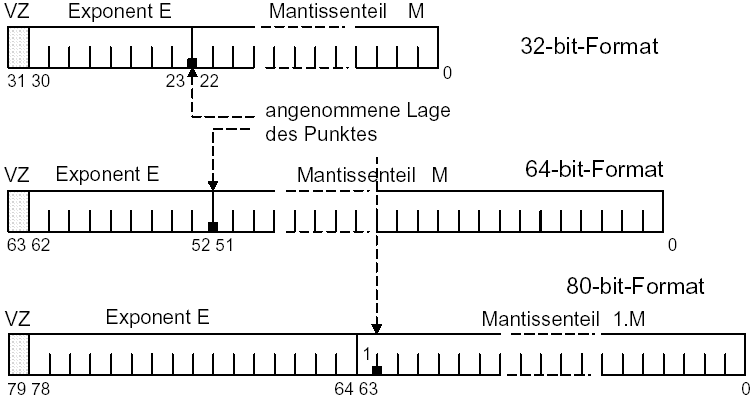
6.2 Floating-Point Numbers



Rational Numbers as Binary Integers

In a general number-system with a base-number b, also rational numbers can be defined:

With the numbers Xn, Xn-1, ..., X1, X0 and Y1, Y2, ..., Ym-1  with Xi , Yj C {0, 1, ..., b-1}
the broken number

                 X = (Xn Xn-1 ... X1 X0 . Y1 Y2 ... Ym-1 )b   

with the number-value

X = Xn*b^n  +...+ X1*b^1 + X0 + Y1*b^(-1) + Y2*b^(-2)  + ... + Ym*b^(-m)
  
can be built.

Example:

broken binary-numbers
0 . 1,  0 .01,  0 .11,  1 .11,  111 .111, 11011101011 .100111011

broken decimal-numbers
0 . 5,  0 . 25,  0 . 75,  1 . 75,  7 . 875,  1771 . 6162109375


Floating-Point Numbers

Analog to 4711 = 0.4711 * 104
binary floating-point numbers are built.

Floating point numbers consist of:

- the sign V
- the exponent E
- the mantissa M

V, E and M represent the number (-1)V * M * 2E


Sign, Exponent and Mantissa

The Mantissa consists of binary-numbers m1 ... mn and is interpreted as

m1 x 2(-1) + m2 x 2(-2) + ... + mn x 2(-n) 

The sign-bit shows if the number is positive or negative.

The Exponent is a binary-number, for example in the range of -128 to +127.


Scaled Floating-Point Numbers

By shifting the kommata and adaptation of the exponent it can be reached that the first position of the mantissa is 1.
 
This representation is named normed floating-point representation.

0.01010111 * 214 = 0.1010111 * 213 = 1.010111 * 212 (normed)


Norm for Floating-Point Numbers:

Exponent integer, 1 ≤ amount of the mantissa < 2

No complement on two, but amount/sign-representation for the mantissa

single precision: 23 bit mantissa, 8 bit exp, 1 bit sign

double precision: 52 bit mantissa, 11 bit exp., 1 bit sign

1 ≤  Amount of the mantissa < 2  => binary between 1,000... and 1,111..
                                           => 1 befor the kommata not necessary (hidden one)

image 5



Transformation of Floating-Point Numbers into the binary IEEE-754 Format

Given: ± M 2E, 1 ≤ M < 2 , -126 ≤ M ≤ 127

IEEE -754: V=sign-bit(0 = positive, 1 = negative)
                Mantissa = sign-less representation of (M-1) = 0, m1...m23
                Exponent = sign-less representation of (E+127) = e7 e6... e0
                => saved will be a 32 bit data-word


                image 6

Example:

Transformation of 1234567,8910 to the IEEE -754 format

1234567,89 = 220,23557474 = 20,23557474 * 220 = 1,177375686 * 220
                  = 1,001011010110100001111110001100102 * 220
                  => V = 0
                  Exponent = 20 + 127 = 100100112
                  Mantissa =  ,00101101011010000111111

  
<back>

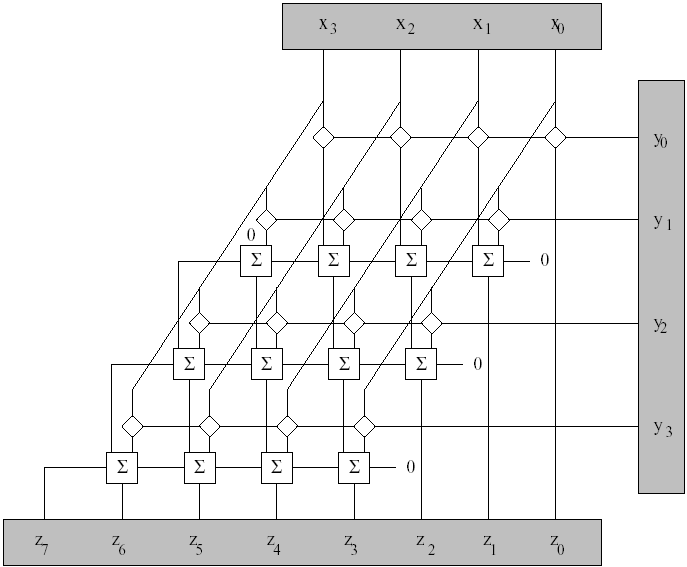
6.3 Multiplication

Multiplication of binary-numbers

The multiplication of binary-numbers can be reduced to addition and shift-operations.

The binary-representation of X is shifted each time for one digit to the left. If the corresponding position of Y equaled 0, it's annullated, elseway added.

To realize the multiplication with a computer, there exists the so called Barrel-Shifter. It consists mainly of AND-cirquits and 1-bit adding-cirquits. The bitwise multiplication is the same as the logical and-operation.

If X and Y are the input-registers with the bit-digits X(n-1),....,X(0) bzw. Y(n-1),....,Y(0) , a gate is to be built where every crossing-point X(i) with Y(i) is linked through an AND-cirquit. By the adding-cirquits the columns are added. The carry-bit is carried through row by row. An overflow in a row will be added to the next column.

For the result of a multiplication the register should be double as broad as the input-register.

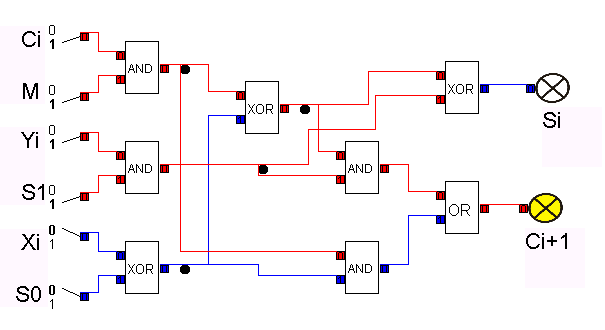
The 1-bit ALU

To construct a multiple-bit-ALU, it is enough to put several 1-bit-ALUs in a row.

For the arithmetical operations, a carry from one to the next bit-position has to be considered. So that for each 1-bit-ALU an extra carry-in and carry-out has to be built.

To implement 8 several operations, a 1-bit-ALU with 6 inputs has to be realized: 3 inputs M, S0 and S1, a carry-input Ci, and also the inputs for Xi and Yi. But only two outputs are needed. Si for the result of the operation and C(i+1) for the new carry. The logical cirquit-plan is shown here:

 

<back>

 

main