Bisher wurden Schaltkreise aus booleschen Termen entwickelt, die wiederum aus einer Schaltfunktion entstanden. Somit konnten diese Schaltkreise elementare Operationen wie Addition oder Multiplikation realisieren. Eine Speicherzelle konnte bisher noch nicht entwickelt werden. Dazu benötigt man rückgekoppelte Schaltungen. Dabei bedeutet rückgekoppelt, dass der Ausgang eines Schaltgliedes wieder in dessen Eingang geleitet wird.
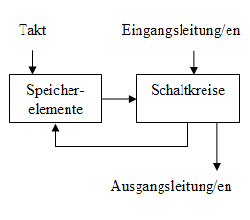
Ein Schaltwerk besteht also zusätzlich aus:

Schaltwerke befinden sich zu gegebener Zeit in einem Zustand Q. Ein solcher Zustand ist beispielsweise durch die Werte der Ausgangsleitung/en zu diesem Zeitpunkt charakterisiert.
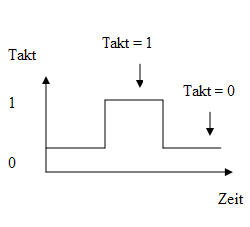
Eine Zustandsänderung erfolgt nur zu bestimmten diskreten Zeitpunkten:
Dabei bedeutet "Eintreffen eines Taktes", dass eine 1 auf der Taktleitung anliegt.
Binäre Speicherelemente sind kleinste logische Bausteine zur Aufbewahrung von Informationen. Gespeichert wird einer der Zustände 0 oder 1. Die Realisierung erfolgt durch Schaltwerke.
Ein Zustand Q(n) wird durch den gespeicherten Wert und durch die Werte auf den Eingangsleitungen im n-ten Taktzyklus bestimmt.
Der gespeicherte Wert steht über eine Ausgangsleitung zur Verfügung. Eine zusätzliche Ausgangsleitung liefert den negativen gespeicherten Wert, also Q(n)'.
Gedanke: Durch zwei besondere Eingänge kann der Zustand Q im nächsten Takt geändert werden.
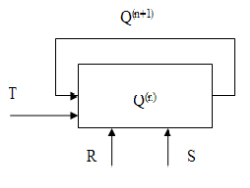
Es gilt:
Damit ergibt sich folgende Schalttabelle für den RS-Flip-Flop (beachte T=1):
| S | R | Q(n) | Q(n+1) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | n.d. |
| 1 | 1 | 1 | n.d. |
Daraus folgt die (vereinfachte) Schaltfunktion für Q(n+1):
...und damit die Schaltung für Q(n+1):
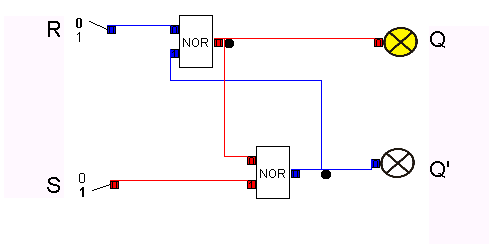
Damit wird folgendes Schaltsymbol für den RS-NOR-Flip-Flop eingeführt:
Mit Einbeziehung des Taktes T ergibt sich folgende Schaltfunktion für Q(n+1):
...und damit die Schaltung für Q(n+1):
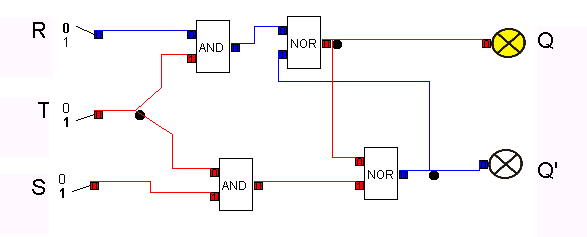
Damit wird folgendes Schaltsymbol für den getakteten RS-NOR-Flip-Flop eingeführt:
Ersetzt man alle NOR-Glieder eines RS-NOR-Flip-Flops durch NAND-Glieder, so erhält man den RS-NAND-Flip-Flop. Dessen Verhalten ist dual zu dem des RS-NOR-Flip-Flops.
Aus

wird
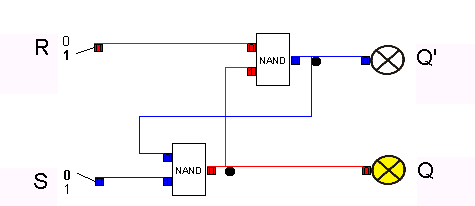
Der RS-NAND-Flip-Flop ist nur aktiv, wenn R=0 bzw. S=0 gilt.
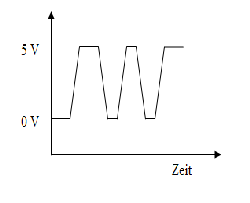
Eine elementare Verwendung eines Flip-Flops ergibt sich für das Entprellen eines (mechanischen) Schalters, z.B. einer Taste der Tastatur. Beim Drücken einer Taste beobachtet man, dass der Schalter prellt. Dies bedeutet, dass die Spannung zwischen dem Ausgangswert 0 Volt und dem gewünschten neuen Wert (z.B. 5 Volt) für eine kurze Weile hin- und herspringt. Dadurch würde es zu dem nicht gewünschten Effekt kommen, dass mehrere Zeichen dieser Taste auf dem Bildschirm erscheinen.
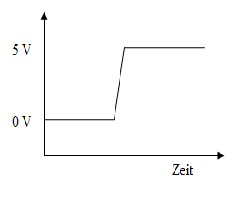
Idealerweise sollte das Zeit-Spannungs-Diagramm eines gedrückten Schalters jedoch folgendes Aussehen haben:
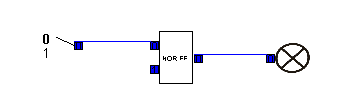
Um einen solchen Schalter zu entprellen, bedient man sich eines Flip-Flops:
Der prinzipielle Aufbau einer Speicherzelle mithilfe eines Flip-Flops ergibt sich bereits aus dem Aufbau und der Wirkungsweise desselben. Da ein Speicher jedoch aus einer Vielzahl solcher Speicherzellen besteht, muss sichergestellt sein, dass eine solche explizit ausgewählt werden kann, um ihren Inhalt entweder zu lesen oder zu verändern. Dazu werden zusätzliche Schaltglieder eingefügt:
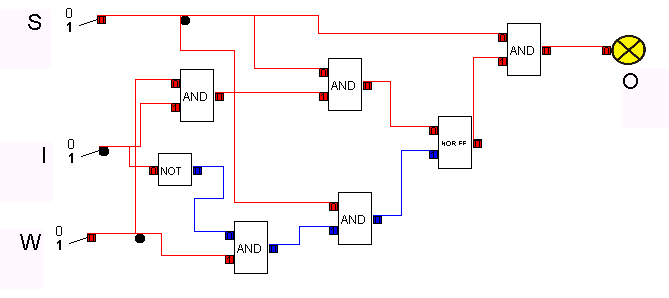
Bedeutung der Eingänge und Wirkungsweise:
Vereinfachtes Schaltbild einer Speicherzelle:
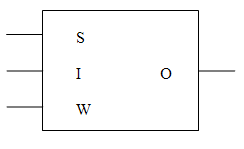
Ein Register ist eine Gruppe von Speicherzellen. Die Anzahl der Speicherzellen in einem Register ist meist der Wortgröße, also 8 Bit, 16 Bit oder 32 Bit. Da man nie einzelne Zellen eines Registers anspricht, kann man die Select- und Write-Eingänge der einzelnen Zellen miteinander verbinden.
Blockschaltbild für einen 4-Bit-Register:
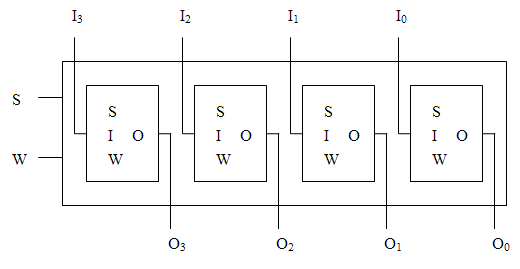
Der Transfer eines n-Bit-Registers X in ein n-Bit-Register Y realisiert man, indem man die Ausgänge von X mit den entsprechenden Eingängen von Y verbindet. Dazwischen wird jeweils ein Schalter gesetzt, der durch ein AND-Gatter realisiert wird. Die Schalter werden durch ein gemeinsames 1-Signal (Bus) geöffnet, so dass die Information vom X-Register zum Y-Register fließen kann. Beide Select-Eingänge sowie der Write-Eingang des Y-Registers müssen ebenfalls aktiviert sein.
Blockschaltbild für den Transfer zwischen zwei 4-Bit-Registern:
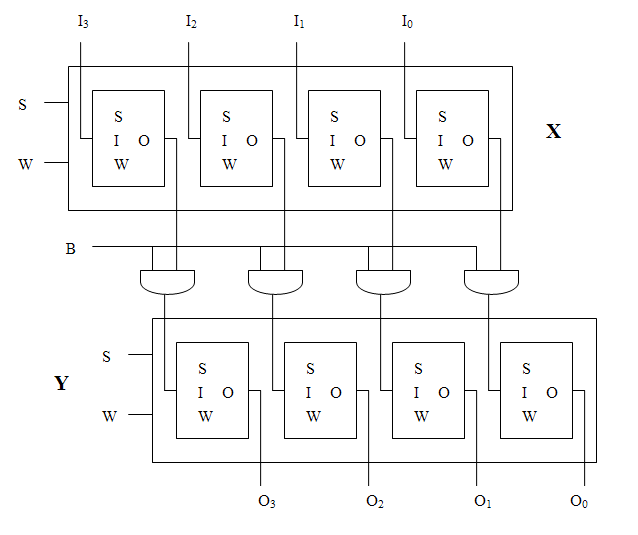
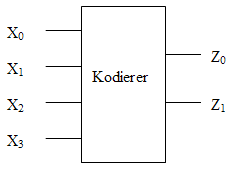
Ein Kodierer hat 2n Eingänge und n Ausgänge. Wenn am k-ten Eingang der Wert 1 anliegt und an allen anderen Eingängen der Wert 0, dann wird die Zahl k an den Ausgängen binär dargestellt. Für alle anderen Inputs ist das Ergebnis unspezifiziert.
Schalttabelle für einen Kodierer mit 22 Eingängen X0 - X3 und 2 Ausgängen Z0, Z1:
| X0 | X1 | X2 | X3 | Z0 | Z1 |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 |
Vereinfachtes Schaltbild eines Kodierers mit 22 Eingängen X0 - X3 und 2 Ausgängen Z0, Z1:
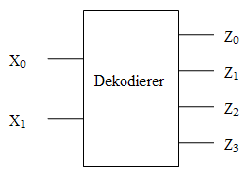
Ein Dekodierer erhält man, wenn man Ein- und Ausgänge vertauscht. Die Folge von 0-en und 1-en am Eingang wird als Binärzahl k interpretiert und der Ausgang Zk auf 1 gesetzt. Alle anderen Ausgänge auf 0. In der praktischen Anwendung wird am Eingang eines Dekodierers die binäre Adresse einer Speicherzelle anliegen. Am Ausgang wird dann genau die Leitung, die zu der gewünschte Speicherzelle führt, aktiviert.
Schalttabelle für einen Dekodierer mit 2 Eingängen X0, X1 und 22 Ausgängen Z0 - Z3:
| X1 | X0 | Z0 | Z1 | Z2 | Z3 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
Vereinfachtes Schaltbild eines Dekodierers mit 2 Eingängen X0, X1 und 22 Ausgängen Z0 - Z3:
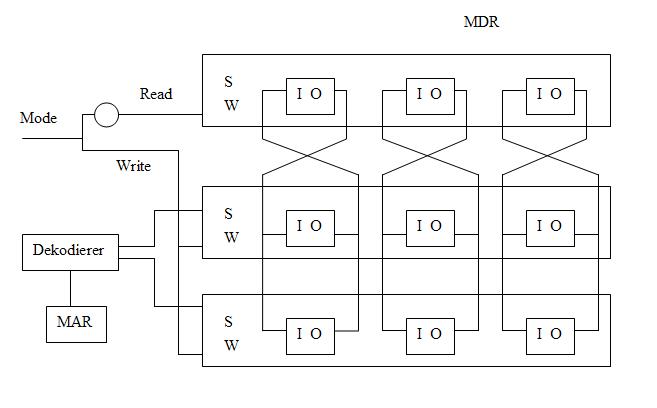
Ein adressierbarer Speicher wird mit folgenden Komponenten verwirklicht:
Beispiel eines adressierbaren Speichers mit Wortlänge 3 und einer Speichermöglichkeit von 2 Worten: