• Main
• Research
• Publications
• Teaching
• CV
• Group

Underlying principles

One of the traditional goals in numerical harmonic and functional analysis, is the development of efficient methods to assemble (synthesize) or decompose (analyse) functions or operators into well-understood basic building blocks. Analysis relies on the understanding of appropriately chosen basic components and on determining the weight of each component in a given signal. For example, a picture can be decomposed into patches of red, green, and blue of varying intensities. The dual operation is signal synthesis. Using the same building blocks as in the analysis step, we can assemble or reassemble signals and transformations of our liking. Returning to our example, we could, starting from scratch, draw a picture by choosing patches of red, green, and blue and intensities freely.

In digital communications, synthesis and analysis are applied in succession. To transmit digital data through a medium, an analog signal is formed using a synthesis step. Here, the digital information is embedded in the weights. The receiver then performs an analysis of the obtained signal to extract the weights and with it the digital data. The principal objective is to design building blocks that are robust against disturbances present in transmission channels.

Within the past decade, mathematical contributions to these objectives had an tremendous impact on signal processing and communications engineering: wavelet bases were designed to analyze images (jpeg2000), and Gabor systems are currently used to transmit data through wired or wireless channels (OFDM). A wavelet basis consists of functions, which are all equal in shape but which are translated (shifted in time or space) or stretched copies of each other. The building blocks in Gabor theory on the other hand are functions, which are modulated (frequency-shifted) and translated (shifted in time or space) copies of each other.

In recent years, our research within the framework described above focused on time--frequency analysis of operators and Gabor analysis, and their applications in communications engineering. (For educational material, visit the website of our Summer Academy Progress in Mathematics for Communication Systems.)

Some Research Directions

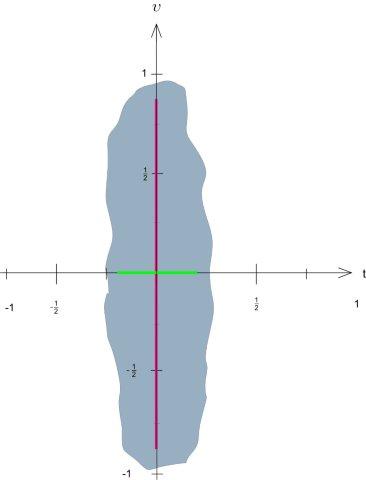
		A sampling theory for operators and channel measurements The so-called classical sampling theorem states that a bandlimited function can be recovered from its samples as long as a sufficiently dense sampling grid is used. In the recently developed sampling theory for operators, bandlimited functions are replaced by pseudodifferential operators that have band-limited Kohn--Nirenberg symbols. We showed, for example, that if the bandlimitation is described by a bounded Jordan domain of measure less than one, then the operator can be recovered through its action on a distribution defined on an appropriately chosen sampling grid. Further, an operator band-limited to a Jordan domain of measure larger than one cannot be recovered through its action on any tempered distribution whatsoever, pointing towards a fundamental difference to the classical sampling theorem where a large bandwidth can always be compensated through a sufficiently fine sampling grid. The dichotomy depending on the size of the bandlimitation in phase space is a manifestation of Heisenberg's uncertainty principle. Figure. Our operator sampling results apply to all pseudodifferential operators whose Kohn- Nirenberg symbol is bandlimited to a Jordan domain of area less than one (e.g., the grey region). These results extend Shannon's sampling theorem which is equivalent to the identifiability of operators whose Kohn-Nirenberg symbol is bandlimited to a segment of the frequency shift axis (red) and the fact that time-invariant operators can be identified from their action on the impulse. The latter holds since the Kohn-Nirenberg symbols of time–invariant operators are bandlimited to the time shift axis (green). Collaborators: John Benedetto, Yoon Mi Hong, Werner Kozek, David Walnut, Peter Rashkov Publications: 13,14,15,16,19,23,25,28,31,32,34
		Sparse time--frequency representations Efficient algorithms aiming at the recovery of signals and operators from a restricted number of measurements must be based on some a-priori , information about the object under investigation. In a large body of recent work, the signal or operator at hand is assumed to have a sparse representation in a given dictionary. A typical example in this realm is the recovery of vectors that are sparse in the Euclidean basis, that is, of vectors which have a limited number of nonzero components at unknown locations. Such a vector is to be determined efficiently by a small number of linear measurements which are given by inner products with appropriately chosen analysis vectors. The difficulty in this body of work lies in the fact that sparsity conditions as those mentioned above are met by collections of linear subspaces of signal or operator spaces, collections whose unions are nonlinear. To circumvent a combinatorial and therefore unfeasible exhaustive search, efficient alternatives such as $\ell_1$-minimization (Basis Pursuit) have been proposed in the sparse representations and compressed sensing literature. In this work, we consider sparse representations in terms of time--frequency shift dictionaries, and investigate recovery conditions similar to the ones for Gaussian, Bernoulli and Fourier measurements. Figure: Empirical verifcation of Basis Pursuit recovery using a Gabor system with random window in the noisy setting (25 dB signal to noise ratio). Contours of the fitted logistic regression model (gray), the 93% success rate contour (dash), and 1/(2 log n) (solid). See publication 13. Collaborators: Holger Rauhut, Jared Tanner Publications: 21,25,30
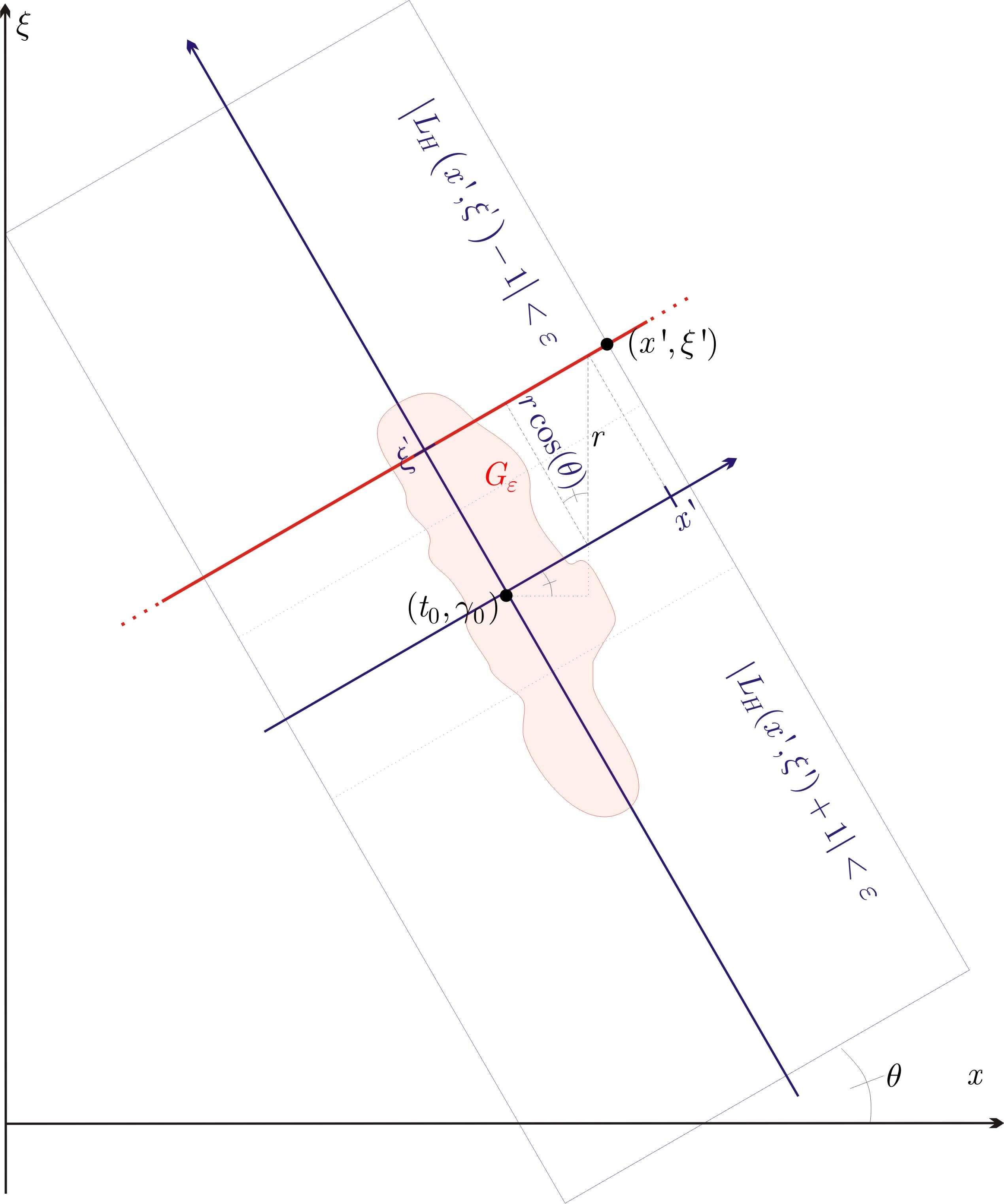
		Pulse design and time-variant communication channel models Our goal is the mathematical analysis and optimisation of orthogonal frequency division multiplexing (OFDM) schemes in view of transmission stability in time-invariant, but also wireless and other time variant environments. In fact, one of the cornerstones of our work is the analysis of the perturbation stability of different bases when used in wireless communication channels. For example, we derived estimates which relate the worst case distortion of a function to the functions time-frequency concentration and the time variant channel operators spreading support. Further, we continue our work on the modelling of narrowband finite lifelength systems such as wireless radio communications by smooth and compactly supported spreading functions. Our results include the exact implementation of certain classes of so-called underspread operators and the derivation of a fast algorithm for computing the matrix representation of a channel operator with respect to pulseshaped OFDM bases. Another line of research within this realm considers the analysis and reduction of the crest factor (equivalently, the peak to average ratio of OFDM signals. Figure: Construction of a channel spreading function whose operator causes a large distortion to a function with time-frequency support G. Collaborators: Niklas Grip, Kurt Jetter, Werner Kozek, Georg Zimmermann Publications: 4,6,7,9,10,18,22,28
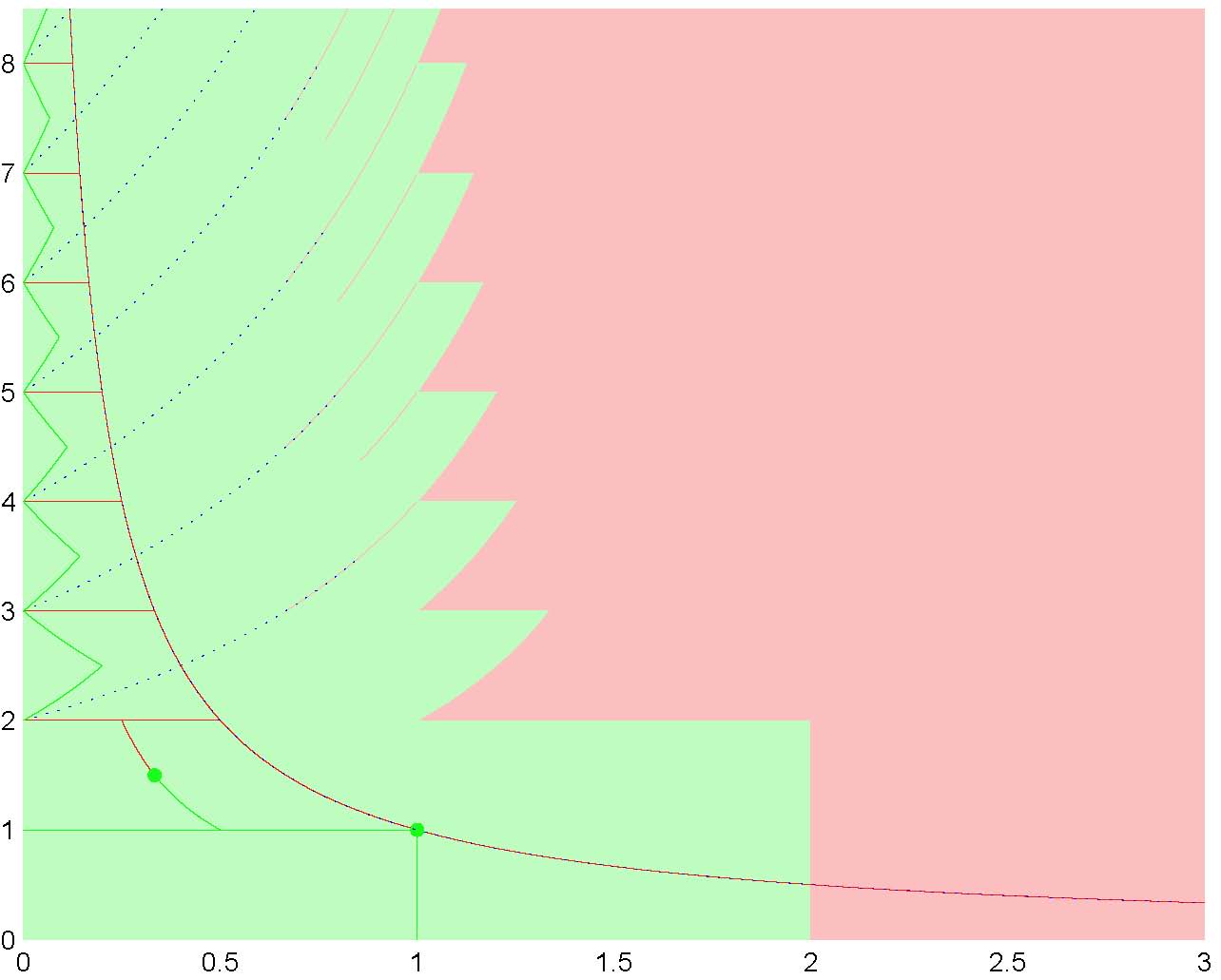
		Gabor frames on the real line Within Gabor frame theory proper, we have addressed a number of structural questions. In one of our recent results, we point out that Gabor systems generated by a continuous and compactly supported prototype function, and frequency-shift parameters 2, 3, . . . do not form frames. This result was a surprise for us, as it had been generally assumed that any "nice" window g and "reasonable" choice of time- and frequency-shift parameters yield Gabor frames. Our observation demonstrates that even for window functions that are perfectly natural in approximation theory and wavelet theory, the Gabor frame parameters have to be chosen extremely carefully. In our work on Gabor multipliers we proved, in the case of identical analysis and synthesis windows, we proved, that the generating operators for such multipliers are either Riesz bases (exact frames) or not frames for their closed linear spans. The same dichotomy conclusion is valid for general rank one operators under mild and natural conditions. An additional research interest is the construction of Gabor frames of functions for arbitrary time-frequency lattices or irregular discrete sets in the time-frequency plane. Orthonormal bases have been constructed for arbitrary time-frequency lattices but they consist of characteristic functions which are poorly localized in frequency. Hence, the fundamental problem of constructing Gabor frames or Riesz bases of well behaved functions for arbitrary lattices remains open. Figure: Illustration of lattice parameters (1/a,1/b) so that the rank one operators that compose a Gabor multiplier with respect to the characteristic function on the unit interval fails (in red) to be Riesz basis in the space of Hilbert-Schmidt operators. Collaborators: John Benedetto, Karlheinz Groenenig, A.J.E.M. Janssen, Norbert Kaiblinger Publications: 11,14,28
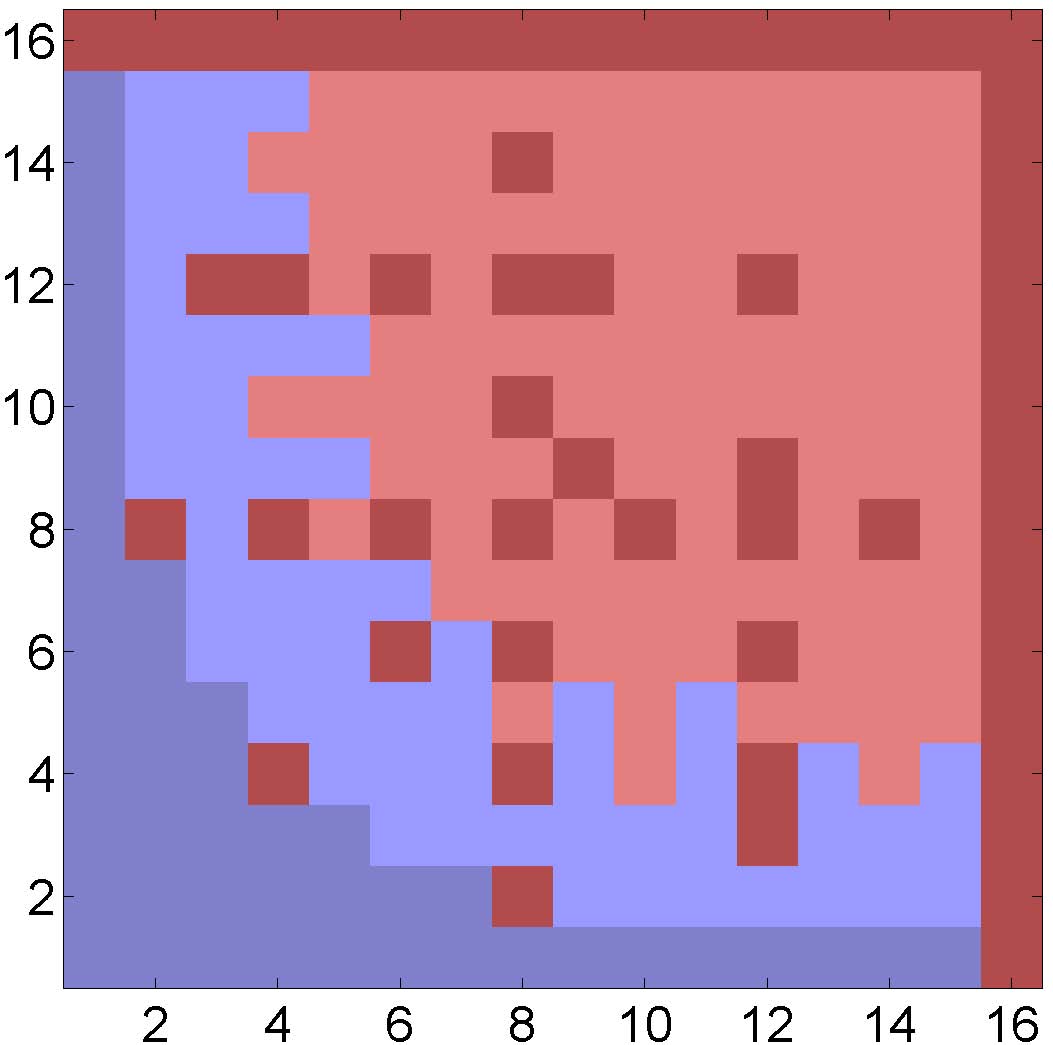
		Uncertainty principles and time-frequency analysis on finite Abelian groups Uncertainty principles establish restrictions on how well localized the Fourier transform of a well localized function can be and vice versa. In the case of a function defined on a finite Abelian group, localization is generally expressed through the cardinality of the support of the function. A classical result on uncertainty states that the product of the number of nonzero entries in a vector representing a nontrivial function on an Abelian group and the number of nonzero entries in its Fourier transform is not smaller than the order of the group. This result has been improved for any nontrivial Abelian group by Meshulam. In oru work, we established corresponding results for joint time-frequency representations, that is, to obtain restrictions on the minimal cardinality of the support of joint time-frequency representations of functions defined on finite Abelian groups. Applications of our results range from sparse matrix identification to the construction of a generic class of Gabor frames which are maximally robust to erasures. Figure: Illustration of the uncertainty principle for vectors of finite Abelian groups. We display in red those support size pairs achievable by a vector on the group (Z_2)^4 and its Fourier transform. Results are based on numerical experiments. Collaborators: Jim Lawrence, Felix Krahmer, Peter Rashkov, David Walnut Publications: 12,20,24,26,27,29,33
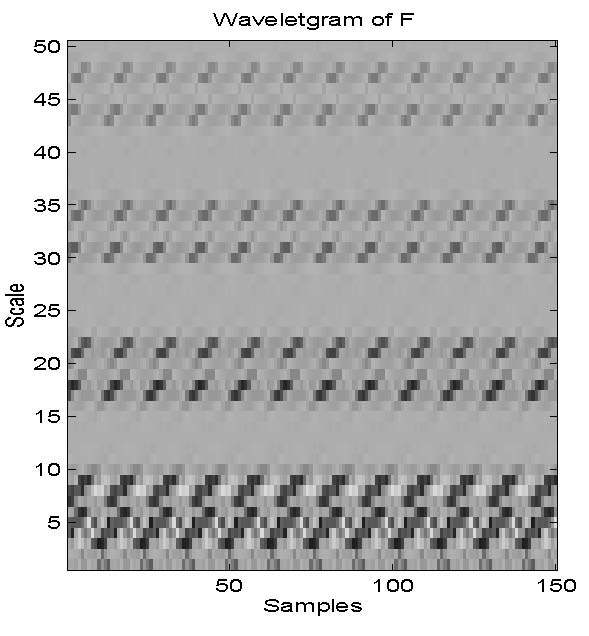
		Wavelet periodicity detection The theory of periodic wavelet transforms developed here is motivated by the problem of epileptic seizure prediction based on the analysis of electrical potential time series derived from brain activity of patients before and during an epileptic seizure. A central theorem in the theory is the characterization of wavelets having time and scale periodic wavelet transforms. We showed that such wavelets are precisely generalized Haar wavelets plus a logarithmic term. This theorem could not only be quantified to analyze seizure prediction, but could also provide a technique to address a large class of periodicity detection problems. An essential step in this quantification is the geometric and linear algebra construction of a generalized Haar wavelet associated with a given periodicity. This gives rise to an algorithm for periodicity detection based on the periodicity of wavelet transforms defined by generalized Haar wavelets and implemented by wavelet averaging methods. The algorithm detects periodicities embedded in significant noise. Collaborators: John Benedetto, Alfredo Nava-Tudela Publications: 0,1,2,3,5,8

• Matlab code: Periodicity detection tools (based on my thesis)
• PerMat - Perturbation Matrices
• Matlab package to compute with functions defined on the integers

Please contact me if you are interested in using these tools!

---