Steuerungstasten

→ nächste Folie (auch Enter oder Spacebar).
← vorherige Folie
 d  schaltet das Zeichnen auf Folien ein/aus
 p  wechselt zwischen Druck- und Präsentationsansicht
CTRL  +  vergrößert die Folien
CTRL  -  verkleinert die Folien
CTRL  0  setzt die Größenänderung zurück

Das Weiterschalten der Folien kann ebenfalls durch das Klicken auf den rechten bzw. linken Folienrand erfolgen.

Notation

Typ Schriftart Beispiele
Variablen (Skalare) kursiv $a, b, x, y$
Funktionen aufrecht $\mathrm{f}, \mathrm{g}(x), \mathrm{max}(x)$
Vektoren fett, Elemente zeilenweise $\mathbf{a}, \mathbf{b}= \begin{pmatrix}x\\y\end{pmatrix} = (x, y)^\top,$ $\mathbf{B}=(x, y, z)^\top$
Matrizen Schreibmaschine $\mathtt{A}, \mathtt{B}= \begin{bmatrix}a & b\\c & d\end{bmatrix}$
Mengen kalligrafisch $\mathcal{A}, B=\{a, b\}, b \in \mathcal{B}$
Zahlenbereiche, Koordinatenräume doppelt gestrichen $\mathbb{N}, \mathbb{Z}, \mathbb{R}^2, \mathbb{R}^3$

Kameras

  • Um eine dreidimensionale Szene als zweidimensionales Bild darzustellen, muss dieser Abbildungsvorgang mathematisch beschrieben werden
  • Der Abbildungsvorgang von 3D-Objekten in eine 2D-Bildebene wird auch häufig Projektion genannt
  • Dazu werden in der Computergrafik verschiedene Kameramodelle verwendet

Kameramodelle

lens_flare
Effekte durch Linsenreflexionen
in der Kamera
  • Oft sind diese Kameramodelle idealisiert und simulieren nur näherungsweise die Effekte, die z.B. beim Betrachten der Welt mit unseren Augen oder mit einer realen Kamera auftreten
  • In dieser einführenden Vorlesung werden nur diejenigen geometischen Projektionen behandelt, die entstehen, wenn gerade Linien als Projektionsstrahlen verwendet werden
Quelle: Alan Weir, Creative Commons License

Kameramodelle

  • Insbesondere lassen sich die Kameramodelle in perspektivische Projektion und Parallelprojektion klassifizieren
perspektivische Projektion
Perspektivische Projektion
Parallelprojektion
Parallelprojektion

Perspektivische Projektion

Lochkamera

  • Die perspektivische Projektion ist uns als Menschen sehr vertraut, da auch unser Auge eine solche perspektivische Projektion vornimmt
  • Ein besonderes Kennzeichen der perspektivischen Projektion, im Gegensatz zur Parallelprojektion, ist, dass Objekte mit größerem Abstand zum Betrachter bzw. Kamera kleiner werden
  • Die einfachste perspektivische Projektion ist die Abbildung mit Hilfe einer Lochkamera

Lochkamera

  • Eine Lochkamera besteht aus einem Kameragehäuse mit einem sehr kleinen Loch durch das das Licht eindringen kann
  • Das Bild formt sich an der Rückseite des Kameragehäuses und steht auf dem Kopf
  • Ein größeres Loch hat den Vorteil, dass mehr Licht in die Kamera eindringen kann, was zu kürzeren Belichtungszeiten führt
  • Der Nachteil ist, dass sich die Projektionen überlagern und das Bild unscharf wird
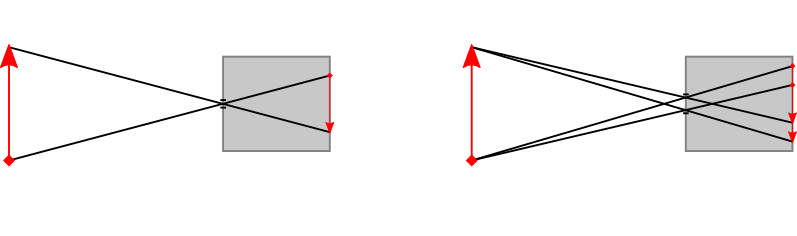
pinhole1
Objekt
Kamera
Loch
Abbildung
des Objekts
Größeres Loch

Lochkamera

  • In der Computergrafik wird meist ein idealisiertes Kameramodell mit einem unendlich kleinen Loch verwendet
  • Dieses Kameramodel kann keine Tiefenunschärfe simulieren, d.h. alle Objekte werden scharf abgebildet
  • Desweitern wird angenommen, dass das Bild auf einer imaginären Bildebene vor dem Projektionszentrum erzeugt wird, sodass das Bild nicht mehr auf dem Kopf steht
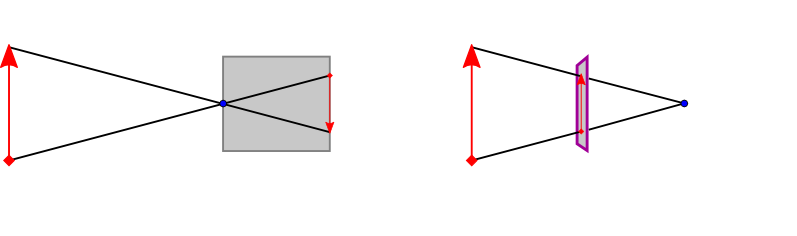
pinhole2
Objekt
Kamera
Loch
Abbildung
des Objekts
Projektionszentrum
Bildebene

Perspektivische Projektion

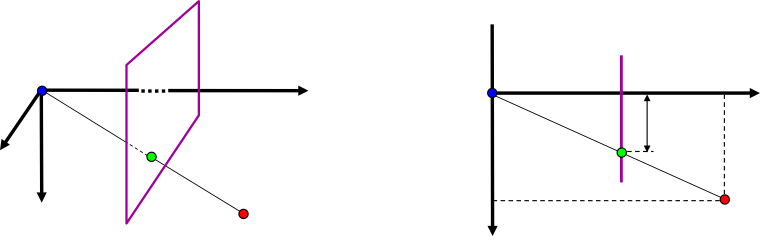
projection
Brennweite
Projektionszentrum
Bildebene
Brennweite
Bildebene
$x$
$y$
$z$
$x$
$f$
$z$
$\tilde{\mathbf{P}}$
$\mathbf{P}$
$\tilde{\mathbf{P}}$
$\mathbf{P}$
$f \frac{p_x}{p_z}$
$f$
  • Die Projektionsvorschrift zur Abbildung eines 3D Punkts $\mathbf{P}=(p_x,p_y,p_z)^\top$ auf einen Punkt $\tilde{\mathbf{P}}= (\tilde{p}_x,\tilde{p}_y,\tilde{p}_z)^\top$ auf der Bildebene der Kamera lautet:

    $\tilde{\mathbf{P}}= \left( f \frac{p_x}{p_z}, f \frac{p_y}{p_z}, f \right)^\top$

  • Dies leitet sich sofort aus der Zeichnung mit Hilfe des Strahlensatzes ab, da

    $\frac{\tilde{p}_x}{f} = \frac{p_x}{p_z}$ und $\frac{\tilde{p}_y}{f} = \frac{p_y}{p_z}$

Perspektivische Projektion

  • Bei Verwendung von homogenen Koordinaten kann die perspektivische Projektion als lineare Abbildung mittels einer $4 \times 4$ Matrix geschrieben werden:

    $\tilde{\mathbf{P}}= \begin{pmatrix} \tilde{p}_x \\ \tilde{p}_y \\ \tilde{p}_z \end{pmatrix}= \begin{pmatrix} f \frac{p_x}{p_z}\\ f \frac{p_y}{p_z}\\ f \end{pmatrix} \in \mathbb{R}^3 \longmapsto \underline{\tilde{\mathbf{P}}}= \begin{pmatrix}f \, p_x \\f \, p_y \\ f \, p_z\\ p_z\end{pmatrix} \in \mathbb{H}^3$

    $\begin{align}\underline{\tilde{\mathbf{P}}} & = \begin{pmatrix}f \, p_x \\f \, p_y \\ f \, p_z\\ p_z\end{pmatrix} = \underbrace{\begin{bmatrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & f & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix}}_{\mathtt{A}} \begin{pmatrix}p_x \\p_y \\ p_z\\ 1\end{pmatrix}\\ \underline{\tilde{\mathbf{P}}} &=\mathtt{A}\, \underline{\mathbf{P}} \end{align}$

Perspektivische Projektion in OpenGL

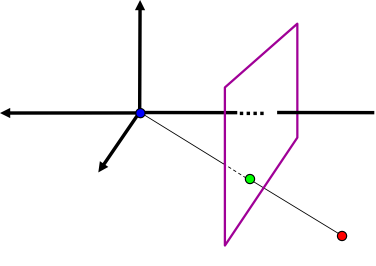
projection_negz
$f$
Bildebene
$x$
$y$
$z$
  • In OpenGL zeigt die Kamera in die negative $z$-Richtung, damit gilt:

    $\begin{align}\underline{\tilde{\mathbf{P}}} & = \begin{pmatrix}f \, p_x \\f \, p_y \\ f \, p_z\\ -p_z\end{pmatrix} = \underbrace{\begin{bmatrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & f & 0 \\ 0 & 0 & -1 & 0 \end{bmatrix}}_{\mathtt{A}} \begin{pmatrix}p_x \\p_y \\ p_z\\ 1\end{pmatrix}\\ \underline{\tilde{\mathbf{P}}} &=\mathtt{A}\, \underline{\mathbf{P}} \end{align}$

Perspektivische Projektion in OpenGL

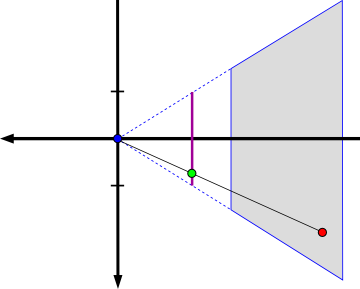
projection_clipping_map
near
far
$x$
$z$
$-z_n$
$-z_f$
dargestellter
Bereich
  • In OpenGL gibt es eine sogenannte Near- und eine Far-Clipping-Ebene
  • Die Near-Ebene und die Far-Ebene verlaufen parallel zur Bildebene
  • Es sollen nur Punkte mit einer $z$-Koordinate dargestellt werden, die innerhalb des von der Near- und der Far-Ebene definierten Bereichs fallen
  • Zu diesem Zweck soll eine neue lineare Abbildung definiert werden, bei der für die $z$-Koordinate der Punkte auf der Near-Ebene gelten soll:

    $p_z=-z_n \quad \mapsto \quad \tilde{p}_z=-1$

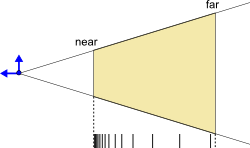
    und für Punkte auf der Far-Ebene:

    $p_z=-z_f \quad \mapsto \quad \tilde{p}_z=1$

  • Um dies zu erreichen, werden zwei neue Parameter $\alpha$ und $\beta$ in die lineare Transformationsmatrix hinzugefügt

Perspektivische Projektion in OpenGL

$\underline{\tilde{\mathbf{P}}} = \begin{pmatrix}f \, p_x \\f \, p_y \\ \alpha \, p_z + \beta \\ -p_z\end{pmatrix} = \begin{bmatrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & \alpha & \beta \\ 0 & 0 & -1 & 0 \end{bmatrix} \begin{pmatrix}p_x \\p_y \\ p_z\\ 1\end{pmatrix} \in \mathbb{H}^3$

  • Für den projizierten Punkt in kartesischen Koordinaten gibt damit:

    $\tilde{\mathbf{P}}=(\tilde{p}_x,\tilde{p}_y,\tilde{p}_z)^\top = \left( f \frac{p_x}{-p_z}, f \frac{p_y}{-p_z}, -\alpha \, + \frac{\beta}{-p_z} \right)^\top \in \mathbb{R}^3$

  • Nun können $\alpha$ und $\beta$ aus den Bedingungen für die Abbildung der $z$-Koordinate bestimmt werden:
    $\begin{align}p_z=-z_n \,&\mapsto \, \tilde{p}_z=-1 \quad \Rightarrow -\alpha \, + \frac{\beta}{z_n} = -1 \\ p_z=-z_f \, &\mapsto \, \tilde{p}_z=\ 1 \,\,\, \,\quad \Rightarrow -\alpha \, + \frac{\beta}{z_f} = 1\end{align}$

Perspektivische Projektion in OpenGL

  • Auflösen des Gleichungssystems nach $\alpha$ und $\beta$ liefert:

    $\begin{align} \alpha &= \frac{z_f+z_n}{z_n-z_f}\\ \beta & = \frac{2 z_f \, z_n}{z_n-z_f}\end{align}$

  • Damit gilt für die neue Projektionsmatrix:

    $\begin{align} \underline{\tilde{\mathbf{P}}} & = \underbrace{\begin{bmatrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & \frac{z_f+z_n}{z_n-z_f} & \frac{2 z_f \, z_n}{z_n-z_f} \\ 0 & 0 & -1 & 0 \end{bmatrix}}_{\mathtt{A}} \begin{pmatrix}p_x \\p_y \\ p_z\\ 1\end{pmatrix}\\ \underline{\tilde{\mathbf{P}}} &=\mathtt{A}\, \underline{\mathbf{P}} \end{align}$

Perspektivische Projektion in OpenGL

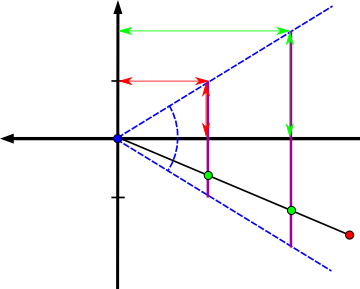
projection_ysize
Brennweite A
Bildhöhe A
Brennweite B
Bildhöhe B
$y$
$z$
1
-1
$\Theta$
  • Bisher haben wir zwar den Abstand der Bildebene zur Kamera durch die Brennweite $f$ definiert, jedoch keine Aussage über die Größe der Bildebene in $x$- und $y$-Richtung getroffen
  • Letztendlich ist nur das Verhältnis zwischen der Größe der Bildebene und der Brennweite entscheidend, das über den Öffnungswinkel $\Theta$ eindeutig definiert ist. Alle Konfigurationen mit dem gleichen Öffnungswinkel resultieren in dem gleichen Bild (nur mit skalierten $x$- und $y$-Koordinaten).
  • In OpenGL wird die Größe der Bildebene daher immer so gewählt, dass die resultierenden $x$- und $y$-Koordinaten im Bereich $[-1; 1]$ liegen.
  • Für einen gegebenen Öffnungswinkel ergibt sich daher für die Brennweite (gemäß Zeichnung):

    $\frac{f}{1} = \frac{\cos( 0.5 \, \Theta)}{\sin( 0.5 \, \Theta)} \Leftrightarrow f = \mathrm{cotan}( 0.5 \, \Theta)$

Transformationsmatrizen in OpenGL

  • Für die Projektion vom Kamerakoordinatensystem in die Bildebene ist die GL_PROJECTION Matrix verantwortlich.
  • Die Manipulation dieser Matrix wird aktiviert durch 
    glMatrixMode(GL_PROJECTION);
  • Alle Funktionen zur Matrixmanipulation, wie glLoadIdentity, glLoadMatrix, glMultMatrix, glRotate, glScale, glTranslate, glPushMatrix, glPopMatrix, gluPerspective werden dann auf der GL_PROJECTION Matrix ausgeführt.
  • Der aktuelle Zustand der GL_PROJECTION Matrix beeinflusst die Transformation der Objekte nur dann, wenn diese gezeichnet werden (OpenGL als Zustandsmaschine)

Perspektivische Projektion in OpenGL

Erzeugen einer perspektivischen Projektionsmatrix in OpenGL:

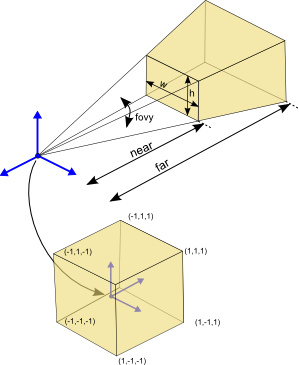
gluperspective
$\mathtt{A}$
$x$
$y$
$z$
$x$
$y$
$z$
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective(fovy, aspect, near, far);

$ \mathtt{A} = \begin{bmatrix} \frac{f}{\mathrm{aspect}} & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & \frac{\mathrm{far}+\mathrm{near}}{\mathrm{near}-\mathrm{far}} & \frac{2 \ast \mathrm{far} \ast \mathrm{near}}{\mathrm{near}-\mathrm{far}} \\ 0 & 0 & -1 & 0 \end{bmatrix}$

mit $f = \mathrm{cotan}( 0.5 \ast \mathrm{fovy})$

und $\mathrm{aspect}= \mathrm{w} / \mathrm{h}$

Beispiel: "Dolly Zoom" oder "Vertigo Effekt"

  • Die Idee des "Dolly Zoom"-Effekts ist, eine Translation der Kamera in $z$-Richtung ("Dolly") durch eine entsprechende Veränderung der Brennweite ("Zoom") auszugleichen
  • Mathematisch ist die Möglichkeit einer Kompensation leicht aus der Projektionsgleichung zu entnehmen, da für die $y$-Koordinate eines projizierten Punkts gilt:

    $\tilde{p}_y = f \frac{p_y}{-p_z}$

  • Da es nur eine Brennweite $f$ gibt aber typischerweise viele 3D-Punkte mit unterschiedlichem Tiefenwert $p_z$ in einer 3D Szene, kann die Kompensation nur für einen bestimmten Tiefenwert gelingen. Es entsteht ein interessanter perspektivischer Effekt.
  • Ein bekannter Film ist Vertigo (1958) von Alfred Hitchcock, der diesen Effekt zur Simulation von Schwindelgefühlen des Protagonisten verwendet hat

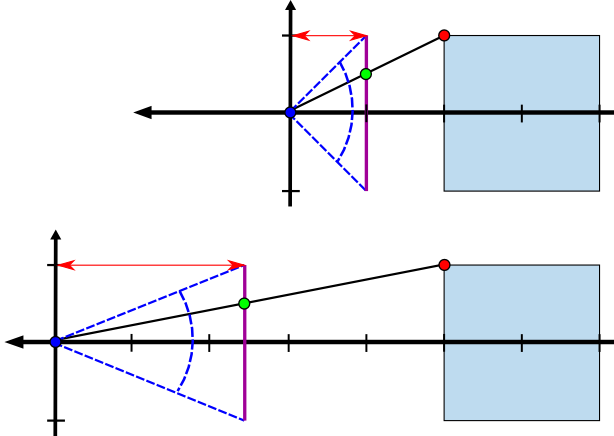
Beispiel: "Dolly Zoom" oder "Vertigo Effekt"

dolly_zoom
Brennweite $f$
$f'$
$y$
$z$
1
-1
$\Theta$
$y$
z
1
-1
$\Theta'$
Objekt
Zeitpunkt $t=t_0=1$
Zeitpunkt $t > 1$
1
2
3
4
$3\,t$
z.B. Einheitswürfel
$\mathbf{P}$
$\mathbf{P}'$

Beispiel: Dolly Zoom in OpenGL

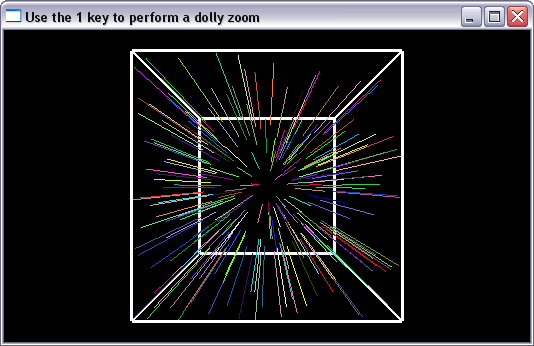
opengl_dollyzoom

Beispiel: Dolly Zoom in OpenGL

class Renderer {

public:
  float t; //time
  const float d0; // initial distance

public:
  Renderer() : t(1.0), d0(3.0), width(0), height(0) {}

public:
  void display() {
    glClearColor(0.0f, 0.0f, 0.0f, 0.0f);
    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

    glMatrixMode(GL_PROJECTION);
    glLoadIdentity();
    gluPerspective (dollyZoomFovy(), 
                    (float)width/(float)height, 
                    0.1, 50.0);

    glMatrixMode(GL_MODELVIEW);
    glLoadIdentity();
    // translate camera by 3 units
    glTranslatef(0.0f, 0.0f, -t*d0);

    // draw a cube in the local coordinate system
    drawCube();
    // draw random lines
    drawRandomLines();
  }

  void init() {
    glEnable(GL_DEPTH_TEST);

    // create random values between -1.0 and 1.0
    for(unsigned r=0; r < 1000; r++) {
      int r = rand();
      randVals.push_back(2.0*float(r)/float(RAND_MAX)-1.0f);
    }
  }

  void resize(int w, int h) {
    // ignore this for now
    glViewport(0, 0, w, h);
    width = w;
    height = h;
  }

  float dollyZoomFovy() {
    float fovyInit = 60.0f; // initial field of view
    float theta = fovyInit / 180.0f * M_PI; // degree to rad
    float f = 1.0f / tan(theta/2.0f);
    float fNew = f * (d0*t-1) / (d0-1);
    float thetaNew = atan(1.0f / fNew) * 2.0f;
    float val = 180.0 * thetaNew / M_PI; //rad to degree
    return val;
  }

private:
  int width;
  int height;
  std::vector<float> randVals;

private:
  void drawCube() {

    glColor3f(1.0f, 1.0f, 1.0f);
    glLineWidth(3.0f);
    glBegin(GL_LINE_LOOP);
    glVertex3f(-1.0f, 1.0f, 1.0f);
    glVertex3f( 1.0f, 1.0f, 1.0f);
    glVertex3f( 1.0f,-1.0f, 1.0f);
    glVertex3f(-1.0f,-1.0f, 1.0f);
    glEnd();
    glBegin(GL_LINE_LOOP);
    glVertex3f(-1.0f, 1.0f,-1.0f);
    glVertex3f( 1.0f, 1.0f,-1.0f);
    glVertex3f( 1.0f,-1.0f,-1.0f);
    glVertex3f(-1.0f,-1.0f,-1.0f);
    glEnd();

    glBegin(GL_LINE_LOOP);
    glVertex3f( 1.0f, 1.0f,-1.0f);
    glVertex3f( 1.0f, 1.0f, 1.0f);
    glVertex3f( 1.0f,-1.0f, 1.0f);
    glVertex3f( 1.0f,-1.0f,-1.0f);
    glEnd();

    glBegin(GL_LINE_LOOP);
    glVertex3f(-1.0f, 1.0f,-1.0f);
    glVertex3f(-1.0f, 1.0f, 1.0f);
    glVertex3f(-1.0f,-1.0f, 1.0f);
    glVertex3f(-1.0f,-1.0f,-1.0f);
    glEnd();
    glLineWidth(1.0);
  }

  void drawRandomLines() {
    if(randVals.size() % 5) return;
    unsigned i = 0;
    while(i < randVals.size()) {
      glColor3f(fabs(randVals[i++]), 
                fabs(randVals[i++]), 
                fabs(randVals[i++]));
      float x = randVals[i++];
      float y = randVals[i++];
      glBegin(GL_LINES);
      glVertex3f(x, y, -1.0f);
      glVertex3f(x, y,  1.0f);
      glEnd();
    }
  }
};

Transformation der Kamera

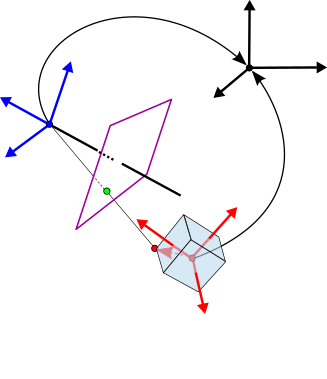
local2cam2
$\mathtt{T}_{\mathrm{\small cam}}$
$\mathtt{T}_{\mathrm{\small obj}}$
Weltkoordinatensystem
Lokales Koordinatensystem
Kamerakoordinatensystem
  • Bisher wurde angenommen, dass sich das Projektionszentrum der Kamera im Ursprung des globalen Weltkoordinatensystems befindet
  • Wird eine Transformation $\mathtt{T}_{\mathrm{\small cam}}$ auf die Kamera angewendet, gilt für die Projektion eines Punkts $\mathbf{P}$ aus einem lokalen Objektkoordinatensystem:

    $\underline{\tilde{\mathbf{P}}} = \mathtt{A} \, \mathtt{T}_{\mathrm{\small cam}}^{-1} \, \mathtt{T}_{\mathrm{\small obj}} \, \underline{\mathbf{P}}$

Transformation der Kamera

Abbildungsvorschrift für homogene Punkte:

$\underline{\tilde{\mathbf{P}}} = \mathtt{A} \, \mathtt{T}_{\mathrm{\small cam}}^{-1} \, \mathtt{T}_{\mathrm{\small obj}} \, \underline{\mathbf{P}}$

Dabei beschreibt die $4 \times 4$ Matrix

  • $\mathtt{T}_{\mathrm{\small obj}}$ die Transformation vom lokalen Koordinatensystem ins Weltkoordinatensystem
  • $\mathtt{T}_{\mathrm{\small cam}}^{-1}$ die Transformation vom Weltkoordinatensystem ins Kamerakoordinatensystem
  • $\mathtt{A}$ die Transformation vom Kamerakoordinatensystem in die Bildebene

Transformation der Kamera

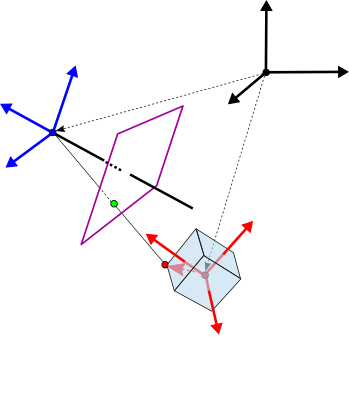
local2cam2
$\mathbf{C}_a$
$\mathbf{C}_b$
$\mathbf{e}_x$
$\mathbf{e}_y$
$\mathbf{e}_z$
$\tilde{\mathbf{a}}_x$
$\tilde{\mathbf{a}}_y$
$\tilde{\mathbf{a}}_z$
$\tilde{\mathbf{b}}_x$
$\tilde{\mathbf{b}}_y$
$\tilde{\mathbf{b}}_z$
Weltkoordinatensystem
Lokales Koordinatensystem
Kamerakoordinatensystem
  • Die Transformationsmatrizen ergeben sich durch Betrachten der Basisvektoren der Koordinatensysteme (wie in den vorherigen Kapiteln besprochen)
  • Die Transformationsmatrix $\mathtt{T}_{\mathrm{\small obj}}$ transformiert einen Punkt vom lokalen ins Weltkoordinatensystem

    $ \mathtt{T}_{\mathrm{\small obj}} = \begin{bmatrix}\tilde{\mathbf{b}}_x & \tilde{\mathbf{b}}_y & \tilde{\mathbf{b}}_z & \mathbf{C}_b\\0 & 0 & 0 & 1\end{bmatrix}$

  • Die Transformationsmatrix $\mathtt{T}_{\mathrm{\small cam}}$ tranformiert einen Punkt vom Kamera- ins Weltkoordinatensystem

    $\begin{align} \mathtt{T}_{\mathrm{\small cam}} & = \begin{bmatrix}\tilde{\mathbf{a}}_x & \tilde{\mathbf{a}}_y & \tilde{\mathbf{a}}_z & \mathbf{C}_a\\0 & 0 & 0 & 1\end{bmatrix} \\ & = \begin{bmatrix} \mathtt{R}_a & \mathbf{C}_a\\ \mathbf{0}^\top & 1\end{bmatrix} \end{align}$

Transformation der Kamera

  • Für die inverse Transformation $\mathtt{T}_{\mathrm{\small cam}}^{-1}$ vom Welt- ins Kamerakoordinatensystem, ergibt sich mit $ \mathtt{R}_a^{-1}= \mathtt{R}_a^\top$:

    $\mathtt{T}_{\mathrm{\small cam}}^{-1} = \begin{bmatrix} \mathtt{R}_a & \mathbf{C}_a\\ \mathbf{0}^\top & 1\end{bmatrix}^{-1} = \begin{bmatrix} \mathtt{R}_a^{\top} & -\mathtt{R}_a^{\top} \mathbf{C}_a\\ \mathbf{0}^\top & 1\end{bmatrix} $

Transformation der Kamera in OpenGL

Abbildungsvorschrift für homogene Punkte:

$\underline{\tilde{\mathbf{P}}} = \mathtt{A} \, \underbrace{\mathtt{T}_{\mathrm{\small cam}}^{-1} \, \mathtt{T}_{\mathrm{\small obj}}}_{\mathtt{T}_{\mathrm{\small modelview}}} \, \underline{\mathbf{P}}$

  • In OpenGL werden alle Transformationen außer der Projektionsmatrix $\mathtt{A}$ zu einer so genannten GL_MODELVIEW Matrix zusammengefasst
  • Die GL_MODELVIEW Matrix beschreibt somit direkt die Transformation vom jeweiligen lokalen Koordinatensystem ins Kamerakoordinatensystem
  • Die GL_PROJECTION Matrix $\mathtt{A}$ beschreibt die Abbildung vom Kamerakoordinatensystem in die Bildebene

gluLookAt

  • Zur einfachen Definition der Matrix $\mathtt{T}_{\mathrm{\small cam}}^{-1}$ existiert die GLU-Funktion 
    gluLookAt(eyex, eyey, eyez, refx, refy, refz, upx, upy, upz);
  • Durch Definition eines Augpunkts $\mathbf{C}_{\mathrm{\small eye}}$, eines anvisierten Referenzpunkts $\mathbf{P}_{\mathrm{\small ref}}$ und eines Vektors $\mathbf{v}_{\mathrm{\small up}}$ (der definiert, in welche Richtung die $y$-Koordinate der Kamera zeigt) ergeben sich die Basisvektoren des Kamerakoordinatensystems zu:
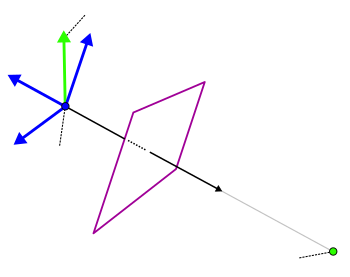
    lookat
    Augpunkt $\mathbf{C}_{\mathrm{\small eye}}$
    Referenzpunkt $\mathbf{P}_{\mathrm{\small ref}}$
    Up-Vektor $\mathbf{v}_{\mathrm{\small up}}$
    $\tilde{\mathbf{a}}_x$
    $\tilde{\mathbf{a}}_y$
    $\tilde{\mathbf{a}}_z$

    $\begin{align} \mathbf{d} & = \mathbf{C}_{\mathrm{\small eye}} - \mathbf{P}_{\mathrm{\small ref}}\\ \tilde{\mathbf{a}}_z &= \frac{\mathbf{d}}{|\mathbf{d}|}, \mathbf{v}' = \frac{\mathbf{v}_{\mathrm{\small up}}}{|\mathbf{v}_{\mathrm{\small up}}|} \\ \tilde{\mathbf{a}}_x &= \mathbf{v}'\times \tilde{\mathbf{a}}_z \\ \tilde{\mathbf{a}}_y &= \tilde{\mathbf{a}}_z \times \tilde{\mathbf{a}}_x\\ \mathtt{R}_{a} & = \begin{bmatrix}\tilde{\mathbf{a}}_x & \tilde{\mathbf{a}}_y & \tilde{\mathbf{a}}_z \end{bmatrix} \\ \end{align}$

    Damit gilt:
    $\mathtt{T}_{\mathrm{\small cam}}^{-1} = \begin{bmatrix} \mathtt{R}_a^{\top} & -\mathtt{R}_a^{\top} \mathbf{C}_{\mathrm{\small eye}}\\ \mathbf{0}^\top & 1\end{bmatrix}$

Beispiel: gluLookAt

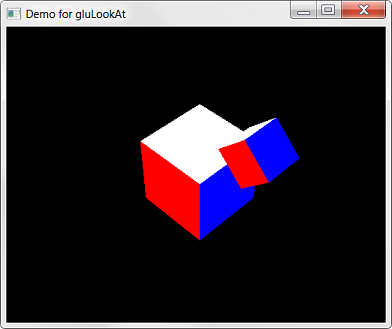
opengl_glulookatsimple

Beispiel: gluLookAt

class Renderer {
  ...
  void resize(int w, int h) {
    glViewport(0, 0, w, h);
    glMatrixMode(GL_PROJECTION);
    glLoadIdentity();
    gluPerspective (30.0, (float)w/(float)h, 2.0, 20.0);
  }
  void display() {    
    glClearColor(0.0f, 0.0f, 0.0f, 0.0f);
    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
    glMatrixMode(GL_MODELVIEW);
    glLoadIdentity();

    // camera orbits in the y=10 plane
    // and looks at origin
    double rad = M_PI / 180.0f * t;
    gluLookAt(10.0*cos(rad), 10.0 , 10.0*sin(rad), // eye
              0.0, 0.0, 0.0, // look at
              0.0, 1.0, 0.0); // up

    //draw cube at origin
    drawCube();

    glRotatef(45.0f, 0.0f, 0.0f, 1.0f);
    glTranslatef(2.5f, 0.0f, 0.0f );
    glScalef(0.5f, 0.5f, 0.5f);

    //draw transformed cube
    drawCube(); 
  }
  ...
}

Beispiel: gluLookAt

  • Welche Transformationen durchlaufen die Punkte des kleineren Würfels? 
    glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective (...);

glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
gluLookAt(...);


glRotatef(...);
glTranslatef(...);
glScalef(...);

    $\mathtt{T}_{\mathrm{\small projection}}= \mathtt{I}$
    $\mathtt{T}_{\mathrm{\small projection}}= \mathtt{I} \, \mathtt{A}$

    $\mathtt{T}_{\mathrm{\small modelview}}= \mathtt{I}$
    $\mathtt{T}_{\mathrm{\small modelview}}= \mathtt{I}\,\mathtt{T}_{\mathrm{\small cam}}^{-1}$

    $\mathtt{T}_{\mathrm{\small modelview}}= \mathtt{I}\,\mathtt{T}_{\mathrm{\small cam}}^{-1} \,\mathtt{T}_r$
    $\mathtt{T}_{\mathrm{\small modelview}}= \mathtt{I}\,\mathtt{T}_{\mathrm{\small cam}}^{-1} \,\mathtt{T}_r\,\mathtt{T}_t$
    $\mathtt{T}_{\mathrm{\small modelview}}= \mathtt{I}\,\mathtt{T}_{\mathrm{\small cam}}^{-1} \,\mathtt{T}_r\,\mathtt{T}_t\,\mathtt{T}_s $

    $\begin{align} \underline{\tilde{\mathbf{P}}} &= \mathtt{T}_{\mathrm{\small projection}} \mathtt{T}_{\mathrm{\small modelview}} \, \underline{\mathbf{P}}\\ &= \mathtt{A} \, \mathtt{T}_{\mathrm{\small cam}}^{-1} \,\mathtt{T}_r\,\mathtt{T}_t\,\mathtt{T}_s \,\underline{\mathbf{P}} \end{align}$

Beispiel: gluLookAt und Ketten von Transformationen

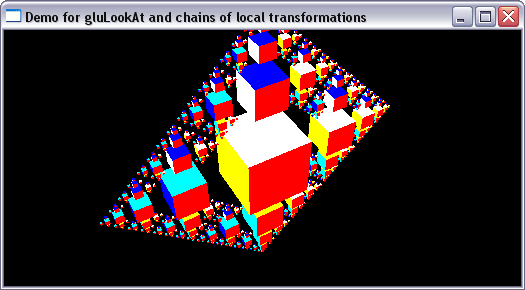
opengl_glulookat

Beispiel: gluLookAt und Ketten von Transformationen

class Renderer {
public:
  float t;

public:
  Renderer() : t(0.0) {}

public:
  void display() {    
    glClearColor(0.0f, 0.0f, 0.0f, 0.0f);
    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

    glMatrixMode(GL_MODELVIEW);
    glLoadIdentity();
    
    // camera orbits in the y=10 plane
    // and looks at origin
    double rad = M_PI / 180.0f * t;
    gluLookAt(10.0*cos(rad), 10.0 , 10.0*sin(rad), // eye
              0.0, 0.0, 0.0, // look at
              0.0, 1.0, 0.0); // up

    //draw model at origin
    drawCubeHierarchy(0, 4);
  }

  void init() {
    glEnable(GL_DEPTH_TEST);
  }

  void resize(int w, int h) {
    glViewport(0, 0, w, h);
    glMatrixMode(GL_PROJECTION);
    glLoadIdentity();
    gluPerspective (30.0, (float)w/(float)h, 0.1, 50.0);
  }

private:
  void drawCube() {
    ...
  }

  void drawCubeHierarchy(int depth, int neighbors) {
    drawCube(); // draw parent
    depth +=1;
    if (depth < 6){
      for (int n = 0; n < neighbors; n++){
        glPushMatrix();
        glRotatef(n*90.0f-90.0f, 0.0f, 0.0f, 1.0f);
        glTranslatef(2.5f, 0.0f, 0.0f );
        glScalef(0.5f, 0.5f, 0.5f);
        drawCubeHierarchy(depth, 3); // draw children
        glPopMatrix();
      }
    }
  }
};

Per-Vertex Operations

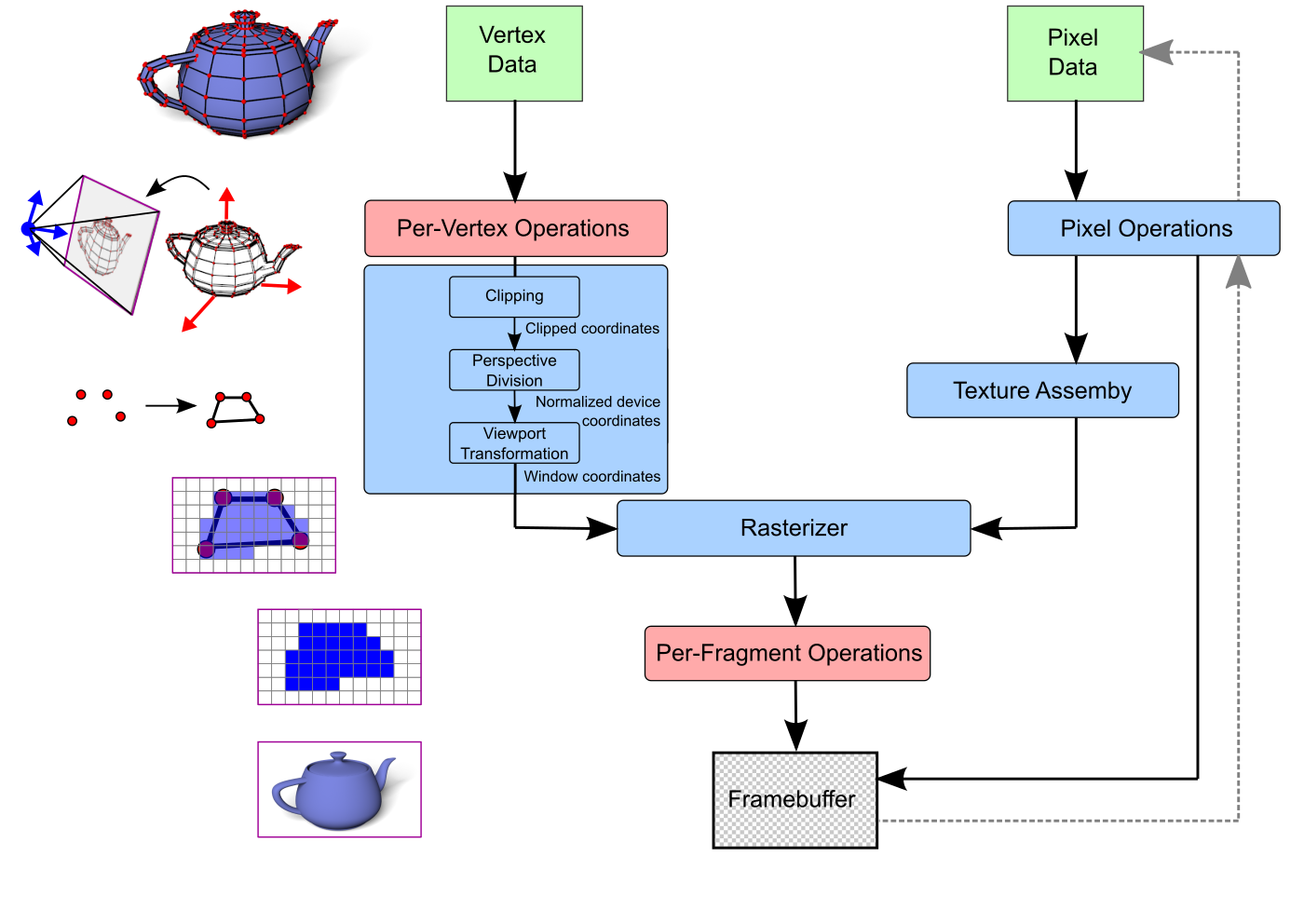
Bei Verwendung der Fixed-Function-Pipeline werden folgende Transformationen auf die Vertex Daten angewendet

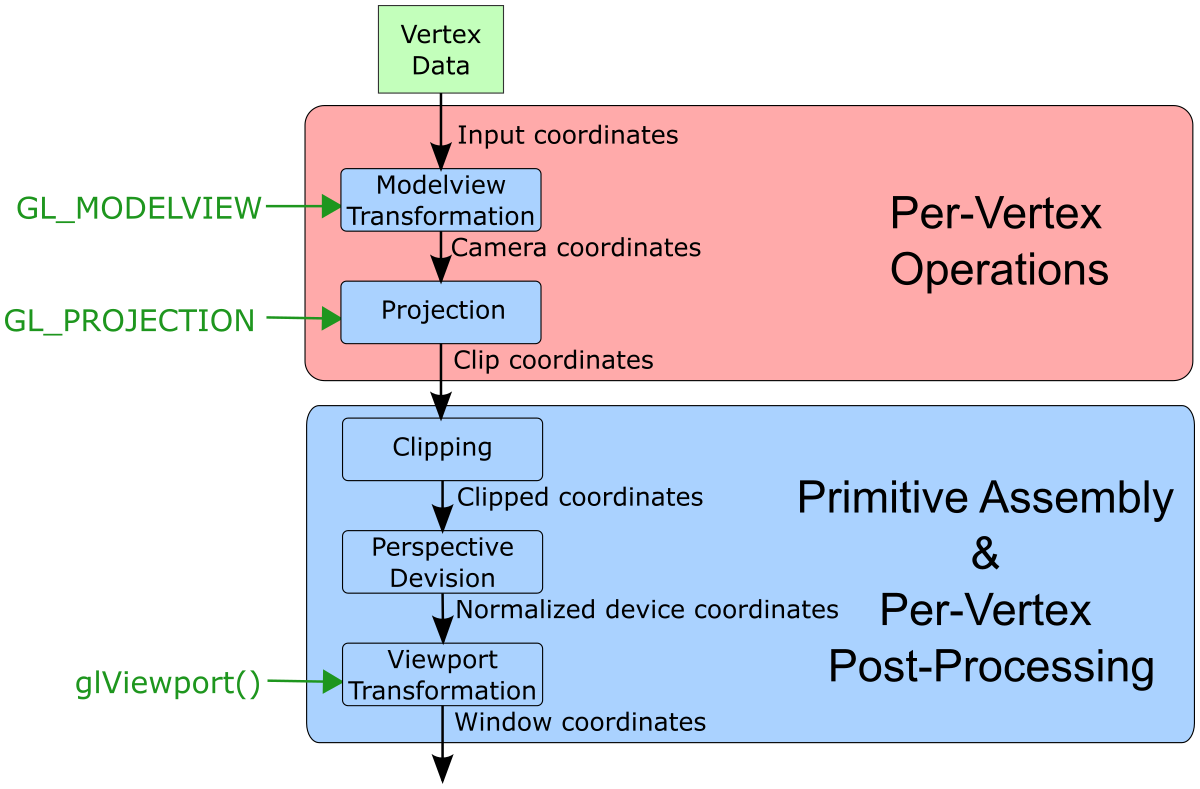
pervertex_fixedfunction_pipeline

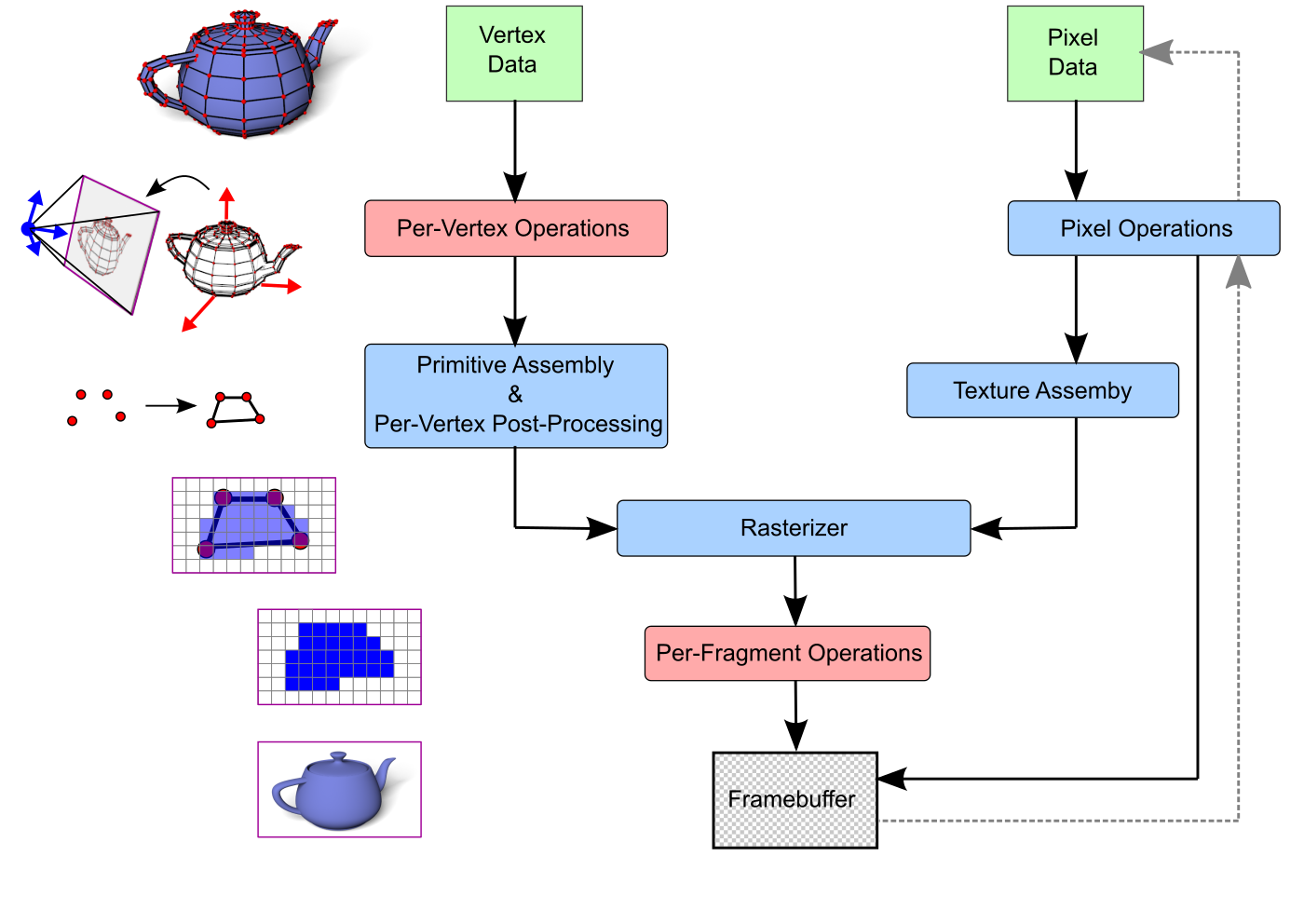
OpenGL-Pipeline

openglpipeline
openglpipeline

Perspektivische Division

  • Die so genannte "perspektivische Division" überführt die projizierten Punkte in homogenen Koordinaten ins kartesische Koordinatensystem durch Division mit der letzte Koordinate:

    $\underline{\mathbf{P}} = \begin{pmatrix}p_x\\p_y\\p_z\\p_w\end{pmatrix} \in \mathbb{H}^3 \quad \longmapsto \quad \mathbf{P}= \begin{pmatrix}\frac{p_x}{p_w}\\\frac{p_y}{p_w}\\\frac{p_z}{p_w} \end{pmatrix} \in \mathbb{R}^3 $

Clipping

  • Die Projektionsmatrix wurde so konstruiert, dass nach Projektion und der perspektivischen Division alle $x$, $y$ und $z$-Koordinaten innerhalb des sichtbaren Volumens auf den Bereich von $-1$ bis $1$ abgebildet werden
  • Alle Primitiven, die vollständig außerhalb diese Bereichs liegen, müssen nicht gezeichnet werden
  • Durch Prüfen auf den Bereich $[-1;1]$ wäre es leicht, das Clipping nach der perspektivischen Division durchzuführen
  • In OpenGL wird das Clipping jedoch vor der perspektivischen Division durchgeführt. Warum?
  • Anstatt auf den Bereich $[-1;1]$ zu prüfen, kann genau so schnell auf den Bereich $[-p_w;p_w]$ geprüft werden

    $-p_w < p_x < p_w \quad \longmapsto \quad -1 < \frac{p_x}{p_w} < 1$

  • Dies hat den Vorteil, dass
    • für den Fall $p_w=0$ keine besondere Behandlung benötigt wird und
    • die Division für die geclippten Koordinaten nicht mehr durchgeführt werden muss

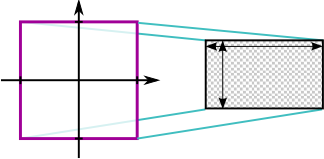
Viewport Transformation

viewport_transformation
$x$
$y$
1
-1
1
-1
Bildschirm
Breite
Höhe
  • Im letzten Transformationsschritt werden die Koordinaten im Bereich $[-1;1]$ auf Bildschirmkoordinaten skaliert
  • Dazu existiert in OpenGL der Befehl
    glViewport(int ix, int iy, int width, int height)
  • Dabei geben ix und iy die linke untere Ecke des Viewports und width und height die Größe an (jeweils in der Einheit Pixel)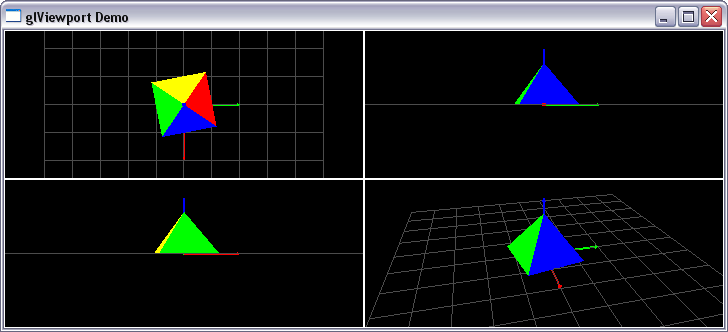

Beispiel: glViewport

opengl_viewport

Beispiel: glViewport

class Renderer {

public:
  float t;

public:
  Renderer() : t(0.0), width(0), height(0) {}

public:
  void display() {
    glClearColor(0.0f, 0.0f, 0.0f, 0.0f);
    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

    // top right viewport (look from front)
    glViewport(width/2, height/2, width/2, height/2);
    glMatrixMode(GL_MODELVIEW);
    glLoadIdentity();
    drawFrame();
    // set camera (look from positive x-direction)
    gluLookAt(10.0, 0.0, 0.0, 
               0.0, 0.0, 0.0, 
               0.0, 0.0, 1.0);
    // draw scene
    drawSceneGrid();
    drawRotatingPyramid();

    // bottom left viewport (look from left)
    glViewport(0, 0, width/2, height/2);
    glMatrixMode(GL_MODELVIEW);
    glLoadIdentity();
    drawFrame();
     // set camera (look from negative y-direction)
    gluLookAt(0.0, -10.0, 0.0, 
              0.0,   0.0, 0.0,
              0.0,   0.0, 1.0);
    // draw scene
    drawSceneGrid();
    drawRotatingPyramid();

    // top left viewport (look from top)
    glViewport(0, height/2, width/2, height/2);
    glMatrixMode(GL_MODELVIEW);
    glLoadIdentity();
    drawFrame();
    // set camera (look from positive z-direction)
     gluLookAt(0.0, 0.0, 10.0, 
               0.0, 0.0,  0.0, 
              -1.0, 0.0,  0.0);
    // draw scene
    drawSceneGrid();
    drawRotatingPyramid();

    // bottom right viewport (perspective)
    glViewport(width/2, 0, width/2, height/2);
    glMatrixMode(GL_MODELVIEW);
    glLoadIdentity();
    drawFrame();
    // set camera
    gluLookAt(8.0, -2.0, 5.0, 
              0.0,  0.0, 0.0, 
              0.0,  0.0, 1.0);
    // draw scene
    drawSceneGrid();
    drawRotatingPyramid();
  }

  void init() {
    glEnable(GL_DEPTH_TEST);
    //glEnable(GL_CULL_FACE);
  }

  void resize(int w, int h) {
    width = w;
    height = h;
    glMatrixMode(GL_PROJECTION);
    glLoadIdentity();
    gluPerspective (30.0, 
                    (float)width/(float)height, 
                    0.1, 50.0);
  }

private:
  int width;
  int height;

private:
  void drawFrame() {
      glLineWidth(2.0);
      glMatrixMode(GL_PROJECTION);
      glPushMatrix();
      glLoadIdentity();
      glColor3f(1.0f, 1.0f, 1.0f);
      glBegin(GL_LINE_LOOP);
      glVertex3f(-1.0f, 1.0f, 0.0f);
      glVertex3f( 1.0f, 1.0f, 0.0f);
      glVertex3f( 1.0f,-1.0f, 0.0f);
      glVertex3f(-1.0f,-1.0f, 0.0f);
      glEnd();
      glPopMatrix();
      glMatrixMode(GL_MODELVIEW);
      glLineWidth(1.0);
  }

  void drawSceneGrid() {
      glColor3f(0.3f, 0.3f, 0.3f);
      glBegin(GL_LINES);
      for(unsigned i=0; i<=10; i++) {
        glVertex3f(-5.0f+i, -5.0f,   0.0f);
        glVertex3f(-5.0f+i,  5.0f,   0.0f);
        glVertex3f(-5.0f,   -5.0f+i, 0.0f);
        glVertex3f( 5.0f,   -5.0f+i, 0.0f);
      }
      glEnd();  

    glColor3f(0.0f, 0.0f, 1.0f);
    drawCoordinateAxisZ();
    glColor3f(0.0f, 1.0f, 0.0f);
    drawCoordinateAxisY();
    glColor3f(1.0f, 0.0f, 0.0f);
    drawCoordinateAxisX();
  }

  void drawCoordinateAxisZ() {
    glLineWidth(2.0);
    glBegin(GL_LINES);
    glVertex3f(0.0f, 0.0f, 0.0f); // z-axis
    glVertex3f(0.0f, 0.0f, 2.0f);
    glEnd();
    glLineWidth(1.0);

    // z-axis tip
    glBegin(GL_TRIANGLES);
    glVertex3f( 0.0f, 0.0f, 2.0f);
    glVertex3f(-0.05f, 0.05f, 1.9f);
    glVertex3f( 0.05f, 0.05f, 1.9f);
    glVertex3f( 0.0f,  0.0f, 2.0f);
    glVertex3f( 0.05f, -0.05f, 1.9f);
    glVertex3f(-0.05f, -0.05f, 1.9f);
    glVertex3f( 0.0f,  0.0f, 2.0f);
    glVertex3f( 0.05f,  0.05f, 1.9f);
    glVertex3f( 0.05f, -0.05f, 1.9f);
    glVertex3f( 0.0f,  0.0f, 2.0f);
    glVertex3f(-0.05f, -0.05f, 1.9f);
    glVertex3f(-0.05f,  0.05f, 1.9f);
    glEnd();
    glBegin(GL_POLYGON);
    glVertex3f( 0.05f, -0.05f, 1.9f);
    glVertex3f( 0.05f,  0.05f, 1.9f);
    glVertex3f(-0.05f,  0.05f, 1.9f);
    glVertex3f(-0.05f, -0.05f, 1.9f);
    glEnd();
  }

  void drawCoordinateAxisX() {
      glPushMatrix();
      glRotatef(90.0f, 0.0f, 1.0f, 0.0f);
      drawCoordinateAxisZ();
      glPopMatrix();
  }

  void drawCoordinateAxisY() {
      glPushMatrix();
      glRotatef(-90.0f, 1.0f, 0.0f, 0.0f);
      drawCoordinateAxisZ();
      glPopMatrix();
  }

  void drawRotatingPyramid() {
    glRotatef(t, 0.0f, 0.0f, 1.0f);
    drawPyramid();
  }

  void drawPyramid() {
    glColor3f(1.0,0.0,0.0);
    glBegin(GL_TRIANGLES);
    glVertex3f( 0.0f, 0.0f, 1.5f);
    glVertex3f(-1.0f, 1.0f, 0.0f);
    glVertex3f( 1.0f, 1.0f, 0.0f);
    glEnd();
    glColor3f(0.0,1.0,0.0);
    glBegin(GL_TRIANGLES);
    glVertex3f( 0.0f,  0.0f, 1.5f);
    glVertex3f( 1.0f, -1.0f, 0.0f);
    glVertex3f(-1.0f, -1.0f, 0.0f);
    glEnd();
    glColor3f(0.0,0.0,1.0);
    glBegin(GL_TRIANGLES);
    glVertex3f( 0.0f,  0.0f, 1.5f);
    glVertex3f( 1.0f,  1.0f, 0.0f);
    glVertex3f( 1.0f, -1.0f, 0.0f);
    glEnd();
    glColor3f(1.0,1.0,0.0);
    glBegin(GL_TRIANGLES);
    glVertex3f( 0.0f,  0.0f, 1.5f);
    glVertex3f(-1.0f, -1.0f, 0.0f);
    glVertex3f(-1.0f,  1.0f, 0.0f);
    glEnd();
    glColor3f(0.0,1.0,1.0);
    glBegin(GL_POLYGON);
    glVertex3f( 1.0f, -1.0f, 0.0f);
    glVertex3f( 1.0f,  1.0f, 0.0f);
    glVertex3f(-1.0f,  1.0f, 0.0f);
    glVertex3f(-1.0f, -1.0f, 0.0f);
    glEnd();
  }
};

Fluchtpunkte

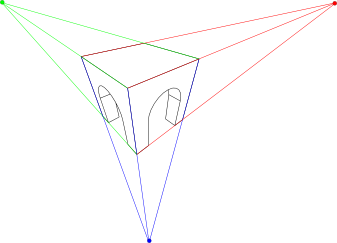
vanishing_points
  • Durch eine perspektivische Abbildung werden parallele Geraden im 3D Raum auf nicht parallele Geraden in der 2D Bildebene abgebildet
  • Der 2D Schnittpunkt dieser Geraden in der Bildebene wird Fluchtpunkt genannt
  • Jede Raumrichtung kann ihren eigenen (oder keinen) Fluchtpunkt besitzen
  • Je nachdem, wie viele Fluchtpunkte existieren, wird die Projektion als 1-, 2- oder 3-Punktperspektive bezeichnet
Quelle: wikipedia.org; Urheber: Wolfram Gothe 2009; gemeinfreies Werk

Z-Buffer

Tiefentest

depthtest_example
  • In den vorherigen Beispielen wurden glEnable(GL_DEPTH_TEST) und glClear(GL_DEPTH_BUFFER_BIT) verwendet, ohne dass deren Funktion diskutiert wurde.
  • Der Aufruf glEnable(GL_DEPTH_TEST) dient dazu, den Tiefentest in OpenGL zu aktivierten
  • Bei deaktiviertem Tiefentest werden die Primitiven in der Reihenfolge in den Framebuffer geschrieben, in der sie die OpenGL-Pipeline durchlaufen.
  • Das heißt, später gezeichnete Primitive werden früher gezeichnete überdecken
  • Das ist typischerweise nicht das gewünschte Verhalten
  • Stattdessen sollen Primitive, die aus Sicht der Kamera näher liegen weiter entfernte verdecken und zwar unabhängig von der Reihenfolge des Zeichnens
  • Idealerweise sollte die Entscheidung pro gezeichnetem Pixel im Framebuffer erfolgen, da sich die einzelnen Primitive durchdringen können
  • In OpenGL wird als Tiefentest das Z-Buffer-Verfahren verwendet

Z-Buffer-Verfahren

gluperspective
$x$
Normalized device coordinates
Camera coordinates
$\mathtt{A}$
$x$
$y$
$z$
$x$
$y$
$z$
  • Obwohl eigentlich die $z$-Koordinate im Kamerakoordinatensystem entscheidend ist, kann der Tiefentest auch noch nach der perspektivischen Division durchgeführt werden, da die Tiefenrelationen erhalten bleiben
  • Wenn "Normalized device coordinates" verwendet werden, dreht sich allerdings bezüglich des Kamerakoordinatensystems die $z$-Achse um, d.h. weiter entfernte Punkte haben ein größeres $z$ (speziell ist dabei das ausnahmsweise linkshändige Koordinatensystem)
  • Für Punkte, die im Kamerakoordinatensystem auf der Near-Ebene lagen, gilt nun $\tilde{p}_z=-1$ bzw. auf der Far-Ebene gilt $\tilde{p}_z=1$

Z-Buffer-Verfahren

  • Das Z-Buffer-Verfahren benötigt, neben dem normalen Framebuffer, der die Farbinformation aufnimmt, einen Depth-Buffer der gleichen Größe, der die Tiefenwerte aufnimmt
frame_vs_depthbuffer
Framebuffer        Depth Buffer

Z-Buffer-Verfahren

  • Zu Beginn des Rendervorgangs wird der Depth-Buffer mit dem z-Werte der Far-Ebene initialisiert. Dazu dient in OpenGL der Befehl glClear(GL_DEPTH_BUFFER_BIT)
  • Das Schreiben eines Pixels in den Frame- und Depth-Buffer geschieht während der Per-Fragment Operationen in der OpenGL-Pipeline.
  • Der Tiefenwert für jedes Pixel wird vom Rasterisierer aus den transformierten Vertex-Daten interpoliert.
  • Ist der Tiefenwert für das Pixel kleiner als der aktuell im Depth-Buffer gespeicherte, wird der Farbwert in den Framebuffer und der Tiefenwert in den Depth-Buffer geschrieben, ansonsten bleiben beide unverändert
FOR each primitiv
  FOR each pixel of primitive at position (x,y) with colour c and depth d
    IF d < depthbuffer(x,y) 
      framebuffer(x,y) = c
      depthbuffer(x,y) = d
    END IF
  END FOR
END FOR

Z-Fighting

depthbuffer_resolution.png
Tiefenauflösung
$z$
  • Der Depth-Buffer hat nur eine bestimmte Genauigkeit. Tpyischerweise ganzahlige Wert mit 16, 24 oder 32 Bit Genauigkeit
  • Das Intervall [-1.0; 1.0] wird auf [0.0, 1.0] abgebildet und dann auf [0, MAX_INT], z.B. [0, 65535] bei 16 Bit
  • Dabei wird auf den nächsten ganzzahligen Wert gerundet
  • Da bei den "Normalized device coordinates" bereits durch $p_w$ geteilt wurde, sind die Rundungsfehler für Objekte nah an der Kamera damit kleiner (und deren Tiefengenauigkeit damit größer)
  • Daher kommt es bei weit entfernten Primitiven, die dort nah beieinander liegen, gelegentlich zum so genanntem "Z-Fighting", da durch die Ungenauigkeiten in den z-Werten zufällig mal das eine, mal das andere, einen kleineren z-Wert hat und dargestellt wird
  • Um Z-Fighting zu beheben, ist es wichtig, die Near- und Far-Ebene möglichst geschickt zu wählen, da diese letztendlich den z-Bereich definieren, auf die sich die möglichen ganzzahligen Tiefenwert verteilen
  • Daher sollte die Near- und Far-Ebene möglichst dicht beieinander gewählt werden, so dass diese die darzustellende 3D-Szene gerade noch komplett umschließen

Beispiel: Z-Fighting

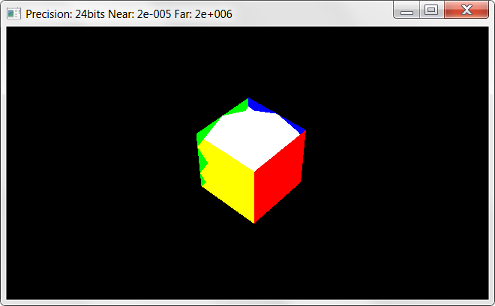
opengl_zfighting

Beispiel: Z-Fighting

class Renderer {

public:
  float t;
  int width, height;
  double nearPlane, farPlane;
  int depthBits; 

public:
  Renderer() : t(0.0), nearPlane(2.0), farPlane(20.0) {}

public:

  void resize(int w, int h) {
    glViewport(0, 0, w, h);
    width = w;
    height = h;
  }

  void display() {    
    glClearColor(0.0f, 0.0f, 0.0f, 0.0f);
    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

    glMatrixMode(GL_PROJECTION);
    glLoadIdentity();
    gluPerspective (30.0, (float)width/(float)height, nearPlane, farPlane);
    glMatrixMode(GL_MODELVIEW);
    glLoadIdentity();

    // camera orbits in the y=10 plane
    // and looks at origin
    double rad = M_PI / 180.0f * t;
    gluLookAt(10.0*cos(rad), 10.0 , 10.0*sin(rad), // eye
              0.0, 0.0, 0.0, // look at
              0.0, 1.0, 0.0); // up

    //draw cube at origin
    drawCube();
  }

  void init() {
    glEnable(GL_DEPTH_TEST);
    glGetIntegerv (GL_DEPTH_BITS, &depthBits);
  }
private:
  void drawCube() {
    ...
  }
};

Gibt es Fragen?

questions

Anregungen oder Verbesserungsvorschläge können auch gerne per E-mail an mich gesendet werden: Kontakt

Weitere Vorlesungsfolien

Folien auf Englisch (Slides in English)

Impressum, Datenschutz,