Multimediale Signalverarbeitung
Faltung und Impulsantwort
Thorsten Thormählen
29. April 2024
Teil 3, Kapitel 1
Thorsten Thormählen
29. April 2024
Teil 3, Kapitel 1
Dies ist die Druck-Ansicht.
Weiterschalten der Folien durch die → Taste oder
durch das Klicken auf
den rechten Folienrand.
Das Weiterschalten der Folien kann ebenfalls durch das Klicken auf den rechten bzw. linken Folienrand erfolgen.
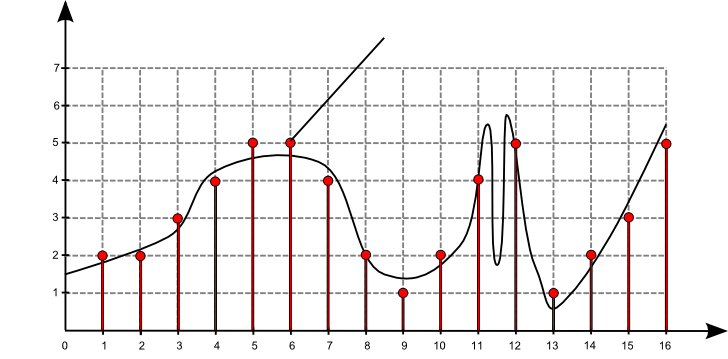

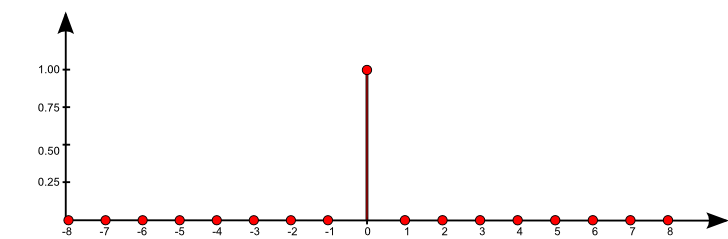
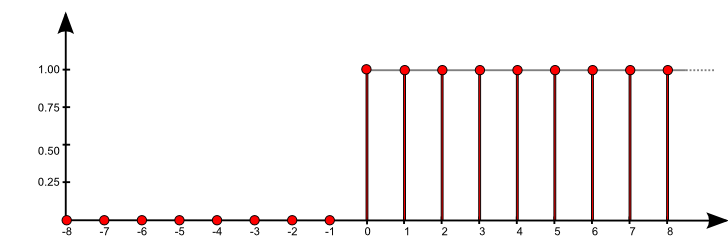
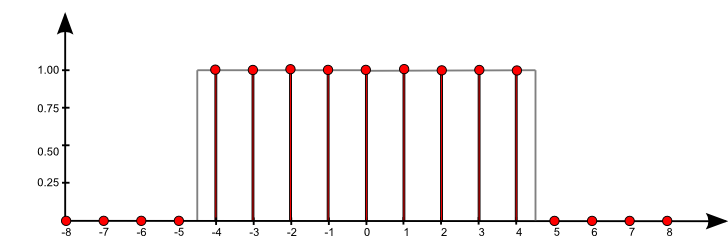
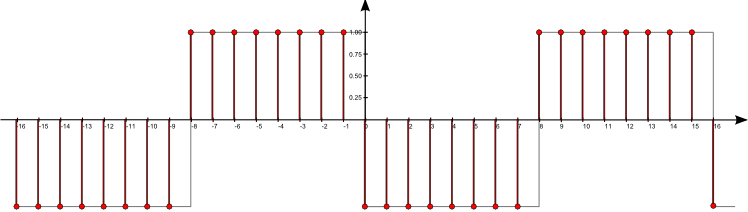
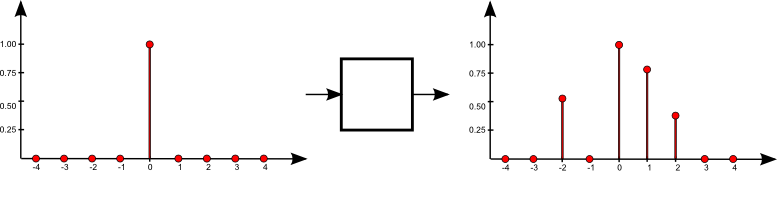
$\mathrm{f}[n] = \sum\limits_{k = -\infty}^{\infty} \mathrm{a}[k] \, \,\mathrm{b}[n-k]$
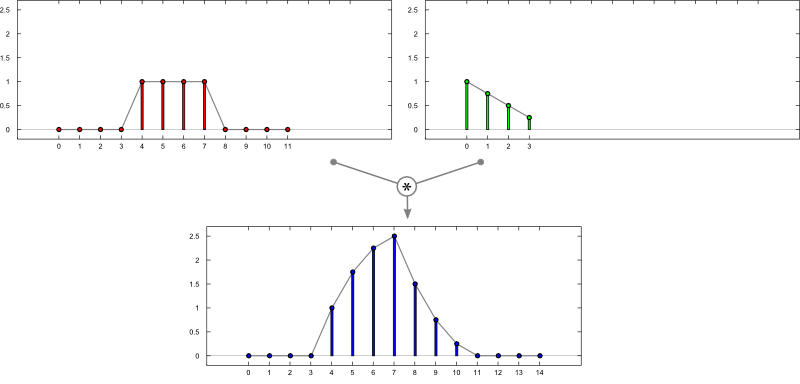
$\mathrm{f}[n] = \sum\limits_{k = -\infty}^{\infty} \mathrm{a}[k] \, \,\mathrm{b}[n-k]$
Konstruktion:
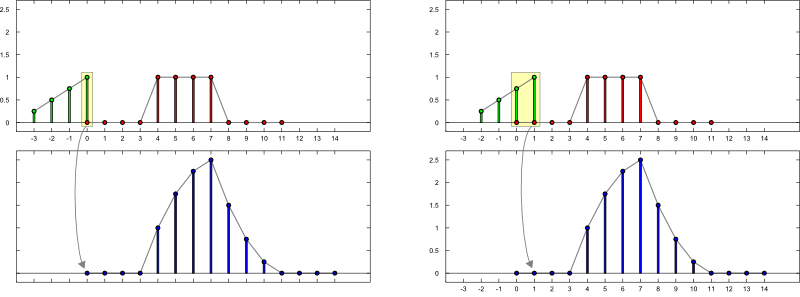
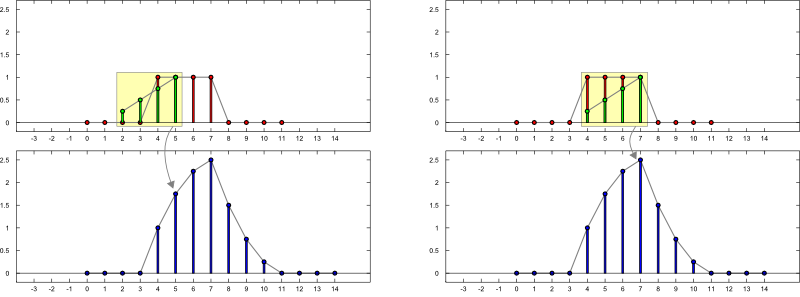
$\mathrm{f}[n] = \sum\limits_{k = -\infty}^{\infty} \mathrm{a}[k] \, \,\mathrm{b}[n-k]$
Konstruktion:


Anregungen oder Verbesserungsvorschläge können auch gerne per E-mail an mich gesendet werden: Kontakt