Zu jeder Schaltfunktion gibt es unendlich viele Boolesche Terme bzw. Ausdrücke und damit unendlich viele Schaltkreise, die sie realisieren. Boolesche Funktionen können wir in standardisierter Weise durch Boolesche Ausdrücke in so genannten Normalformen darstellen, diese führen oft zu komplexen Schaltkreisen. Um die komplexen Schaltkreisen zu minimieren bestimmt man das einfachste und billigste Boolesche Term bezüglich eines Kostenmaßes.
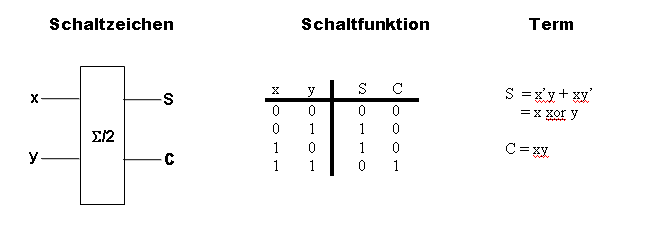
Der Halbaddierer hat die Aufgabe, zwei einstellige Dualzahlen zu addieren. Er besitzt zwei Eingänge (x und y) und zwei Ausgänge (S (für Summe) und C (Carry, Übertrag). An dem ersten Eingang liegt die erste Dualzahl x und an dem zweiten liegt die zweite Dualzahl y. An dem Ausgang S liegt die letzte Stelle der Summe (0 oder 1), an dem Ausgang C liegt der Übertrag (0 oder 1).

Aus den Booleschen Termen lässt sich die Realisierung des Halbaddierers gewinnen:
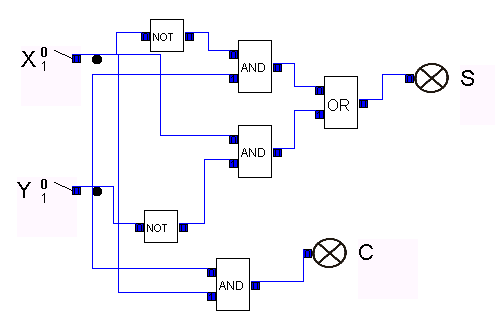
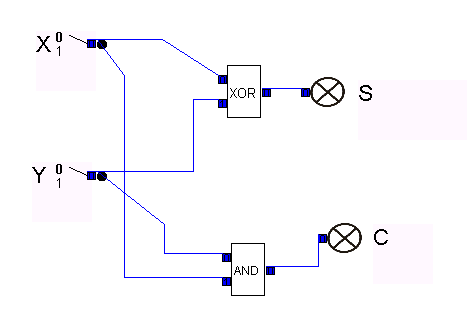
Will man zwei mehrstellige Dualzahlen addieren, reicht ein Halbaddierer nicht aus, weil ggf. der Übertrag der vorherigen Stelle mit berücksichtigt werden muss.
Man muss also eine Schaltung entwickeln, die insgesamt 3 einstellige Dualzahlen addieren kann.
Statt nun alle 8 möglichen Fälle zu untersuchen und für das Ergebnis geeignete Schaltungen zusammenzustellen, ist es einfacher,
Zu beachten ist dabei, dass bei jeder aber höchstens bei einer der Additionen ein Übertrag erfolgen kann.
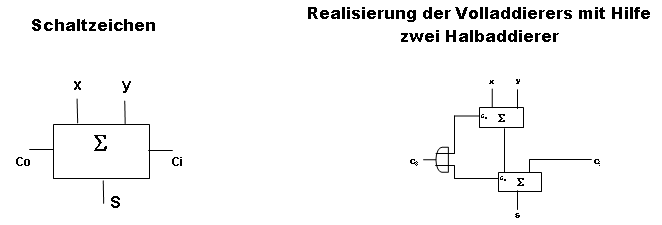
Also der Volladdierer hat die Aufgabe, drei einstellige Dualzahlen zu addieren. Er besitzt drei Eingänge (x, y und Ci (für carry in) und zwei Ausgänge (S (für Summe) und Co (für carry out). An den Eingängen liegen die drei Dualzahlen. An dem Ausgang S liegt die letzte Stelle der Summe (0 oder 1), an dem Ausgang C liegt der Übertrag (0 oder 1).
Ein Polynom ist eine Disjunktion von Monomen. Ein billiges Polynom zur Realisierung von f heißt Minimalpolynom von f.
Beispielpolynome:
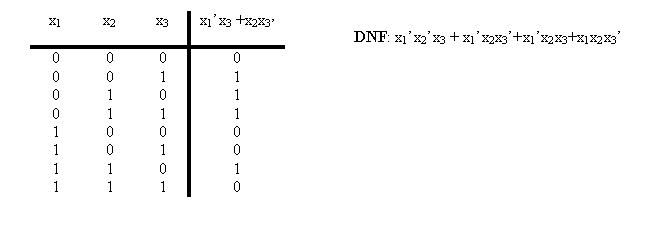
Vereinfachung der obigen DNF:
x1’x2’x3 + x1’x2x3’+x1’x2x3+x1x2x3’
= x1’(x2’ + x2)x3 + (x1’ + x1)x2x3’ Nach Komplementärregel gilt x2’+x2 = 1
= x1’1x3 + 1x2x3’ und es gilt 1*x = x
= x1’x3 + x2x3’
Diese Vereinfachung ist unter dem Namen Resolutionsregel bekannt, d.h:
Beispiel für mehrfache Anwendung der Resolutionsregel
Betrachte:
f(x1,x2,x3,x4)
= x1x2’x3x4 + x1x2’x3’x4 + x1x2x3x4 + x1’x2’x3’x4 + x1’x2’x3x4
= x1x2’x4 + x1x3x4 + x2’x3’x4 + x1’x2’x4
= x2x4 + x1x3x4 + x2’x3’x4
Die mehrfache Anwendung beruht dabei auf dem Gesetz x + x = x, die das Doppeln von Monome erlaubt: x1x2’x3x4 + x1x2’x3’x4 = x2’(x1x3x4 + x1x3’x4)
= x2’(x1x4(x3 + x3’))
= x2’(x1x4)1
= x2’x1x4
= x1x2’x4
Um die Übersicht über alle mögliche Resolutionen zu behalten, betrachtet man das graphische Verfahren, mit dem eine Schaltfunktion leicht vereinfachen werden kann:
Das Karnaugh-Diagramm einer Schaltfunktion mit drei oder vier Argumenten (in Bezeichnung f:2 hoch n -> 2 wobei n=3 oder n=4 ist eine graphische Darstellung von f durch:
* Eine m x n-Matrix ist eine Anordnung von mn Zahlen in einem rechteckigen Schema von m Zeilen und n Spalten.
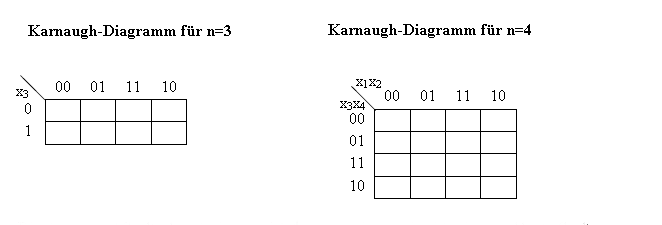
Die Zeilen- und Spaltenbeschriftung erfolgt so, dass sich zwei zyklisch benachbarte Spalten oder Zeilen nur in genau einer Komponente (Variablen bzw. Literale) unterschieden.
In die Felder der Matrix werden die Funktionswerte von f eingetragen, es reicht, die Wert 1 einzutragen.
Beispiel:
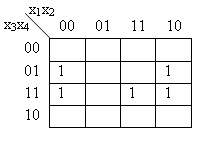
Man beachte dass je zwei benachbarte Einsen im Diagramm eine Resolution liefern und jedes Feld mit einer 1 entspricht einem Minterm der DFN.
Die vereinfachte Darstellung kriegt man in dem man alle im Karnaugh-Diagramm auftretenden Einsen durch möglichst große Blöcke der Form 2r x 2s und bildet die diesen Blöcken entsprechenden Monome.
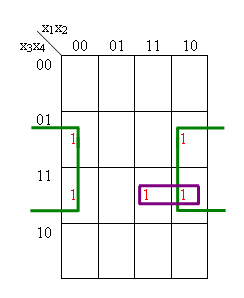
Zweierblock: x1x3x4
Viererblock: x2’x4
Also die vereinfachte Darstellung ist: f(x1,x2,x3,x4) = x1x3x4 + x2’x4
Bemerkung:
1. Beachte, dass auch im Falle der folgenden Karnaugh-Diagramms alle vier Ecken zu einem Vierblock zusammengefasst werden können:
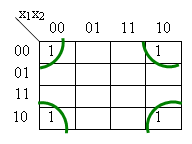
2. In seltenen Fällen ist es sinnvoll, nicht unbedingt von den größten Blöcke auszugehen. Auch die Minimierung der Anzahl der Blöcke ist relevant.

Ein Term bzw. eine Klausel C heißt Implikant einer Booleschen Funktion f, falls bei jeder Belegung der Variablen, die die Klausel C erfüllt, auch f den Wert 1 hat. Jede Klausel der DNF-Formel einer Booleschen Funktion f ist Implikant von f.
Ein Implikant M einer Booleschen Funktion f heißt Primimplikant von f, wenn er durch Resolution mit anderen Implikanten von f nicht weiter vereinfacht werden kann.
Im Karnaugh-Diagramm entsprechen rechteckige Blöcke von Einsen den Implikanten und maximale derartige Blöcke den Primimplikanten.
Bei Funktionen mit mehr als 6 Argumenten werden Karnaugh-Diagramme so unübersichtlich, dass das Verfahren kaum mehr anwendbar ist. Hier hilft das Tabellenverfahren nach Quine/McCluskey. Es geht davon aus, dass eine zu minimierende Funktion in DNF vorliegt; gegeben ist also die Menge der Minterme von f.
Das Verfahren sieht zwei Phasen vor:
In einem ersten Schritt werden alle Minterme nach steigender Anzahl der in ihnen vorkommenden negierten Variablen geordnet und in Gruppen gleicher Anzahl negierter Variablen gegliedert.
Im zweiten Schritt werden alle Resolutionsmöglichkeiten gesucht, die Resolutionen durchgeführt und die Ergebnisse in eine neue Tabelle aufgenommen. Resolutionsmöglichkeiten müssen nur zwischen Mitgliedern benachbarter Gruppen gesucht werden. In Iteration werden die beiden Schritte nun mit der neuen Tabelle durchgeführt. Es entsteht eine dritte Tabelle, die wiederum auf gleiche Art bearbeitet wird, und so weiter, bis das Verfahren mit einer Tabelle abbricht, in der keine Resolutionsmöglichkeiten mehr gegeben sind.
Diese Tabelle enthält dann genau alle Primimplikanten der bearbeiteten Funktion.
Beispiel:
Betrachte die folgende Funktion:
f(x1, x2 ,x3 , x4)
= x1x2x3x4´
+ x1x2x3´x4
+ x1x2x3´x4´
+ x1´x2´x3´x4´
+ x1´x2x3´x4´
+ x1´x2x3x4´
+ x1x2´x3x4
I.1) Die Funktion ist in DNF. Also teile seine Minterme anhand der Anzahl der vorkommenden Negationszeichen in Gruppen ein:
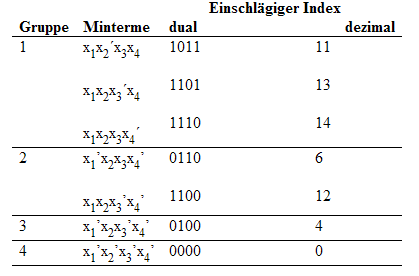
I.2) Betrachte alle Mintermpaare aus benachbarten Gruppen und versuche die Resolutionsregel anzuwenden. Bilde eine neue Tabelle, in der alle verkürzten Implikanten eingetragen werden. Ferner werden Monome, auf die die Resolutionsregel nicht mehr anwendbar ist, übernommen:
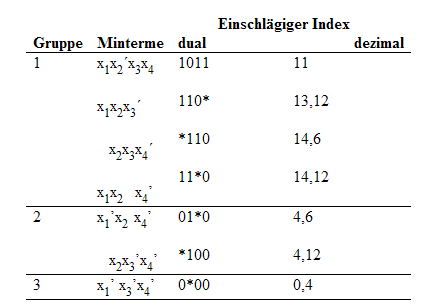
Das "*" beim dualen Index kennzeichnet dabei durch die Resolutionsregel herausgefallene Variablen.
I.3) Wiederhole Schritt I.2 bis sich keine Vereinfachung der Tabelle mehr ergibt d.h. bis sich die Tabelle nicht mehr ändert. Die Tabelle enthält dann genau die Primimplikanten

II.1) Kostenminimale Auswahl von Primimplikanten:
Man erstellt eine Matrix (aij) mit Primimplikanten als Zeilen und Mintermen der DNF als Spalten. Hierzu
dokumentiert die Matrix, welche Primimplikanten welche Minterme überdecken. Eine Eins wird in der
Tabelle eingetragen also aij = 1 falls der Minterm j von Primimplikant i überdeckt wird ansonsten 0.
Also mithilfe der letzten Tabelle kann man die Einsen in der Matrix eintragen, in dem man guckt welche
Minterme bei dem jeweiligen Primimplikant beteiligt und dann trägt man eine Eins ein.
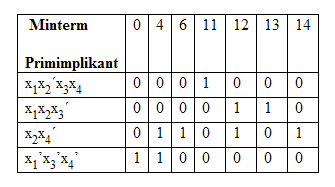
II.2) Anhand dieser Matrix wählt man in dieser Matrix eine Auswahl von Zeilen, d.h. Primimplikanten,
so dass:
i) die von diesen Zeilen gebildete Teilmatrix in jeder Spalte mindestens eine Eins enthält und
ii) die Gesamtkosten dieser Primimplikanten minimal sind unter allen möglichen Auswahlen mit (i)
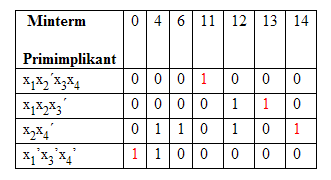
Der erste Primimlikant ist unbedingt notwendig, da Spalte 11 von keinem anderen überdeckt wird, ebenso der zweite, weil nur in dieser Zeile die Spalte 13 mit 1 belegt ist. Desgleichen sind der dritte 14 und der vierte Primplikant 0 wesentlich. In diesem Beispiel bleibt also für eine Auswahl kein Spielraum – alle Primimplikanten werden benötigt.
Die minimale disjunktive Form lautet daher: x1x2’x3x4 + x1x2x3’ + x2x4’ + x1’x3x4’.
Ein Schaltnetz implementiert eine Menge von Booleschen Funktionen mit technischen Mitteln, wobei die Implementierung vom Ideal abweichen kann. Wie bereits erwähnt, liegt eine wesentliche Abweichung in den Signallaufzeiten. Dies kann bei Eingangssignalwechsel zu sogenannten Hazards führen: Ausgänge nehmen für gewisse Übergangszeiten Werte an, die nicht den vorgegebenen Booleschen Funktionen entsprechen. Ist die Schaltung in eine Umgebung eingebettet, die dies nicht toleriert, kann es zu einem Fehlverhalten der Gesamtschaltung führen.
Also Hazard ist eine Fehlermöglichkeit einer Schaltung aufgrund von Laufzeitfehlern.
Man unterscheidet Funktions- und Schaltungshazards.
Funktionshazards treten schon bei Booleschen Funktionen auf. Wenn beim Übergang von einer Eingangskombination zu einer anderen die Eingangssignale ihre Werte zu unterschiedlichen Zeitpunkten ändern (etwa durch unterschiedliche Verzögerungen im Vorfeld der Eingänge bedingt), dann können zwischenzeitlich Ausgangswerte auftreten, die weder der alten noch der neuen Eingangskombination entsprechen..
Schaltungshazards sind durch das Schaltnetz selbst und dort vorhandene unterschiedliche Laufzeiten der einzelnen Signalwege bedingt. Man schränkt Schaltungshazards auf die Fälle ein, bei denen keine Funktionshazards vorliegen.
Beispiel: Schaltungshazard
Gegeben sei folgendes Schaltnetz für f(x1,x2,x3)= x1x3 + x2x3’
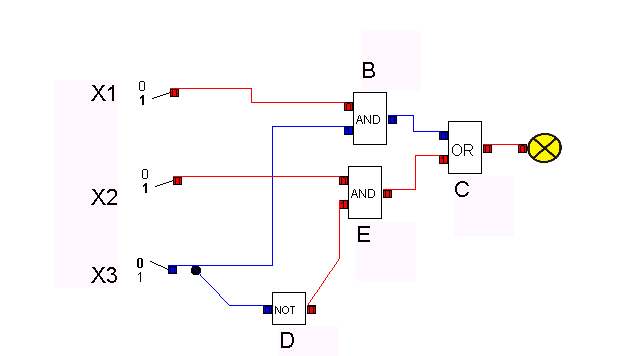
f(1,1,0) = f(1,1,1) = 1, aber Ausgang kurzzeitig auf 0, falls Signalweg x3-B-C langsamer als D-E-C.
Schaltungshazards können durch zusätzlichen Schaltungsaufwand vermieden werden.
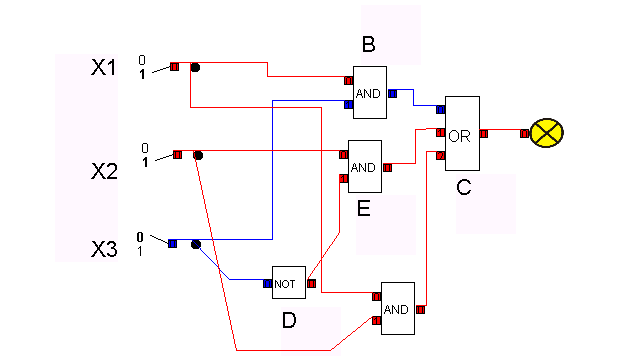
Man entwerfe für verschiedene Schaltfunktionen einen universellen verwendbaren Einheitsbaustein mit möglichst homogener Netzstruktur, der für unterschiedliche Anwendungen eingesetzt werden kann. Naturgemäß wird ein solche Baustein etwas aufwendiger sein als eine Schaltung, welche nur im Hinblick auf eine Anwendung entworfen wird, dafür darf man andererseits einen übersichtlichen Aufbau sowie eine hohe Wartungsfreundlichkeit erwarten, was insbesondere für die Herstellung, das Testen und den Betrieb eines solchen Bausteins von großer Bedeutung ist.
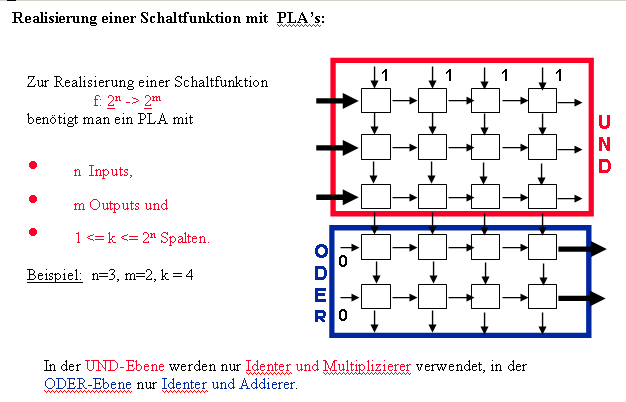
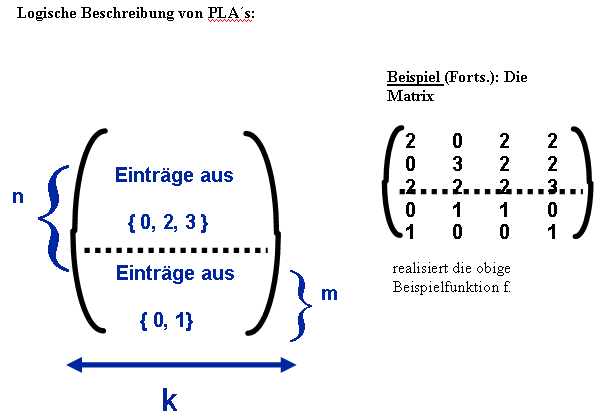
Das heute tatsächlich verwendete Typ eines derartigen Einheitsbausteins ist das Programmierbare Logische Feld (PLA), welches die folgende Struktur hat:
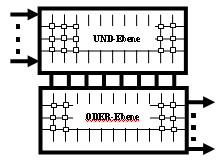
Intern ist ein PLA gitterförmig verdrahtet, wobei sich an jedem Kreuzpunkt von zwei Drähten ein einheitlich formatierter Baustein befindet. Ein solches "Kästchen" ist in der obige Darstellung eingezeichnet und in einer Ausschnittsvergrößerung sieht dieses so aus:
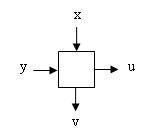
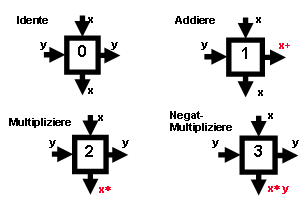
Die Gitterbausteine sind mit 0,1,2,3 bezeichnet. Mindestens einer der beiden Eingaben (bzw. Inputs) wird an einen Ausgang unverändert weitergegeben, bei Ideneter sogar beide. Der Addierer liefert am "rechten" Ausgang die Summe (im Sinne von "ODER") seiner Inputs, die Multiplizierer am "unteren" Ausgang x*y bzw xy’. Angemerkt sei, dass diese Bausteine auch leicht durch Gatter beschreibbar sind.
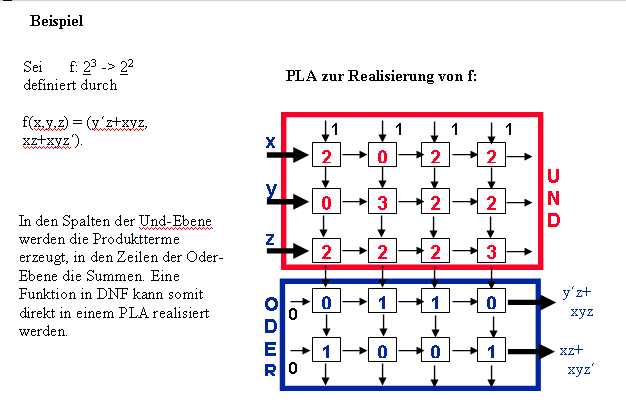
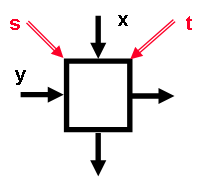 |
Die Steuereingänge s und t bestimmen das Verhalten des Bausteins:
|