Grafikprogrammierung
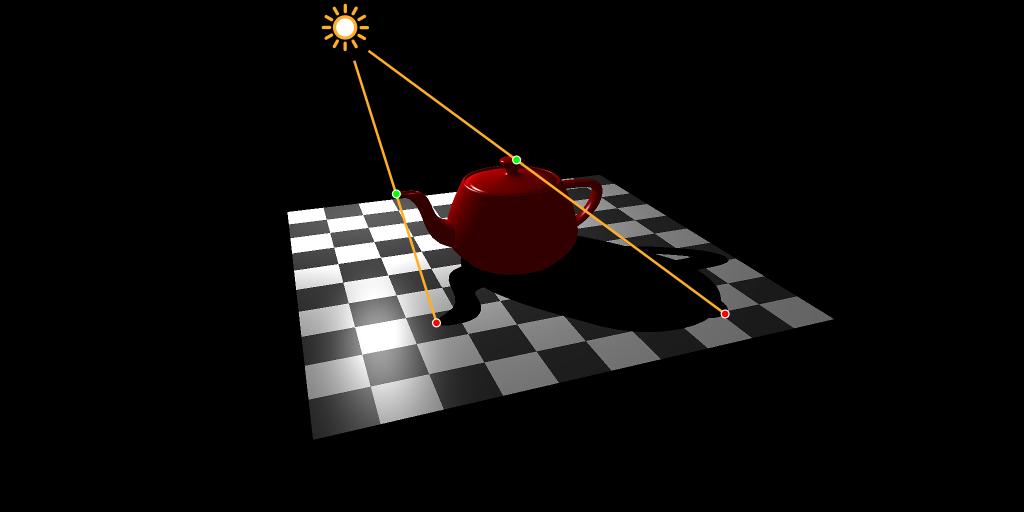
Schatten

• Schatten sind für den Realismus der Szene und zum Einschätzen von Objektabständen sehr wichtig
• Unser bisheriges Beleuchtungsmodell berücksichtigt jedoch keine Schatten
• Alle Lichtquellen in Richtung der Oberflächennormale (Halbraum) wurden bisher als sichtbar angenommen
• Dies hatte den Vorteil, dass die Beleuchtungsberechnung nur abhängig vom aktuellen Polygon (bzw. Fragment) ist
• Bei einer Schattenberechnung müssen jedoch alle anderen Polygone bekannt sein, da jedes andere Polygon die Lichtquelle für das aktuelle Fragment verdecken kann
• Der Sichtbarkeitstest für eine Lichtquelle ist somit aufwendig und wird nicht direkt von OpenGL-Pipeline unterstützt
• Dieses Kapitel stellt einige Verfahren vor, die eine Schattenberechnung in Echtzeit ermöglichen

Projektion auf Ebene $z=0$

• Idee: Projektion des Objekts auf eine planare Ebene
• Z.B. einfache Parallelprojektion auf die Ebene $z=0$ mit folgender Matrix:
  $\mathtt{T}_{\tiny \mbox{shadow}} = \begin{bmatrix}1 & 0& 0 & 0\\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 &1\end{bmatrix}$
• Diese Transformation muss im Weltkoordinantensystem angewendet werden, d.h.
  $\underline{\tilde{\mathbf{P}}} = \mathtt{A} \, \underbrace{\mathtt{T}_{\mathrm{\small cam}}^{-1} \, \mathtt{T}_{\tiny \mbox{shadow}} \, \mathtt{T}_{\mathrm{\small obj}}}_{\mathtt{T}_{\mathrm{\small modelview}}} \, \underline{\mathbf{P}}$
• Projiziertes Objekt zusätzlich zur ursprünglichen Szene mit schwarzer Farbe malen

• Projektion des verdeckenden Objekts auf eine planare Fläche bei gegebener Position einer Punktlichtquelle
• Projiziertes Objekt zusätzlich zur ursprünglichen Szene mit schwarzer Farbe malen

$x$

$z$

Stützpunkt $\mathbf{P}=(p_x, p_y, p_z)^\top$

projizierter Stützpunkt $\tilde{\mathbf{P}}=(\tilde{p}_x, \tilde{p}_y, \tilde{p}_z)^\top$

Lichtquelle $\mathbf{L}=(l_x, l_y, l_z)^\top$

• Bei gegebener Position der Lichtquelle $\mathbf{L}=(l_x, l_y, l_z)^\top$ berechnet sich der auf die Ebene $z=0$ projizierter Stützpunkt $\tilde{\mathbf{P}}=(\tilde{p}_x, \tilde{p}_y, \tilde{p}_z)^\top$ aus dem originalen Stützpunkt $\mathbf{P}=(p_x, p_y, p_z)^\top$ mit Hilfe des Strahlensatzes (siehe Abbildung) zu:
  $\frac{\tilde{p}_x - l_x}{l_z} = \frac{p_x - l_x}{l_z - p_z} \Leftrightarrow \tilde{p}_x = \frac{p_x - l_x}{l_z - p_z} l_z+ l_x = \frac{p_x l_z - l_x l_z + l_x l_z - l_x p_z}{l_z - p_z} = \frac{l_z p_x - l_x p_z}{l_z - p_z}$

• Damit gilt:
  $\tilde{p}_x = \frac{l_z p_x - l_x p_z}{l_z - p_z} \quad \quad\tilde{p}_y = \frac{l_z p_y - l_y p_z}{l_z - p_z} \quad \quad\tilde{p}_z = 0$
• Bei Verwendung von homogene Koordinaten kann diese Abbildungsvorschrift ebenfalls als projektive $4 \times 4$ Matrix geschrieben werden:
  $ \tilde{\underline{\mathbf{P}}} = \begin{pmatrix}\tilde{x}\\ \tilde{y} \\ \tilde{z} \\ \tilde{w} \end{pmatrix}= \underbrace{\begin{bmatrix}l_z & 0& -l_x & 0\\ 0 & l_z & -l_y & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & -1 & l_z\end{bmatrix}}_{\mathtt{T}_{\tiny \mbox{shadow}} } \begin{pmatrix}p_x\\p_y\\p_z\\1\end{pmatrix}$

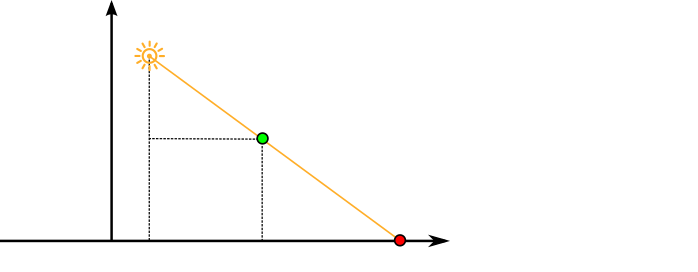
  $\tilde{\underline{\mathbf{P}}} = \begin{pmatrix}\tilde{x}\\ \tilde{y} \\ \tilde{z} \\ \tilde{w} \end{pmatrix} \in \mathbb{H}^3 \quad \longmapsto \quad \tilde{\mathbf{P}} = \begin{pmatrix} \tilde{p}_x\\ \tilde{p}_y\\ \tilde{p}_z \end{pmatrix} = \begin{pmatrix}\frac{\tilde{x}}{\tilde{w}}\\\frac{\tilde{y}}{\tilde{w}}\\\frac{\tilde{z}}{\tilde{w}} \end{pmatrix} \in \mathbb{R}^3 $

• Bei Anwendung im globalen Koordinatensystem ergibt sich wieder insgesamt:
  $\underline{\tilde{\mathbf{P}}} = \mathtt{A} \, \mathtt{T}_{\mathrm{\small cam}}^{-1} \, \mathtt{T}_{\tiny \mbox{shadow}} \, \mathtt{T}_{\mathrm{\small obj}}\, \underline{\mathbf{P}}$

• Projektion auf $z=0$:
  $ \mathtt{T}_{\tiny \mbox{shadow}} = \begin{bmatrix}l_z & 0& -l_x & 0\\ 0 & l_z & -l_y & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & -1 & l_z\end{bmatrix}$
• Projektion auf $y=0$:
  $ \mathtt{T}_{\tiny \mbox{shadow}} = \begin{bmatrix}l_y & -l_x &0& 0\\ 0 & 0 & 0 & 0 \\ 0 & -l_z & l_y & 0 \\ 0 & -1 & 0 & l_y\end{bmatrix}$
• Projektion auf $x=0$:
  $ \mathtt{T}_{\tiny \mbox{shadow}} = \begin{bmatrix}0 & 0 &0& 0\\ -l_y & l_x & 0 & 0 \\ -l_z & 0 & l_x & 0 \\ -1 & 0 & 0 & l_x\end{bmatrix}$

• GSN Composer: PlanarShadow

• Eigentlich sollte der ambiente Anteil des Beleuchtungsmodells im Schatten sichtbar bleiben
• Dazu muss die Szene jedoch zweifach gerendert werden
  • 1. Durchgang: Diffuser und spekularer Anteil inklusive Schatten
  • 2. Durchgang: Nur ambienter Anteil ohne Schatten

Diffuser und spekularer Anteil

Ambienter Anteil

Ergebnis

+

=

• In diesem Schritt muss die die Szene aus Sicht der Lichtquelle gerendert werden
• Dies ist relativ einfach für einen Strahler (engl. "Spotlight"), da dieser eine 3D-Position $\mathbf{p}$, eine Hauptausstrahlrichtung $\mathbf{d}$ und einen äußerer Öffnungswinkel $\beta_{\tiny \mbox{outer}}$ besitzt
• Für die Positionierung der "Licht"-Kamera mittels $\mathtt{T}_{\mathrm{\tiny cam/light}}^{-1}$ kann beispielsweise die Funktion gluLookAt verwendet werden (siehe Teil 6, Kapitel 1)

  gluLookAt(eyex, eyey, eyez, refx, refy, refz, upx, upy, upz);

  • Der Augpunkt $\mathbf{c}_{\mathrm{\small eye}}$ der Kamera enspricht der 3D-Position $\mathbf{p}$ des Stahlers
  • Der anvisierten Referenzpunkts $\mathbf{p}_{\mathrm{\small ref}}$ ergibt sich durch:
    $\mathbf{p}_{\mathrm{\small ref}} = \mathbf{p} + \mathbf{d}$
• Die Projektionsmatrix $\mathtt{A}_{\mathrm{\tiny cam/light}}$ kann mit der Funktion gluPerspective generiert werden (siehe Teil 6, Kapitel 1)

  gluPerspective(fovy, aspect, near, far)

  • Dabei ist der Öffnungswinkel der Kamera fovy $=\beta_{\tiny \mbox{outer}}$

Lichtposition

Shadow Map

0.0

1.0

0.0

1.0

• Zur Projektion der Shadowmap müssen die zugehörigen Texturkoordinaten für jedes Vertex ermittelt werden
• Nach Anwenden von
  $\underline{\tilde{\mathbf{P}}} = \mathtt{A}_{\mathrm{\tiny cam/light}} \, \mathtt{T}_{\mathrm{\tiny cam/light}}^{-1} \, \mathtt{T}_{\mathrm{\small obj}}\, \underline{\mathbf{P}}$
  und perspektivischer Division liegen die $x$-, $y$-, und $z$-Koordinate eines Vertex im Bereich [-1.0, 1.0]
• Als Texturkoordinaten werden jedoch $s$- und $t$-Koordinaten im Bereich [0.0, 1.0] benötigt. Dies kann durch eine zusätzliche Transformation erreicht werden:
  $\begin{pmatrix}\tilde{s}\\\tilde{t}\\\tilde{p}\\\tilde{q}\end{pmatrix} = \underbrace{\begin{bmatrix}0.5 & 0 & 0 & 0.5\\0 & 0.5 & 0 & 0.5\\0 & 0 & 0.5 & 0.5\\0 & 0 & 0 & 1.0\end{bmatrix} \, \mathtt{A}_{\mathrm{\tiny cam/light}} \, \mathtt{T}_{\mathrm{\tiny cam/light}}^{-1}}_{\mathtt{T}_{\tiny \mbox{shadow}}} \,\,\mathtt{T}_{\mathrm{\small obj}}\, \underline{\mathbf{P}}$

• Nach perspektivischer Division ergibt sich:
  $\begin{pmatrix}\tilde{s}\\\tilde{t}\\\tilde{p}\\\tilde{q}\end{pmatrix} = \underbrace{\begin{bmatrix}0.5 & 0 & 0 & 0.5\\0 & 0.5 & 0 & 0.5\\0 & 0 & 0.5 & 0.5\\0 & 0 & 0 & 1.0\end{bmatrix} \, \mathtt{A}_{\mathrm{\tiny cam/light}} \, \mathtt{T}_{\mathrm{\tiny cam/light}}^{-1}}_{\mathtt{T}_{\tiny \mbox{shadow}}} \,\,\mathtt{T}_{\mathrm{\small obj}}\, \underline{\mathbf{P}}$
  $\begin{pmatrix}s\\t\\p\end{pmatrix} = \begin{pmatrix}\frac{\tilde{s}}{\tilde{q}}\\ \frac{\tilde{t}}{\tilde{q}} \\ \frac{\tilde{p}}{\tilde{q}} \end{pmatrix} \in \mathbb{R}^3 $
• Dabei sind $s$ und $t$ die gesuchten Texturkoordinaten und $p$ der wahre Abstand zwischen Vertex und Lichtposition in Tiefenbuffer-Skalierung (alle drei Werte liegen im Bereich [0.0, 1.0] )
• Die Tiefenbuffer-Skalierung ist dabei abhängig von der gewählten Near- und Far-Ebene bei der Erstellung von $\mathtt{A}_{\mathrm{\tiny cam/light}}$

• Der wahre Abstand eines Fragments zu Lichtquelle ist gegeben durch:
  $z_{\mathrm{\small true}} = p$
• Der Abstand zum nächsten Objekt aus Sicht der Lichtquelle ist gegeben durch Nachschlagen in der der Shadow Map:
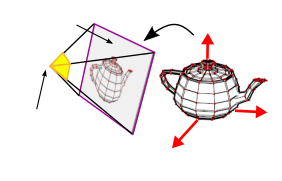
  $z_{\mathrm{\small nearest}} =$ texture(shadowmap, vec2(s,t));
• Ist $z_{\mathrm{\small nearest}} < z_{\mathrm{\small true}}$ ist das Fragment durch ein anderes Polygon verdeckt und somit im Schatten

Punkt im Schatten

Punkt im Licht

Lichtposition

Shadow Map

Framebuffer

Kamera

$z_{\mathrm{\small nearest}}$

$z_{\mathrm{\small true}}$

$z_{\mathrm{\small nearest}}$

$z_{\mathrm{\small true}}$

• GSN Composer: ShadowMap

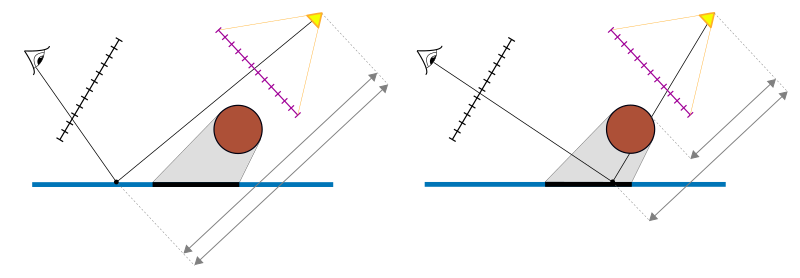
Vertex Shader :

#version 300 es
precision highp float; 
precision highp int; 

in vec3 position; // input vertex position from mesh
in vec2 texcoord; // input vertex texture coordinate from mesh
in vec3 normal;   // input vertex normal from mesh

uniform mat4 cameraLookAt; // camera look at matrix
uniform mat4 cameraProjection; // camera projection matrix
uniform mat4 spotLightTransform; // transformation matrix for the spot light
uniform mat4 meshTransform; // mesh transformation
uniform mat4 meshTransformTransposedInverse; // transposed inverse meshTransform
uniform mat4 shadowTransform; // shadow map transformation

out vec2 tc; // output texture coordinate of vertex
out vec3 wfn; // output fragment normal of vertex in world coordinate system
out vec3 vertPos; // output 3D position in world coordinate system
out vec4 shadowCoord; // output texture coordinate in shadow map

void main(){
  tc = texcoord;
  wfn = vec3(meshTransformTransposedInverse * vec4(normal, 0.0));
  vec4 vertPos4 = meshTransform * vec4(position, 1.0);
  vertPos = vec3(vertPos4) / vertPos4.w;
  
  //texture coordinates in shadow map
  shadowCoord = shadowTransform * vertPos4;
  
  gl_Position = cameraProjection * cameraLookAt * vertPos4;
}

Fragment Shader :

#version 300 es
precision highp float;
precision highp int;
out vec4 outColor;

in vec2 tc; // texture coordinate of pixel (interpolated)
in vec3 wfn; // fragment normal of pixel (interpolated)
in vec3 vertPos; // fragment vertex position (interpolated)
in vec4 shadowCoord; // texture coordinate in shadow map  (interpolated)

uniform int mode; // debug mode
uniform sampler2D diffuseTex; // diffuse texture
uniform float ambientFactor; // ambient factor
uniform vec4 specularColor; // specular color
uniform float shininess; // specular shininess exponent
uniform vec4 lightColor; // color of light
uniform vec3 lightPosition; // light position in world space
uniform vec3 lightDirection; // spot light direction in world space
uniform float lightCutoff; // spot light cut off
uniform float lightExponent; // spot light exponent
uniform float lightAttenuation; // quadratic light attenu.
uniform vec3 cameraPos; // camera position in world space
uniform float shadowBias; // shadow bias
uniform sampler2D shadowMap; // shadow map


vec3 blinnPhongBRDF(vec3 lightDir, vec3 viewDir, vec3 normal, 
            vec3 phongDiffuseCol, vec3 phongSpecularCol, float phongShininess) {
  vec3 color = phongDiffuseCol;
  vec3 halfDir = normalize(viewDir + lightDir);
  float specDot = max(dot(halfDir, normal), 0.0);
  color += pow(specDot, phongShininess) * phongSpecularCol;
  return color;
}

vec3 blinnPhongShading(vec3 n, vec3 viewDir, vec3 lightDir, vec4 lightColor, 
                       float lightAttenuation, vec4 diffuseColor, vec4 specColor, 
                       float shininess, float ambientFactor) 
{
  // ambient Term
  vec3 radiance = ambientFactor * diffuseColor.rgb;
  // irradiance contribution from light
  float irradiance = max(dot(lightDir, n), 0.0); 
  if(irradiance > 0.0) { // if receives light
    vec3 brdf = blinnPhongBRDF(lightDir, viewDir, n, 
                                diffuseColor.rgb, specColor.rgb, shininess);
    radiance += brdf * irradiance * lightColor.rgb * lightAttenuation;
  }
  return radiance;
}

void main() {
  vec3 lightVec = lightPosition - vertPos;
  float d = length(lightVec); // distance to light
  vec3 lightDir = normalize(lightVec);
  vec3 normal = normalize(wfn.xyz);
  vec3 viewDir = normalize(cameraPos - vertPos);

  // compute shadow;
  vec4 shadowCoordDiv = shadowCoord / shadowCoord.w;
  float nearestZ = texture(shadowMap, shadowCoordDiv.st).z;
  float trueZ = shadowCoordDiv.z - shadowBias;
  float shadowVal = nearestZ < trueZ ? 0.5 : 1.0;

  float shadow = shadowVal;
  if(dot(lightDir, normal) <= 0.0) {
    shadow = 0.5;
  }

  // attenuation due to spot
  float attenuation = abs(dot(lightDir, lightDirection));
  if(attenuation < lightCutoff) {
    attenuation = 0.0;
  } else {
    attenuation = pow(attenuation, lightExponent);
    // atttenuation due to quadratic distance fall off
    attenuation *= 1.0 / (lightAttenuation * d * d);
  }

  vec4 diffuseColor = texture(diffuseTex, tc);
  vec4 color = ambientFactor * diffuseColor * lightColor;
  color.a = 1.0;

  if(shadow > 0.75) {
    color.rgb = blinnPhongShading(normal, viewDir, lightDir, 
                  lightColor, attenuation, diffuseColor, specularColor, 
                  shininess, ambientFactor);
  }

  outColor = clamp(color, 0.0, 1.0);
}

• Aufgrund der endlichen Auflösung der Shadow Map und der Quantisierung (Rundung) der enthaltenden Tiefenwerte kommt es beim Vergleich der Tiefen $z_{\mathrm{\small nearest}}$ und $z_{\mathrm{\small true}}$ zu Ungenauigkeiten
• Dies wird versucht durch einen "Shadow Bias" (auch genannt "Polygon Offset", "Depth Bias") zu kompensieren
  

  ohne Offset passender Offsetzu großer Offset
• Ein zu kleiner Offset kann "Shadow Leaking" verursachen, bei zu großem Offset erscheint der Schatten an der falschen Stelle und Objekte beginnen "zu fliegen"

• Vorteile
  • Beliebige Empfängerflächen
  • Selbstverschattung
  • Relativ schnelle Berechnung
• Nachteile
  • Treppenstufen-Effekte an Schattenkanten (Aliasing)
  • Shadow Bias ist abhängig von der Szene
  • Zunächst nur für Strahler
• Erweiterungen:
  • Richtungslichtquelle ⟶ Cascaded Shadow Maps (CSM)
  • Punktlichtquelle ⟶ Omnidirectional Shadow Mapping