Steuerungstasten

→ nächste Folie (auch Enter oder Spacebar).
← vorherige Folie
 d  schaltet das Zeichnen auf Folien ein/aus
 p  wechselt zwischen Druck- und Präsentationsansicht
CTRL  +  vergrößert die Folien
CTRL  -  verkleinert die Folien
CTRL  0  setzt die Größenänderung zurück

Das Weiterschalten der Folien kann ebenfalls durch das Klicken auf den rechten bzw. linken Folienrand erfolgen.

Notation

Typ Schriftart Beispiele
Variablen (Skalare) kursiv $a, b, x, y$
Funktionen aufrecht $\mathrm{f}, \mathrm{g}(x), \mathrm{max}(x)$
Vektoren fett, Elemente zeilenweise $\mathbf{a}, \mathbf{b}= \begin{pmatrix}x\\y\end{pmatrix} = (x, y)^\top,$ $\mathbf{B}=(x, y, z)^\top$
Matrizen Schreibmaschine $\mathtt{A}, \mathtt{B}= \begin{bmatrix}a & b\\c & d\end{bmatrix}$
Mengen kalligrafisch $\mathcal{A}, B=\{a, b\}, b \in \mathcal{B}$
Zahlenbereiche, Koordinatenräume doppelt gestrichen $\mathbb{N}, \mathbb{Z}, \mathbb{R}^2, \mathbb{R}^3$

Prozedurale Texturen

Prozedurale Texturen

  • Prozedurale Texturen erzeugen Muster bzw. Strukturen, die im Shader aus den Textur-Koordinaten berechnet werden
  • Die Muster werden also nicht aus einer Bitmap-Textur gelesen, sondern aus mathematischen Formeln berechnet
  • Dadurch sind prozedurale Texturen nicht von der Auflösung einer Bitmap-Textur abhängig und können beliebig nah betrachtet werden, ohne zu verpixeln (vergleichbar mit einer Vektorgrafik)

Signed Distance Function (SDF) eines Kreises

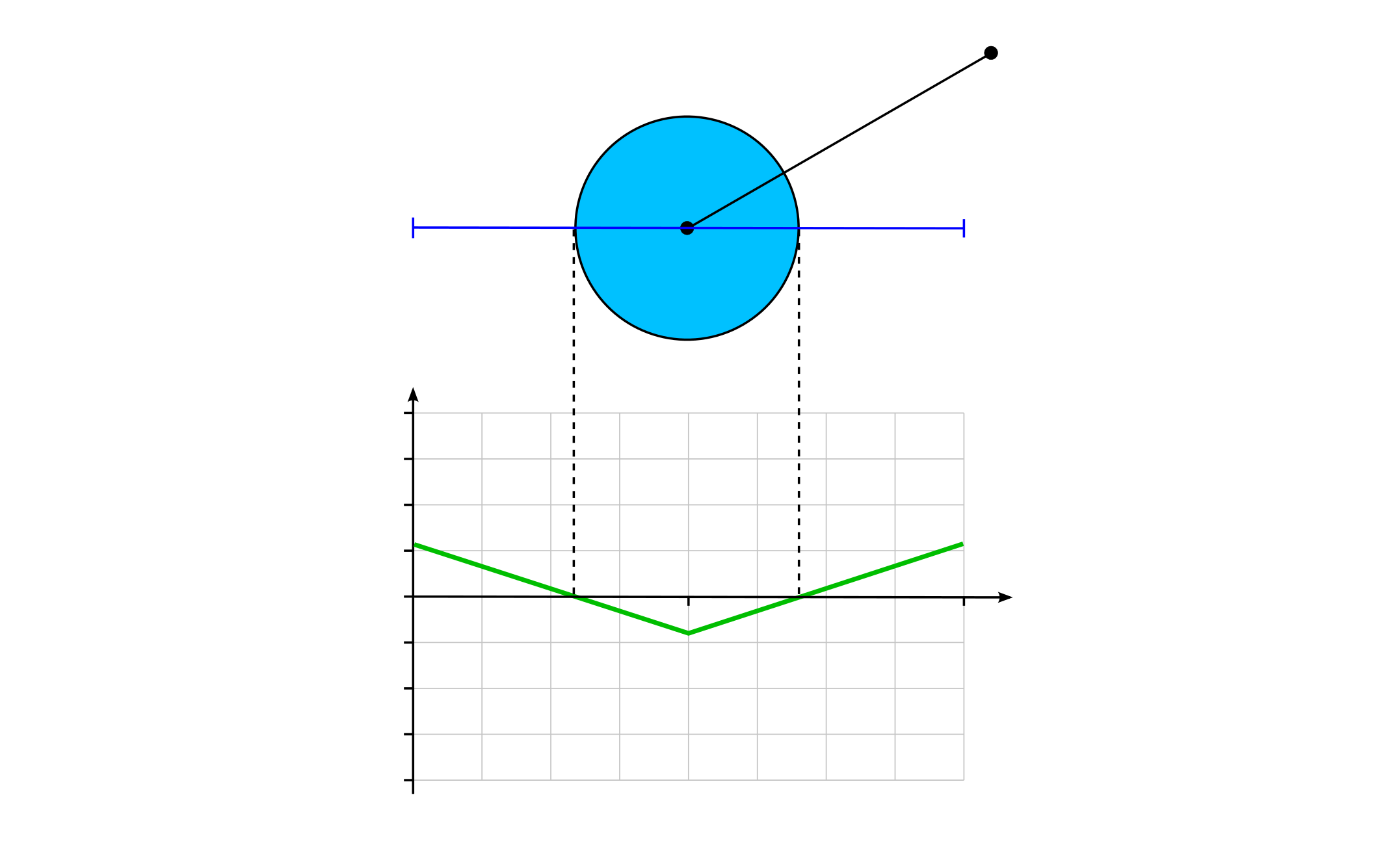
circle_sdf_05
$r$
$\mathbf{c}$
$\mathbf{p}$
$\operatorname{sdf} = |\mathbf{p} - \mathbf{c}| - r$
$1.0$
$1.0$
$1.0$
$-1.0$
$0.5$
$-0.5$
$0.0$
$0.0$
$\operatorname{sdf}$

Fill- und Stroke-Funktionen für SDFs

  • Fill 
    float fill(float sdf) {
    return step(0.0, -sdf);
  }
  • Stroke 
    float stroke(float sdf, float strokeWidth) {
  return fill(abs(sdf) - strokeWidth);
}

Mengenoperationen für SDFs

twocircles
  • Vereinigungsmenge 
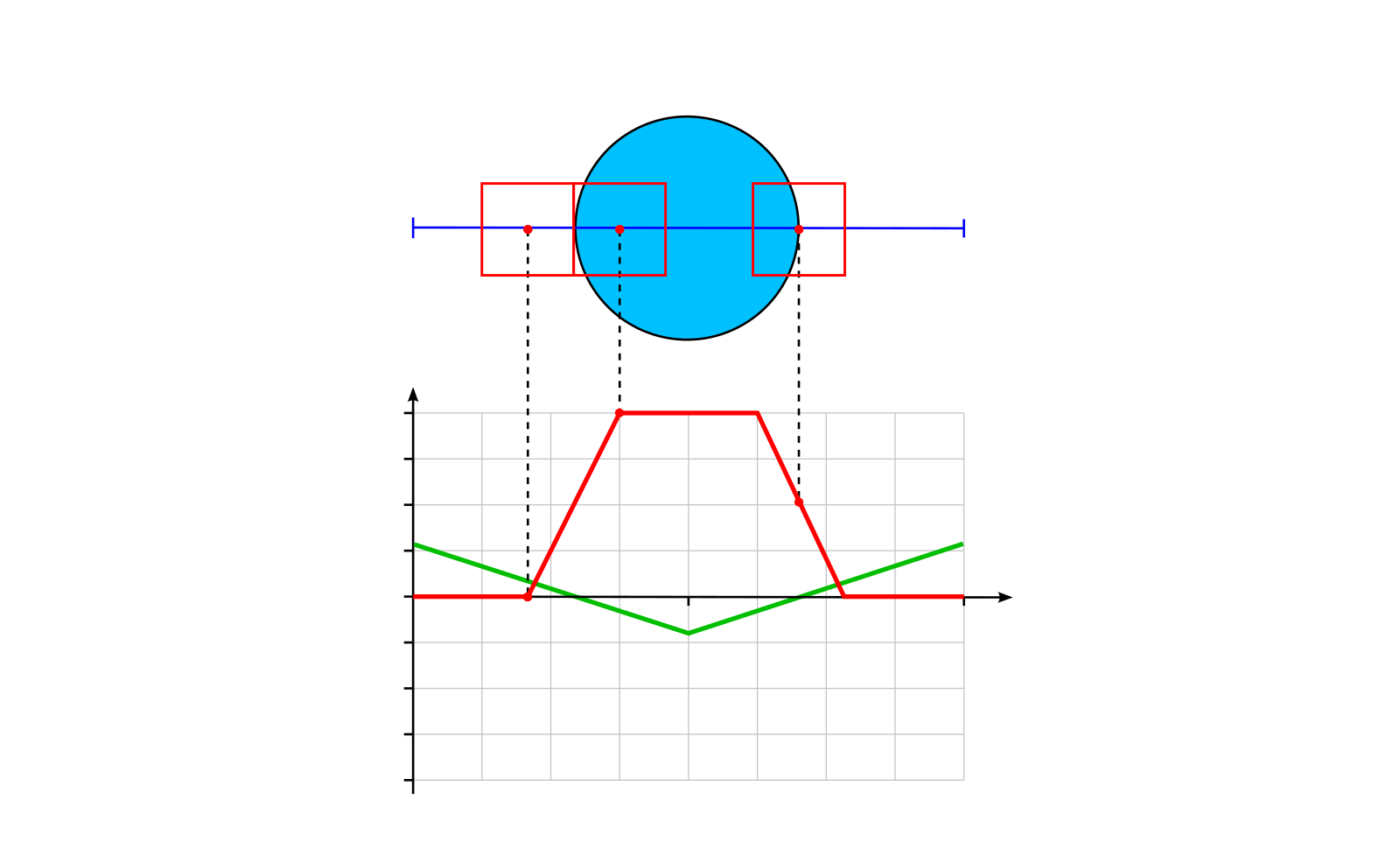
    float unionSDF(float sdf0, float sdf1) { 
  return min(sdf0, sdf1); 
}
  • Differenzmenge 
    float differenceSDF(float sdf0, float sdf1) { 
  return max(sdf0, -sdf1); 
}
  • Schnittmenge 
    float intersectionSDF(float sdf0, float sdf1) { 
  return max(sdf0, sdf1); 
}

Anti-Aliasing für Fill

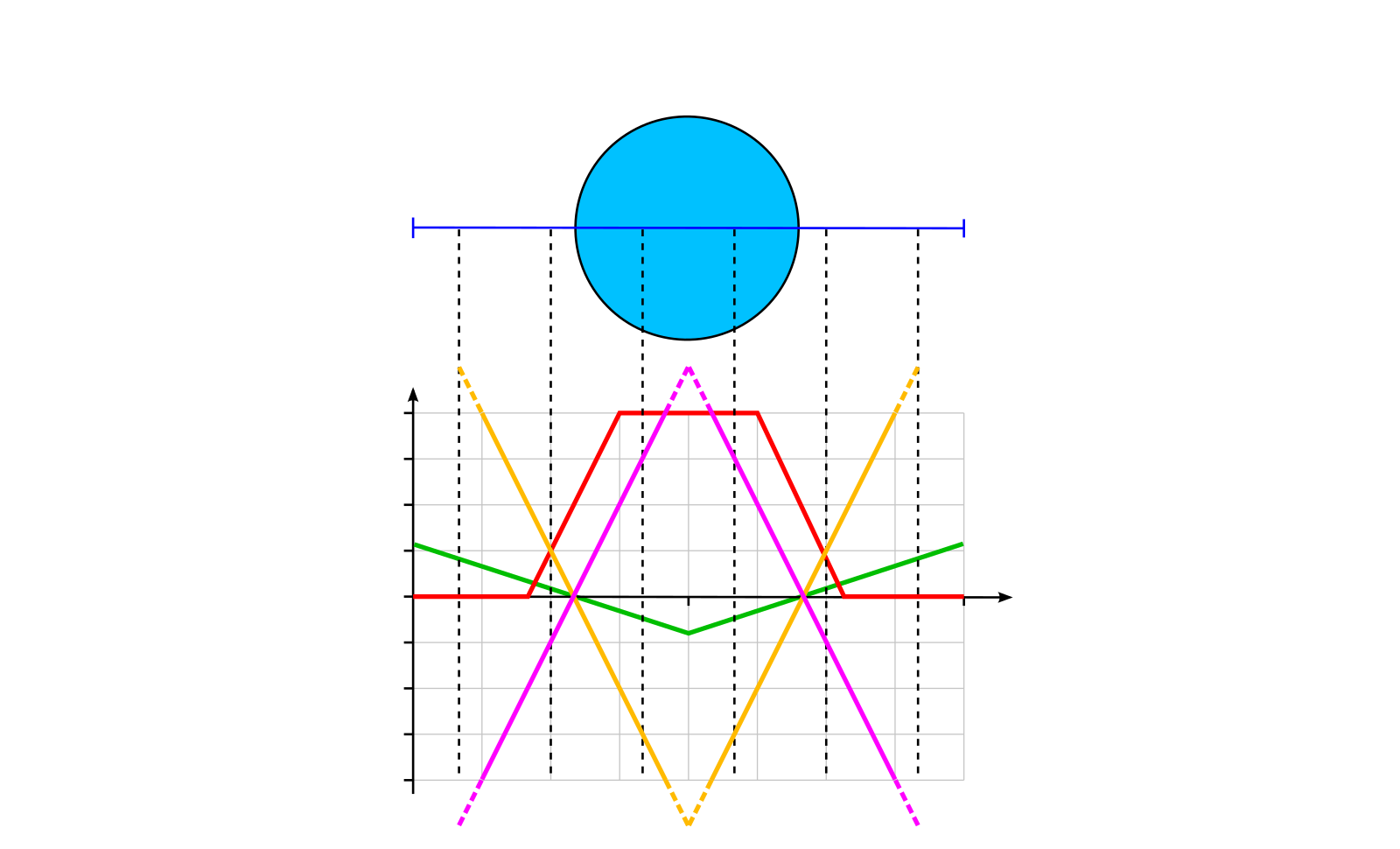
circle_sdf_anti-aliasing
$1.0$
$1.0$
$-1.0$
$0.5$
$-0.5$
$0.0$
$\operatorname{sdf}$
gesuchte Fill-Funktion

Anti-Aliasing für Fill

circle_sdf_anti-aliasing
$1.0$
$1.0$
$-1.0$
$0.5$
$-0.5$
$0.0$
$\operatorname{sdf}$
$\operatorname{clamp}\left(0.5 - \frac{\operatorname{sdf}}{\operatorname{fwidth}(\operatorname{sdf})}, 0.0, 1.0\right)$
$\frac{\operatorname{sdf}}{\operatorname{fwidth}(\operatorname{sdf})}$
$-\frac{\operatorname{sdf}}{\operatorname{fwidth}(\operatorname{sdf})}$

Anti-Aliasing-Funktionen für Fill und Stroke

  • Anti-aliased Fill Function 
    float fill(float sdf) {
  return clamp(0.5 - sdf / fwidth(sdf), 0.0, 1.0);
}
  • Stroke 
    float stroke(float sdf, float strokeWidth) {
  return fill(abs(sdf) - strokeWidth);
}

Beispiel: Prozedurale Texturen

teapot_dots
  • GSN Composer: Dots

Prozedurales Rauschen

Prozedurales Rauschen

  • Prozedurales Rauschen wird in der Computergrafik als Grundlage für diverse Rendering-Effekte benötigt
  • Beispiele sind: Wolken, Rauch, Wellen, Holzmaserungen, Verunreinigungen, prozedurale Landschaften usw.

Erzeugung von Pseudo-Zufallszahlen

  • Generieren von Zahlen, die scheinbar statistisch durch einen echten Zufallsprozess generiert wurden, tatsächlich jedoch durch eine deterministische Funktion erzeugt wurden
  • Die Ausgabe einer deterministischen Funktion ist reproduzierbar, d.h. sie generiert für dieselben Eingabeparameter dieselben Zahlen
  • In der Veröffentlichung "Hash Functions for GPU Rendering", (2020) von Mark Jarzynski und Marc Olano wird der PCG-Hash (Permuted Congruential Generator) empfohlen (gute Qualität bei geringer Rechenzeit): 
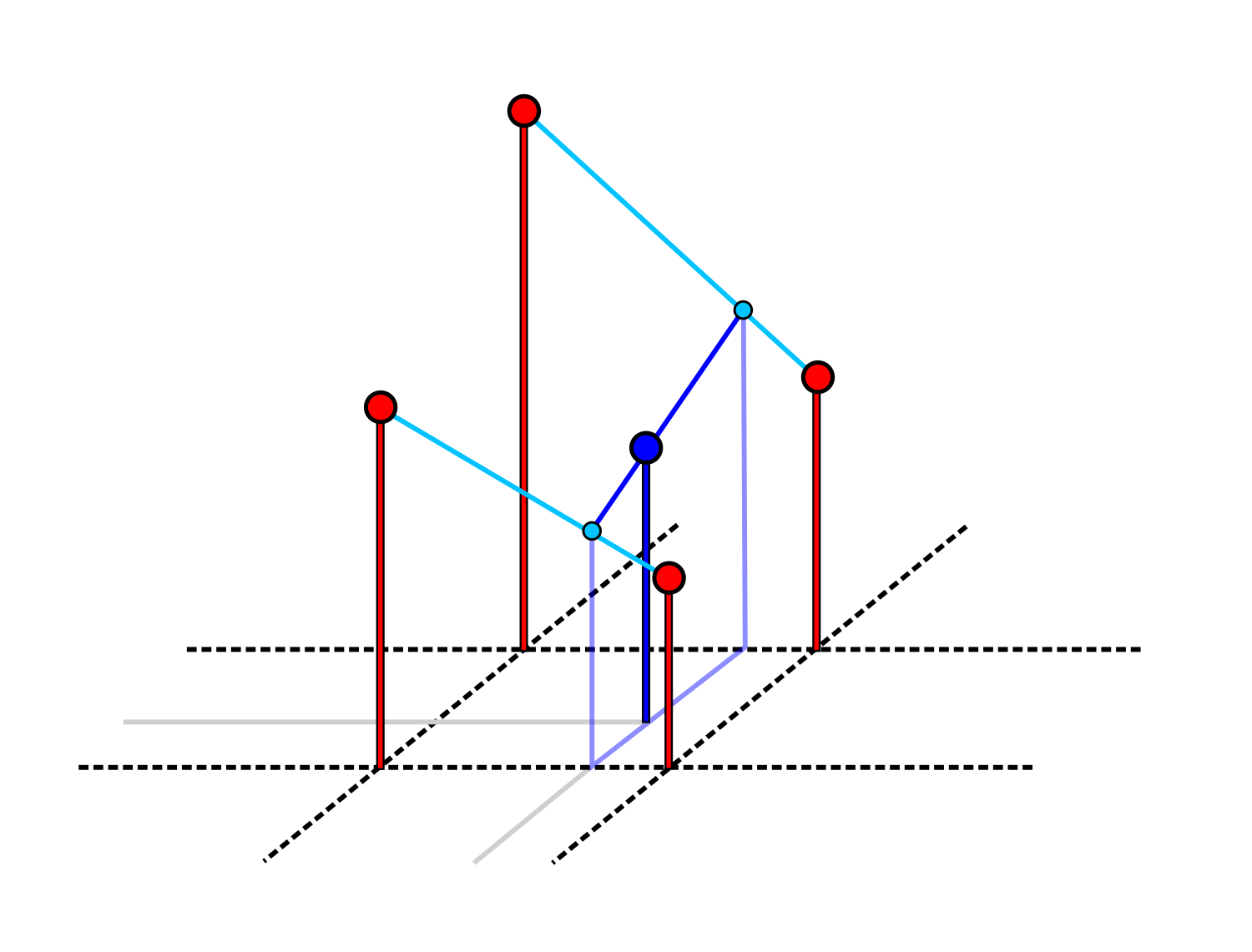
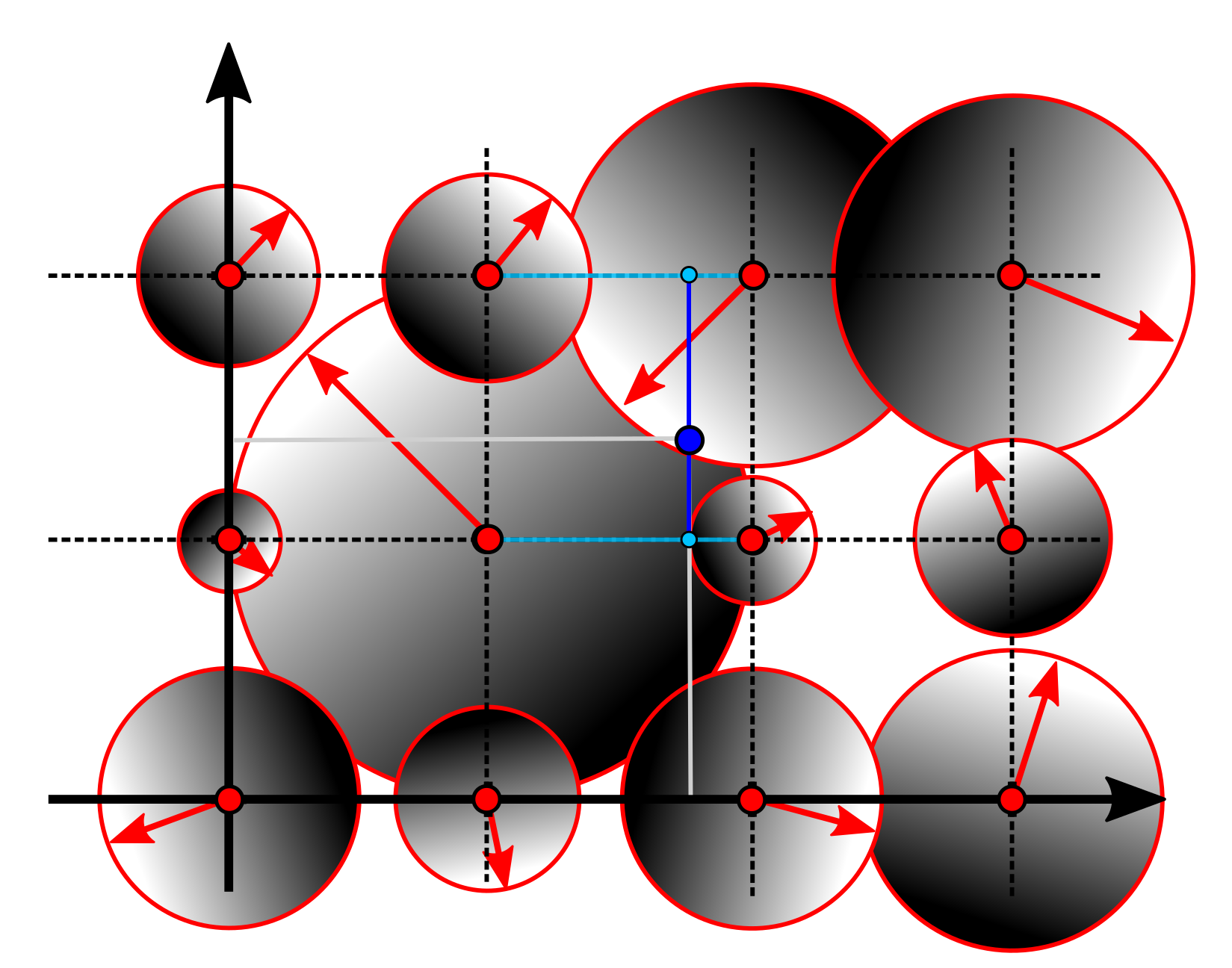
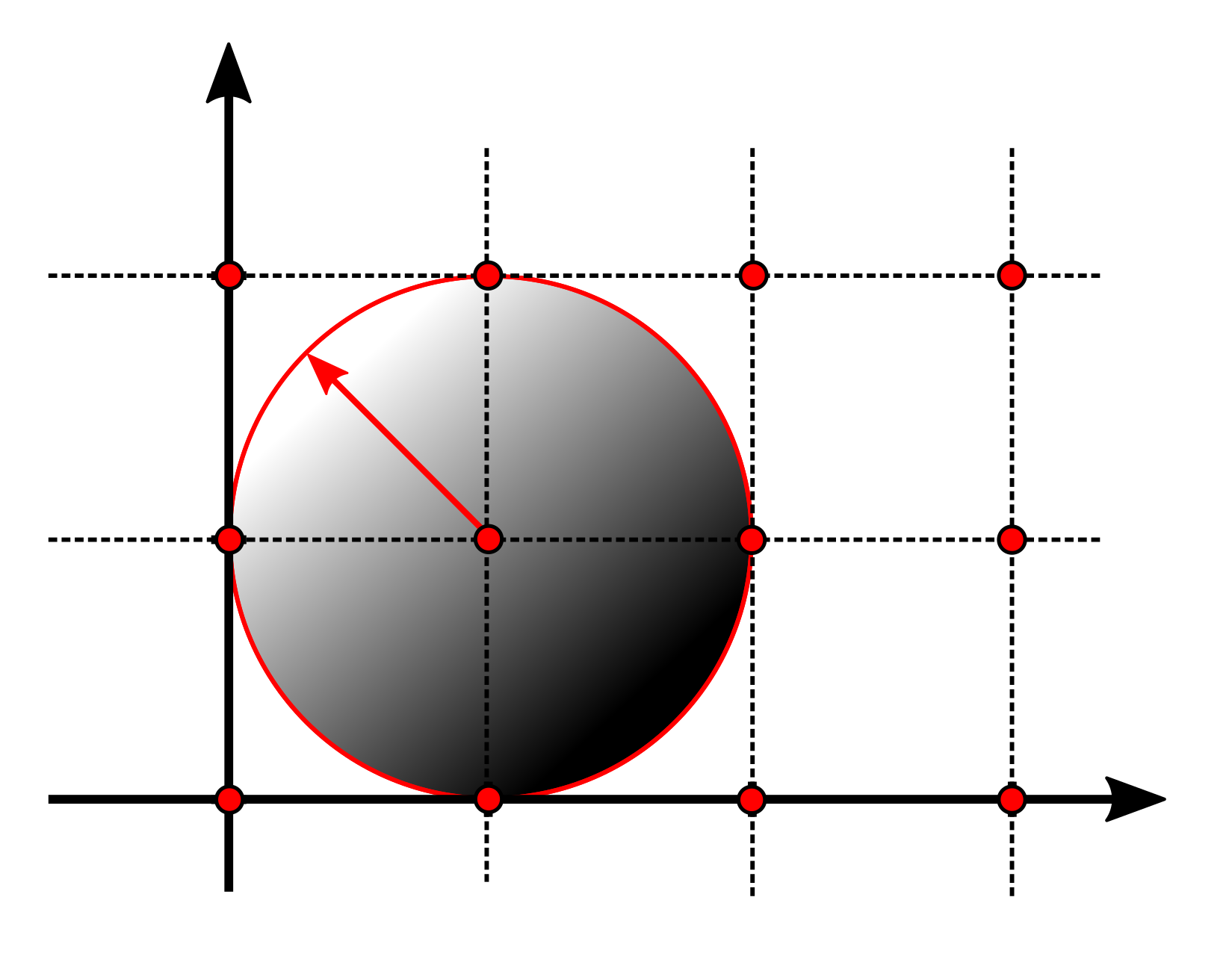
vec3 random_pcg3d(uvec3 v) {
  v = v * 1664525u + 1013904223u;
  v.x += v.y*v.z; v.y += v.z*v.x; v.z += v.x*v.y;
  v ^= v >> 16u;
  v.x += v.y*v.z; v.y += v.z*v.x; v.z += v.x*v.y;
  return vec3(v) * (1.0/float(0xffffffffu));
}
  • Die Bits des 32-Bit uvec3 werden durch Multiplikation mit großen Primzahlen durcheinander "gewürfelt"
  • Erzeugt eine gleichverteilte Zufallszahl im Bereich [0.0, 1.0]

Beispiel: Erzeugung von Pseudo-Zufallszahlen

fake_shadow

Value Noise

  • Ziel: Erzeugen eines weichen Übergangs zwischen den Zufallswerten
    • Schritt 1: Zufallswerte für Punkte auf einem groben Gitter erzeugen
    • Schritt 2: Zwischen den Punkten interpolieren, z.B. mit bilinearer Interpolation

Bilineare Interpolation

bilinear_interpolation01
$x$
$x_1$
$x_2$
$y$
$y_1$
$y_2$
grobes Gitter
Zufalls-
werte
$\mathbf{p}$

Bilineare Interpolation

bilinear_interpolation02
$x$
$x_1$
$x_2$
$y$
$y_1$
$y_2$
grobes Gitter
Zufallswerte
$\mathbf{p}$
$\mathbf{q}_1$
$f(\mathbf{q}_1) = \frac{x_2-x}{x_2-x_1} f(x_1, y_1) + \frac{x - x_1}{x_2-x_1} f(x_2, y_1)$
$\mathbf{q}_2$
$f(\mathbf{q}_2) = \frac{x_2-x}{x_2-x_1} f(x_1, y_2) + \frac{x - x_1}{x_2-x_1} f(x_2, y_2) $
$f(\mathbf{p}) = \frac{y_2-y}{y_2-y_1} f(\mathbf{q}_1) + \frac{y - y_1}{y_2-y_1} f(\mathbf{q}_2)$

Smoothstep

$\mathrm{f}(x) = 3 x^2 - 2 x^3 = x^2 (3 - 2 x)$

smoothstep
 smoothstep(0.0, 1.0, x) 

Beispiel: Value Noise

value noise

Fractal Value Noise

  • Die in der Natur beobachteten Effekte sind oft das Ergebnis mehrerer Prozesse, die auf verschiedenen Skalen wirken
  • Die Idee von fraktalem Rauschen ist, dass wir Rauschen unterschiedlicher Frequenzen addieren
  • Eine gängige Wahl der Parameter ist, die Frequenz zu verdoppeln und die Amplitude für jede Ebene zu halbieren
fractal_value_noise
Amplitude: 0.500, Frequency: 4
Amplitude: 0.250, Frequency: 8
Amplitude: 0.125, Frequency: 16

Gradient Noise

  • Pro Gitterpunkt wird ein zufälliger Gradientenvektor erzeugt
  • Der Wert für einen Punkt $\mathbf{p}$ zwischen den Gitterpunkten wird interpoliert
gradient_interpolation01
$x$
$x_1$
$x_2$
$y$
$y_1$
$y_2$
$\mathbf{p}$

Gradient Noise

  • Der Wert für einen Punkt $\mathbf{p}$ ergibt sich aus dem Skalarprodukt zwischen dem Gradientenvektor (rot) und dem Vektor vom Gitterpunkt zu Punkt $\mathbf{p}$ (blau)
gradient_interpolation03
dot(↖, ↗) = -0.3

Abtasten eines Einheitskreises

  • Zwei gleichverteilte Variablen $u$ und $v$ im Intervall $[0,1]$
  • $r = u, \quad \phi = 2 \pi \,v\quad\quad$
  • $r = \sqrt{u}, \quad \phi = 2 \pi \,v\quad\,$
$x$
$y$
$r$
$1.0$
$1.0$
$\phi$
$ \begin{pmatrix}x\\y\end{pmatrix} = \begin{pmatrix}r \, \cos(\phi)\\r \, \sin(\phi)\end{pmatrix}$

Beispiel: Gradient Noise

gradient noise

3D Perlin Noise

  • 3D Perlin Noise wählt zufällig 12 verschiedene Gradienten aus
  • Jeder Gradientenvektor hat eine Länge von $\sqrt{2}$
perlin_gradients
\begin{pmatrix}0\\1\\1\end{pmatrix}
\begin{pmatrix}-1\\0\\1\end{pmatrix}
\begin{pmatrix}1\\1\\0\end{pmatrix}
\begin{pmatrix}-1\\-1\\0\end{pmatrix}
\begin{pmatrix}0\\1\\-1\end{pmatrix}
\begin{pmatrix}-1\\0\\-1\end{pmatrix}

Smootherstep

$\mathrm{f}(x) = 6 x^5 - 15 x^4 + 10 x^3 = x^3\,(x\,(6x-15)+10)$

smootherstep
 smoothstep 
 smootherstep 

Gibt es Fragen?

questions

Anregungen oder Verbesserungsvorschläge können auch gerne per E-mail an mich gesendet werden: Kontakt

Weitere Vorlesungsfolien

Folien auf Englisch (Slides in English)

Impressum, Datenschutz,