Steuerungstasten

→ nächste Folie (auch Enter oder Spacebar).
← vorherige Folie
 d  schaltet das Zeichnen auf Folien ein/aus
 p  wechselt zwischen Druck- und Präsentationsansicht
CTRL  +  vergrößert die Folien
CTRL  -  verkleinert die Folien
CTRL  0  setzt die Größenänderung zurück

Das Weiterschalten der Folien kann ebenfalls durch das Klicken auf den rechten bzw. linken Folienrand erfolgen.

Notation

Typ Schriftart Beispiele
Variablen (Skalare) kursiv $a, b, x, y$
Funktionen aufrecht $\mathrm{f}, \mathrm{g}(x), \mathrm{max}(x)$
Vektoren fett, Elemente zeilenweise $\mathbf{a}, \mathbf{b}= \begin{pmatrix}x\\y\end{pmatrix} = (x, y)^\top,$ $\mathbf{B}=(x, y, z)^\top$
Matrizen Schreibmaschine $\mathtt{A}, \mathtt{B}= \begin{bmatrix}a & b\\c & d\end{bmatrix}$
Mengen kalligrafisch $\mathcal{A}, \{a, b\} \in \mathcal{B}$
Zahlenbereiche, Koordinatenräume doppelt gestrichen $\mathbb{N}, \mathbb{Z}, \mathbb{R}^2, \mathbb{R}^3$

Reflexionen

  • Um spiegelnde oder glänzende Oberfläche zu modellieren reichen die bisher verwendeten lokalen Beleuchtungsmodelle nicht aus
  • Die lokalen Beleuchtungsmodelle approximieren das einfallende Licht mit einer (oder mehreren) Lichtquellen. Sie vernachlässigen jedoch, dass Licht ebenfalls von anderen Oberflächen reflektiert werden kann bevor es auf den gerade betracheten Oberflächenpunkt trifft
  • Für spiegelnden oder glänzenden Oberfläche liefert die lokalen Beleuchtungsmodelle allein keine überzeugenden Ergebnisse, da die reflektieren Objekte nicht sichtbar sind

Reflexionsgesetz

  • Einfallswinkel $\theta_i$ = Ausfallswinkel $\theta_r$
  • Bei gegebener Oberflächennormalen $\mathbf{n}$ berechnet sich der reflektierte Stahl $\mathbf{\omega}_r$ aus dem einfallendem Stahl $\mathbf{\omega}_i$ gemäß:

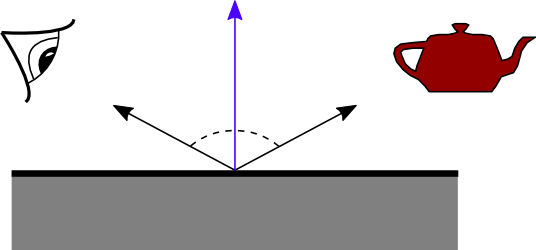
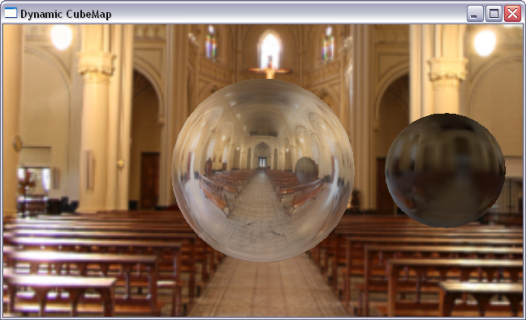
    $\mathbf{\omega}_r = 2 (\mathbf{\omega}_i^{\top} \mathbf{n}) \mathbf{n} - \mathbf{\omega}_i$

reflect
$\mathbf{\omega}_r$
$\mathbf{\omega}_i$
$\theta_i$
$\theta_r$
$\mathbf{n}$

Approximation der Reflexion

  • Der Winkel indem ein Betrachter auf einen Oberflächenpunkt schaut ist bei einer dynamischen Szene typischerweise nicht bekannt
  • Zur exakten Berechnung der Reflexion, muss in jedem Oberflächenpunkt alle möglichen einfallenden Stahlen $\mathbf{\omega}_i$ vorgehalten (bzw. berechnet) werden
  • Da dies extrem speicheraufwendig (bzw. rechenaufwendig) wäre (4-dimensionale Funktion pro Oberflächenpunkt), wird stattdessen eine Approximation verwendet
  • Idee: Alle einfallenden Stahlen werden nur für einen repräsentativen Punkt eines Objekts gespeichtert

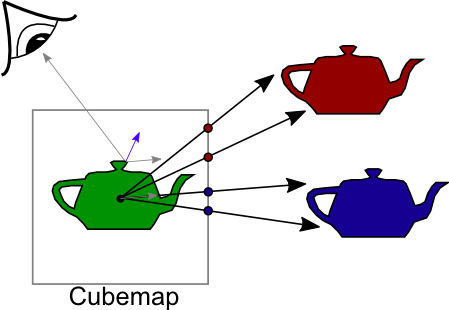
Cubemap

  • Eine Möglichkeit zur Speicherung alle möglichen einfallenden Stahlen $\mathbf{\omega}_i$ ist die Verwendung einer Cubemap (oder einer Spheremap)
  • Dazu wird ein Würfel um den gewählten repräsentativen Punkt gelegt und die einfallende Leuchtdichte abgelegt
  • Zur Berechung des Beitrags der Reflexion, wird die Reflexionsrichtung mittels der Oberflächennormalen des betrachteten Punkts berechnet und diese Richtung in der Cubemap nachgeschlagen
cubemap

Environment-Lighting

  • Idee: Bilder einer realen Umgebung können verwendet werden, um virtuelle Objekte zu beleuchten
  • Dazu werden viele einzelne Aufnahmen einer rotierenden Kamera verwendet, um die Cubemap bzw. Spheremap der Umgebung zu erstellen
cubemap
Quelle: Luis Argerich, Creative Commons License

Spheremap der realen Umgebung

Cubemap der realen Umgebung

Erzeugung einer Cubemap in OpenGL

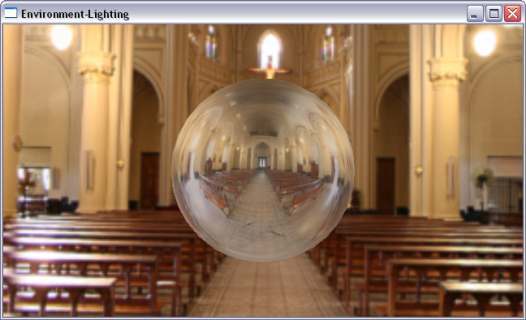
  • Eine Cubemap ist eine spezielle Textur, die mit dem Target GL_TEXTURE_CUBE_MAP gekennzeichnet wird: 
    GLuint textureID;
glGenTextures( 1, &textureID);
glBindTexture(GL_TEXTURE_CUBE_MAP, textureID);
  • Die Cubemap besteht aus sechs 2D Bildern (für jede Seite des Würfels eins), wobei die Bilddaten folgendermaßen übergeben werden: 
    glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X, ..., imgData1);
glTexImage2D(GL_TEXTURE_CUBE_MAP_NEGATIVE_X, ..., imgData2);
glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_Y, ..., imgData3);
glTexImage2D(GL_TEXTURE_CUBE_MAP_NEGATIVE_Y, ..., imgData4);
glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_Z, ..., imgData5);
glTexImage2D(GL_TEXTURE_CUBE_MAP_NEGATIVE_Z, ..., imgData6);

Erzeugung einer Cubemap in OpenGL

cubemap_RT.png
GL_TEXTURE_CUBE_MAP_POSITIVE_X		 cubemap_LF.png
GL_TEXTURE_CUBE_MAP_NEGATIVE_X
cubemap_UP.png
GL_TEXTURE_CUBE_MAP_POSITIVE_Y		 cubemap_DN.png
GL_TEXTURE_CUBE_MAP_NEGATIVE_Y
cubemap_BK.png
GL_TEXTURE_CUBE_MAP_POSITIVE_Z		 cubemap_FR.png
GL_TEXTURE_CUBE_MAP_NEGATIVE_Z

Beispiel: Environment-Lighting mittels Cubemaps

opengl_envlight

Beispiel: Environment-Lighting mittels Cubemaps

Vertex Shader: 
#version 140
in vec3 inputPosition;
in vec2 inputTexCoord;
in vec3 inputNormal;
uniform mat4 projection, view, modelTrans, normalMat;
out vec3 normalInterp;
out vec3 vertPos;

void main(){
    gl_Position = projection * view * modelTrans *
                  vec4(inputPosition, 1.0);
    vec4 vertPos4 =  modelTrans * vec4(inputPosition, 1.0);
    vertPos = vec3(vertPos4) / vertPos4.w;
    normalInterp = vec3(normalMat * vec4(inputNormal, 0.0));
}

Beispiel: Environment-Lighting mittels Cubemaps

Fragment Shader: 
#version 140
 
in vec3 normalInterp;
in vec3 vertPos;

out vec4 outputColor;

uniform samplerCube myTexture;
uniform int mode;
uniform vec3 eyePos;

const vec3 baseColor = vec3(0.4, 0.4, 0.4);

void main() {
  vec3 normal = normalize(normalInterp);
  vec3 diffuseColor = vec3(textureLod(myTexture, normal, 5));
  vec3 viewDir = vertPos - eyePos;
  vec3 r = reflect(viewDir, normal);
  // also try the following to generate refraction
  // vec3 r = refract(viewDir, normal,0.95);
  vec3 specColor = vec3(texture(myTexture,normalize(r)));

  float diffuseMix = 0.7;
  float specMix = 0.5;

  // no diffuse, no spec
  if(mode == 2) {
    diffuseMix = 0.0;
    specMix = 0.0;
  }

  // only diffuse
  if(mode == 3) {
    diffuseMix = 1.0;
    specMix = 0.0;
  }

  // only specular
  if(mode == 4) {
    diffuseMix = 0.0;
    specMix = 1.0;
  }

  vec3 color = mix(baseColor,diffuseColor*baseColor,diffuseMix);
  color = mix(color, specColor + color, specMix);

  outputColor = vec4(color, 1.0);
}

Dynamische Erzeugung einer Cubemap

  • Eine Cubemap der Umgebung kann auch dynamisch erzeugt werden, so dass z.B. Reflexionen von bewegten Objekten richtig dargestellt werden
  • Dazu wird die Szene sechs mal gerendert (jeweils einmal für jede Seite des Würfels) und die Kameraparameter für jeden Renderdurchgang entsprechend gesetzt (Kamera mit Öffnungswinkel von 90 Grad blickt in +X, -X, +Y, -Y, +Z und -Z-Richtung)
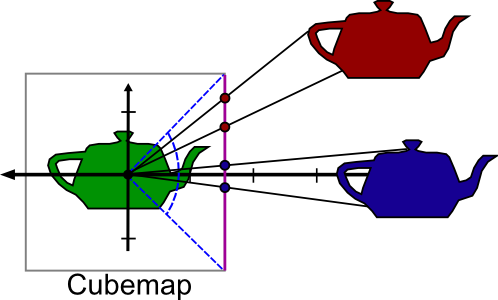
dyncubemap

Beispiel: Dynamische Cubemaps

opengl_dynamiccubemap

Gibt es Fragen?

questions

Anregungen oder Verbesserungsvorschläge können auch gerne per E-mail an mich gesendet werden: Kontakt

Weitere Vorlesungsfolien

Folien auf Englisch (Slides in English)

Impressum, Datenschutz,