Grafikprogrammierung
2D Objekte: Vektor- und Rastergrafik

Das Weiterschalten der Folien kann ebenfalls durch das Klicken auf den rechten bzw. linken Folienrand erfolgen.

• Wenn Koordinaten von 2D- oder 3D-Formen in der Computergrafik mathematisch definiert werden, geschieht dies idealerweise durch reelle Zahlen (die im Computer als Gleitkommazahl repräsentiert werden)
• Beispiel: Ein Punkt in einem 2D-Koordinatensystem kann durch zwei reelle Zahlen $x=4.5$ und $y=2.33$ definiert werden

$x$-Koordinate

$y$-Koordinate

Punkt $\mathbf{p}$

• Eine Repräsentation von 2D- oder 3D-Formen mit reellen Koordinaten wird als Vektorgrafik bezeichnet
• Der Begriff ergibt sich daraus, dass die Koordinaten als Vektoren geschrieben werden können
• Für einen Punkt $\mathbf{p}$ in einem 2D-Koordinatensystem beispielsweise
  
  $\mathbf{p}=\begin{pmatrix} x\\y\end{pmatrix} = \begin{pmatrix} 4.5\\2.33\end{pmatrix}$

• In der Vektorgrafik werden die Objekte durch Kombination von Basisobjekten (wie z.B. Linie, Rechteck, Kreis, Dreieck, Polygon) beschrieben

$x$-Koordinate

$y$-Koordinate

Dreieck

Rechteck

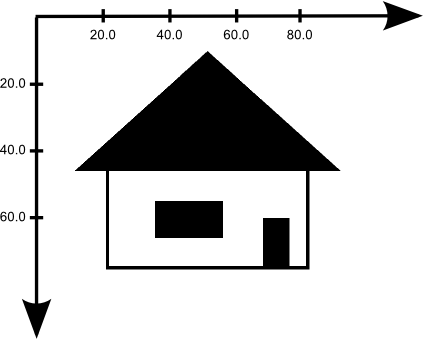
public void paint(Graphics g) {
  Graphics2D g2d = (Graphics2D) g; // cast to Graphics2D
  g2d.draw(new Rectangle2D.Double(20.75, 45.0, 60.0, 30.00) );
  g2d.fill(new Rectangle2D.Double(67.33, 60.0,  8.0, 15.00) ); 
  g2d.fill(new Rectangle2D.Double(35.00, 55.0, 20.3, 11.00) );
  GeneralPath triangle = new GeneralPath(); 
  triangle.moveTo(10.75, 46.0);
  triangle.lineTo(90.75, 46.0);
  triangle.lineTo(50.75, 10.0);
  triangle.closePath();
  g2d.fill(triangle);
 }

Vollständiger Quelltext:
House2D.java

• Eine Repräsentation als Vektorgrafik hat den Vorteil, dass die Objekte beliebig vergrößert oder verkleinert werden können
• Ein analoger Plotter beispielsweise kann die Koordinaten genau anfahren und so ein sehr genaues Abbild der Formen zeichnen

Weltkarte

Ausschnittsvergrößerung

Zum Erstellen von 2D-Vektorgrafiken gibt es zahlreiche freie und kommerzielle Programme:

• Inkscape
• Xfig
• OpenOffice Draw
• Adobe Illustrator
• Corel Draw
• Microsoft PowerPoint
• ...

Beliebte Dateiformate zum Speichern von 2D-Vektorgrafiken sind:

• Scalable Vector Graphics (SVG)
• PostScript (PS)
• Portable Document Format (PDF)
• Windows Metafile (WMF)
• ...

• Die heutigen Bildschirme stellen einzelne Bildelemente dar (Pixel="Picture Elements"), die auf einem festen Raster angeordnet sind
• Drucker mit linearem Papiervorschub (keine Plotter) tragen Farbe ebenfalls mit diskreten Punktrastern auf
• Rastergrafiken besitzen einen Farbwert für jedes Pixel ihres Rasters. Sie sind daher vollständig definiert durch:
  • Bildbreite: Anzahl der Pixel in x-Richtung
  • Bildhöhe: Anzahl der Pixel in y-Richtung
  • und einem Datenfeld mit (Breite x Höhe) Farbwerten

• Hier ein Beispiel für eine Rastergrafik mit 9 x 6 Pixeln (Zählung beginnt bei 0)
• Im Folgenden wird angenommen, dass das Pixelraster durch die Mitte der Pixelfläche verläuft

$x$-Koordinate

$y$-Koordinate

Pixelfläche

Pixelraster

Außenkante der Rastergrafik

• Digitale Bilder sind typische Beispiele für eine Rastergrafik
• Bilddaten von realen Objekten werden z.B. mit einer Digitalkamera mit lichtempfindlichen Pixelflächen erfasst
  • 1280 × 1024 (1,3 Megapixel)
  • 2560 × 2048 (5,2 Megapixel)
  • 5120 × 4096 (21 Megapixel)
• Typische Konventionen bei Rastergrafiken:
  • Zählung der Pixel beginnt bei 0
  • $x$-Koordinatenachse nach rechts
  • $y$-Koordinatennachse nach unten

class RasterImage {
  protected int imageWidth;
  protected int imageHeight;
  protected int[] imageData;
  
  public RasterImage(int width, int height) { 
    imageData = new int[width*height]; ...
  }
  public int getPixel(int x, int y) { 
    return imageData[y*imageWidth+x];
  }
  public void setPixel(int pixelValue, int x, int y) { 
    imageData[y*imageWidth+x] = pixelValue;
  }
  ...
};

template<typename T> class RasterImage {
  protected:
    unsigned imageWidth;
    unsigned imageHeight;
    T* imageData;
  public:
    RasterImage(unsigned width, unsigned height) { 
      imageData = new T[width*height]; ...
    }
    const T getPixel(unsigned x, unsigned y) const { 
      return imageData[y*imageWidth+x];
    }
    void setPixel(T pixelValue, unsigned x, unsigned y) { 
      imageData[y*imageWidth+x] = pixelValue;
    }
    ...
};

MyPaintPanel extends JPanel {
  private BufferedImage img = null;
  public void createGUI() {
    try { img = ImageIO.read(new File("./horse.jpg")); } 
    catch (IOException e) { System.out.println("failed to load image"); }
    ...
  }
  public void paint(Graphics g) {
    super.paint(g); Graphics2D g2d = (Graphics2D) g;
    int oldRgb = img.getRGB(10, 100); // read a pixel
    int rgb = 0xFFFF0000; // Alpha-Red-Green-Blue
    img.setRGB(10, 100, rgb); // draw red pixel
    g.drawImage(img, 0, 0, null);
  }
}

Quelltext des Beispiels: MyBufferedImage.java

• Sehr geeignet für komplexe Szenen mit unregelmäßigen Formen oder vielen Farben
• Speicherbedarf ist unabhängig von der Szenenkomplexität
• Direkte Darstellung auf heutigen Bildschirmen

• Bei der Darstellung sehr einfacher Objekte ist der Speicherbedarf im Vergleich zu einer Vektorgrafik höher
• Bei starker Vergrößerung werden einzelne Pixel erkennbar
• Dieser Effekt wird auch Treppeneffekt oder Aliasing genannt

Ausschnittsvergrößerung Vektorgrafik

Ausschnittsvergrößerung Rastergrafik

Es gibt zahlreiche freie und kommerzielle Bildbearbeitungsprogramme:

• Gimp
• Microsoft Paint
• Adobe Photoshop
• Corel Photo-Paint
• ...

Beliebte Dateiformate für Rastergrafiken sind:

• PNG (Portable Network Graphics), verlustfreie Kompression
• JPEG, kleinere Dateien, da verlustbehaftete Kompression
• TIFF (Tagged Image File Format), typischerweise verlustfreie Kompression, hohe Farbtiefe (bis 32 bit)
• TGA (Targa Image File), unkomprimiert oder verlustfreie Kompression
• GIF (Graphics Interchange Format), verlustfreie Kompression, erlaubt Animationssequenzen

Anregungen oder Verbesserungsvorschläge können auch gerne per E-mail an mich gesendet werden: Kontakt

Weitere Vorlesungsfolien

Folien auf Englisch (Slides in English)