Steuerungstasten

→ nächste Folie (auch Enter oder Spacebar).
← vorherige Folie
 d  schaltet das Zeichnen auf Folien ein/aus
 p  wechselt zwischen Druck- und Präsentationsansicht
CTRL  +  vergrößert die Folien
CTRL  -  verkleinert die Folien
CTRL  0  setzt die Größenänderung zurück

Das Weiterschalten der Folien kann ebenfalls durch das Klicken auf den rechten bzw. linken Folienrand erfolgen.

Notation

Typ Schriftart Beispiele
Variablen (Skalare) kursiv $a, b, x, y$
Funktionen aufrecht $\mathrm{f}, \mathrm{g}(x), \mathrm{max}(x)$
Vektoren fett, Elemente zeilenweise $\mathbf{a}, \mathbf{b}= \begin{pmatrix}x\\y\end{pmatrix} = (x, y)^\top,$ $\mathbf{B}=(x, y, z)^\top$
Matrizen Schreibmaschine $\mathtt{A}, \mathtt{B}= \begin{bmatrix}a & b\\c & d\end{bmatrix}$
Mengen kalligrafisch $\mathcal{A}, B=\{a, b\}, b \in \mathcal{B}$
Zahlenbereiche, Koordinatenräume doppelt gestrichen $\mathbb{N}, \mathbb{Z}, \mathbb{R}^2, \mathbb{R}^3$

Mathematische Grundlagen

Skalarprodukt

scalarproduct
$\mathbf{a}$
$\mathbf{b}$
$\alpha$
$\mathbf{a}_{\mathbf{b}}$
  • Das Skalarprodukt verknüpft zwei Vektoren $\mathbf{a}$ und $\mathbf{b} \in \mathbb{R}^N$. Ergebnis ist ein Skalar.
  • Skalarprodukt: $\langle \mathbf{a} \cdot \mathbf{b}\rangle = \mathbf{a}^\top \mathbf{b} = \sum\limits_{i=1}^N a_i b_i$
  • Skalarprodukt im $\mathbb{R}^3$: $\mathbf{a}^\top \mathbf{b} = (a_1, a_2, a_3) \begin{pmatrix}b_1\\b_2 \\ b_3 \end{pmatrix} = a_1 b_1 + a_2 b_2 + a_3 b_3$
  • Kommutativ: $\langle \mathbf{a} \cdot \mathbf{b}\rangle = \langle \mathbf{b} \cdot \mathbf{a}\rangle$
  • Kosinusgesetz: $\langle \mathbf{a} \cdot \mathbf{b}\rangle = |\mathbf{a}| |\mathbf{b}| \cos \alpha$
  • Orthogonale Vektoren: $\mathbf{a} \perp \mathbf{b} \rightarrow \langle \mathbf{a} \cdot \mathbf{b}\rangle = 0$
  • Senkrechte Projektion: $\mathbf{a}_{\mathbf{b}} = (\mathbf{a}^\top \frac{\mathbf{b}}{|\mathbf{b}| }) \frac{\mathbf{b}}{|\mathbf{b}| }$
  • Verbindung zur Matrixmultiplikation:
    $\begin{bmatrix}a_{11} & a_{12}\\a_{21} & a_{22}\end{bmatrix}\begin{bmatrix}b_{11} & b_{12}\\b_{21} & b_{22}\end{bmatrix} = \begin{bmatrix}\mathbf{a}_1^\top\\ \mathbf{a}_2^\top\end{bmatrix}\begin{bmatrix}\mathbf{b}_1 & \mathbf{b}_2\end{bmatrix} = \begin{bmatrix}\mathbf{a}_1^\top\mathbf{b}_1 & \mathbf{a}_1^\top\mathbf{b}_2\\ \mathbf{a}_2^\top\mathbf{b}_1 & \mathbf{a}_2^\top\mathbf{b}_2 \end{bmatrix}$

Kreuzprodukt

scalarproduct
$\mathbf{a}$
$\mathbf{b}$
$\alpha$
$\mathbf{a} \times \mathbf{b}$
$|\mathbf{a} \times \mathbf{b}|$
  • Das Kreuzprodukt verknüpft zwei Vektoren $\mathbf{a}$ und $\mathbf{b} \in \mathbb{R}^3$. Ergebnis ist ein neuer Vektor $\mathbf{c} = \mathbf{a} \times \mathbf{b} \in \mathbb{R}^3$.
  • Kreuzprodukt: $\begin{pmatrix}a_1\\a_2 \\ a_3 \end{pmatrix} \times \begin{pmatrix}b_1\\b_2 \\ b_3 \end{pmatrix} = \begin{pmatrix}a_2 b_3 - a_3 b_2\\ a_3 b_1 - a_1 b_3 \\ a_1 b_2 - a_2 b_1 \end{pmatrix}$
  • Matrixschreibweise: $\mathbf{a} \times \mathbf{b} = \begin{bmatrix}0 & -a_3 & a_2 \\a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{bmatrix} \mathbf{b} = [\mathbf{a}]_\times \,\mathbf{b}$
  • Antisymmetrie: $\mathbf{a} \times \mathbf{b} = -\mathbf{b} \times \mathbf{a}$
  • Sinusgesetz: $|\mathbf{a} \times \mathbf{b}| = |\mathbf{a}| |\mathbf{b}| \sin \alpha$
  • Orthogonale Vektoren: $\mathbf{a} \perp (\mathbf{a} \times \mathbf{b}) \perp \mathbf{b}$

Rasterkonvertierung

Raster Conversion

  • Vektorgrafiken haben den Vorteil, dass weder Auflösung noch Bildausschnitt festgesetzt sind und jederzeit geändert werden können
  • Letztendlich muss eine Vektorgrafik jedoch in der Regel für die Darstellung in eine Rastergrafik konvertiert werden
  • Da die Rasterauflösung erst bei der Konvertierung festgesetzt werden muss, kann die Auflösung an das Ausgabegerät angepasst werden
  • D.h. bei eine Repräsentation durch eine Vektorgrafik kann ein Drucker oder Bildschirm so immer seine maximalen Auflösung erreichen

Rasterkonvertierung von Linien

  • In dieser Demonstration wird eine Linie (Geradensegment) im Vektorformat in eine sehr grobe Rastergrafik konvertiert
  • Die Endpunkte der Linie können mit der Maus interaktiv verschoben werden

Geradengleichung aus zwei Punkten

gegeben: $\mathbf{p}_0 = (x_0, y_0)^\top, \mathbf{p}_1 = (x_1, y_1)^\top$

gesucht: Geradengleichung $\mathrm{g}(\mathbf{p})$ mit $\mathbf{p}= (x, y)^\top$

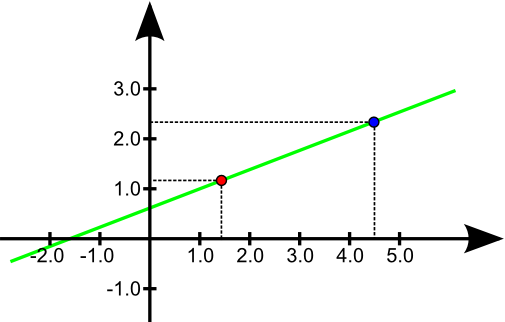
lineani1
$x$-Koordinate
$y$-Koordinate
$\mathbf{p}_0$
$\mathbf{p}_1$
lineani2
$\mathbf{p}$

aus Zeichung: $\frac{y-y_0}{x-x_0} = \frac{y_1-y_0}{x_1-x_0}$

Geradengleichung aus zwei Punkten

\begin{aligned} \frac{y-y_0}{x-x_0} &= \frac{y_1-y_0}{x_1-x_0} \\ y-y_0 &= \underbrace{\frac{y_1-y_0}{x_1-x_0}}_{m} \, \, (x-x_0) \\ y&= m \, (x - x_0) + y_0\\ y &= m \, x \, \underbrace{- \, m \, x_0 + y_0}_{b}\\ y &= m \, x + b\\ \end{aligned}

Rasterkonvertierung von Linien: Ein erster Versuch

void drawLine(int x0, int y0, int x1, int y1) {
  int dx = x1 - x0;
  int dy = y1 - y0;
  float m = dy / dx;
  for(int x = x0; x <= x1; x++) {
    float y = m * (x - x0) + y0;
    setPixel(x, round(y));  
  }
}
 
 void drawLineFloat(float x0, float y0, float x1, float y1) {
   drawLine(round(x0), round(y0), round(x1), round(y1)) ;
 }

Funktioniert alles?

  • In dieser Demonstration können die Endpunkte der Linie mit der Maus interaktiv verschoben werden

Probleme mit dem ersten Versuch

Problem 1: Funktioniert nur für $x_1 > x_0$

Lösung: Punkte tauschen, wenn $x_1 < x_0$, einzelnes Pixel zeichnen wenn $x_1 = x_0$.
 

Problem 2: Lücken in der Linie, wenn Betrag von $\Delta_y = y_1-y_0$ größer als Betrag von $\Delta_x = x_1-x_0$

Lösung: Die Lücken entstehen, da die Schleife über $x$ läuft. Daher Schleife über $y$, wenn $|\Delta_y|>|\Delta_x|$

Rasterkonvertierung von Linien: Fallunterscheidung

drawLine(int x0, int y0, int x1, int y1) {
  int dy = y1 - y0;
  int dx = x1 - x0;
  if(dx == 0 && dy ==0) { setPixel(x0, y0); return;}  
  
  if(abs(dx) >= abs(dy)) {
    if (x1 > x0) drawLineX(x0, y0, x1, y1); 
    else drawLineX(x1, y1, x0, y0);
  }else{
    if (y1 > y0) drawLineY(x0, y0, x1, y1); 
    else drawLineY(x1, y1, x0, y0);
  } 
}

void drawLineX(int x0, int y0, int x1, int y1) {
  int dy = y1 - y0;
  int dx = x1 - x0;
  float m = dy / dx;
  for(int x = x0; x <= x1; x++) {
    float y = m * (x - x0) + y0;
    setPixel(x, round(y));  
  }
}

void drawLineY(int x0, int y0, int x1, int y1) {
  int dy = y1 - y0;
  int dx = x1 - x0;
  float mInv = dx / dy;
  for(int y = y0; y <= y1; y++) {
    float x =  mInv * (y - y0) + x0;
    setPixel(round(x), y);  
  }
}

Rasterkonvertierung von Linien: Beschleunigung

  • Jeder Schleifenschritt braucht eine Multiplikation, mehrere Additionen und eine Rundung
  • Idee: inkrementeller Algorithmus spart Operationen
  • Ausgehend von der Geradengleichung $y = m \, x + b$ und mit $(x_{i+1}-x_i)=1$ (wobei $i$ den Iterationsindex angibt) gilt :

\begin{aligned} y_{i+1} &= m \, x_{i+1} + b\\ y_{i+1} &= m \, \left(x_i + (x_{i+1}-x_i)\right) +b \\ y_{i+1} &= y_i + m \,(x_{i+1}-x_i)\\ y_{i+1} &= y_i + m\\ \end{aligned}

Rasterkonvertierung von Linien: Beschleunigung

void drawLineXFaster(int x0, int y0, int x1, int y1) {
  int dy = y1 - y0;
  int dx = x1 - x0;
  float m = dy / dx;
  float y = y0;
  for(int x = x0; x <= x1; x++) {
    setPixel(x, round(y));  
    y += m;
  }
}

void drawLineYFaster(int x0, int y0, int x1, int y1) {
  int dy = y1 - y0;
  int dx = x1 - x0;
  float mInv = dx / dy;
  float x = x0;
  for(int y = y0; y <= y1; y++) {
    setPixel(round(x), y);  
    x += mInv;
  }
}

Rasterkonvertierung von Linen: Mittelpunktalgorithmus

Beobachtung von Bresenham (1965):
Wenn die Schleife in $x$-Richtung läuft und ein Pixel gezeichnet wurde, gibt es nur zwei Optionen für das nächsten Pixel:

  • Keine Erhöhung → nächstes Pixel $(x+1, y)$
  • Erhöhung um 1 → nächstes Pixel $(x+1,y+1)$

Die Entscheidung, welcher Fall vorliegt, kann durch Betrachtung des Mittelpunkts $(x+1, y+0.5)$ getroffen

  • Gerade unter Mittelpunkt → Keine Erhöhung
  • Gerade über Mittelpunkt → Erhöhung um 1
Quelle: J. E. Bresenham, Algorithm for computer control of a digital plotter, IBM Systems Journal 4, 1 (1965)

Mittelpunktalgorithmus

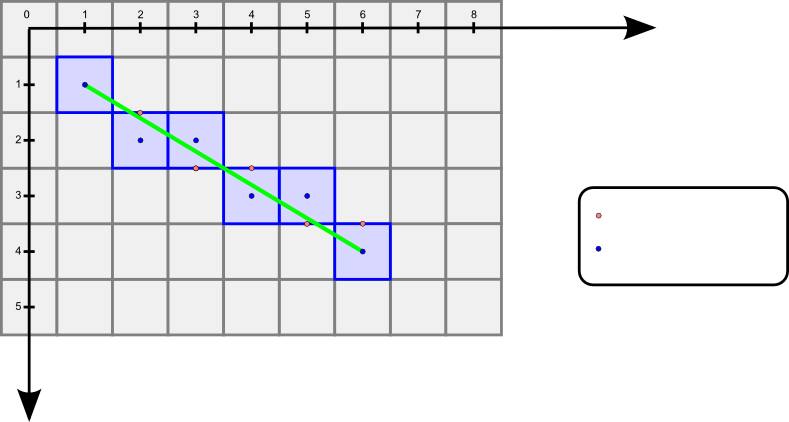
midpoint
Mittelpunkt
Pixelzentrum

Mittelpunktalgorithmus

\begin{aligned} \frac{y-y_0}{x-x_0} &= \frac{y_1-y_0}{x_1-x_0} \\ (y-y_0)\, \underbrace{(x_1-x_0)}_{\Delta_x}&= \underbrace{(y_1-y_0)}_{\Delta_y}\, \, (x-x_0) \\ (y-y_0)\, \Delta_x&= \Delta_y\, \, (x-x_0) \\ 0 &= \Delta_y \,x - \Delta_x \, y - \Delta_y \, x_0 + \Delta_x \, y_0 \\ \mathrm{g}(x,y) &= \underbrace{\Delta_y}_{a} \,x \, \underbrace{- \Delta_x}_{b} \, y + \underbrace{\Delta_x \, y_0 - \Delta_y \, x_0 }_{c} \\ \mathrm{g}(x,y) &= a x + b y + c \end{aligned}

Mittelpunktalgorithmus

Implizite Geradengleichung:

\begin{aligned} \mathrm{g}(x,y) &= a x + b y + c \\ \end{aligned}

  • Wenn $\mathrm{g}(x,y)=0$ → Punkt auf der Geraden
  • Wenn $\mathrm{g}(x,y) < 0$ → Punkt unterhalb der Geraden
  • Wenn $\mathrm{g}(x,y) > 0$ → Punkt oberhalb der Geraden

Mittelpunktalgorithmus:

  • Wenn $\mathrm{g}(x+1, y+0.5) \le 0$ → Keine Erhöhung
  • Wenn $\mathrm{g}(x+1, y+0.5) > 0$ → Erhöhung um 1

Mittelpunktalgorithmus

Inkrementelle Berechnung der Entscheidungsvariablen $d_{i} = \mathrm{g}(x+1, y+0.5)$:

\begin{aligned} \mathrm{g}(x,y) &= \Delta_y \,x - \Delta_x \, y \, + \underbrace{\Delta_x \, y_0 - \Delta_y \, x_0 }_{c} \\ \mathrm{g}(x+1, y+0.5) &= \Delta_y \,(x+1) - \Delta_x \, (y+0.5) + c \end{aligned}

Wenn keine Erhöhung:

\begin{aligned} \mathrm{g}(x+2, y+0.5) &= \Delta_y \,(x+2) - \Delta_x \, (y+0.5) + c \\ &= \mathrm{g}(x+1, y+0.5) + \Delta_y \\ d_{i+1} &= d_i + \Delta_y \end{aligned}

Wenn Erhöhung um 1 :

\begin{aligned} \mathrm{g}(x+2, y+1.5) &= \Delta_y \,(x+2) - \Delta_x \, (y+1.5) + c \\ &= \mathrm{g}(x+1, y+0.5) + \Delta_y - \Delta_x\\ d_{i+1} &= d_i + \Delta_y - \Delta_x \end{aligned}

Mittelpunktalgorithmus

Zusätzlich wird noch der initiale Wert $d_0$ der Entscheidungsvariablen benötigt:

\begin{aligned} d_0 &= \mathrm{g}(x_0+1, y_0+0.5)\\ &= \Delta_y \,(x_0+1) - \Delta_x \, (y_0+0.5) + c\\ &= \Delta_y \,x_0 + \Delta_y - \Delta_x \, y_0 - 0.5 \Delta_x + c\\ &= \Delta_y \,x_0 - \Delta_x \, y_0 + \Delta_y - 0.5 \Delta_x + c\\ &= \underbrace{\mathrm{g}(x_0, y_0)}_{=0} + \Delta_y - 0.5 \Delta_x \\ &= \Delta_y - 0.5 \Delta_x \\ \end{aligned}

Mittelpunktalgorithmus

  • Trick: Bei der Berechnung der Entscheidungsvariablen kommt es nur auf das Vorzeichen an
  • Daher kann statt $d$ auch $\hat{d}= 2 d$ als Entscheidungsvariable verwendet werden
  • Der Vorteil ist, dass dann nur Integer-Arithmetik zur Berechnung verwendet werden muss
    • Initialisierung:                  $\hat{d}_0 = 2 \Delta_y - \Delta_x$
    • Wenn keine Erhöhung: $\hat{d}_{i+1} = \hat{d}_i + 2 \Delta_y$
    • Wenn Erhöhung um 1:  $\hat{d}_{i+1} = \hat{d}_i + 2 \Delta_y - 2 \Delta_x$

Mittelpunktalgorithmus

void drawLineXEvenFaster(int x0, int y0, int x1, int y1) {
  int dx = x1 - x0; 
  int dy = abs(y1 - y0);
  int twoDx = dx + dx; 
  int twoDy = dy + dy;
  int dHat = twoDy - dx; // init decision variable 
  int incr = 1; if (y1 < y0) incr = -1; // increase or decrease y
    
  for(int x = x0, y = y0; x <= x1; x++) {
    setPixel(x, y);  
    if(dHat <= 0) { // no increment
      dHat += twoDy; 
    } else {        // increment
      dHat += twoDy - twoDx; 
      y += incr; 
    }
  }
}

void drawLineYEvenFaster(int x0, int y0, int x1, int y1) {
  int dx = abs(x1 - x0); 
  int dy = y1 - y0;
  int twoDx = dx + dx; 
  int twoDy = dy + dy;
  int dHat = twoDx - dy; // init decision variable 
  int incr = 1; if (x1 < x0) incr = -1; // increase or decrease y
  
  for(int y = y0, x = x0; y <= y1; y++) {
    setPixel(x, y);  
    if(dHat <= 0) { // no increment
      dHat += twoDx; 
    } else {        // increment 
      dHat += twoDx - twoDy; 
      x += incr; 
    }
  }
}

Mittelpunktalgorithmus für Linien

  • In dieser Demonstration können die Endpunkte der Linie mit der Maus interaktiv verschoben werden

Rasterkonvertierung von Kreisen

Rasterkonvertierung von Kreisen

Implizite Gleichung für einen Kreis mit Radius $r$:

\begin{aligned} \mathrm{g}(x,y) &= x^2 + y^2 - r^2 \\ \end{aligned}

  • Wenn $\mathrm{g}(x,y)=0$ → Punkt auf dem Kreis
  • Wenn $\mathrm{g}(x,y) < 0$ → Punkt innerhalb des Kreises
  • Wenn $\mathrm{g}(x,y) > 0$ → Punkt außerhalb des Kreises

Rasterkonvertierung von Kreisen

  • Das Vorgehen zum Zeichnen von Kreisen ist sehr ähnlich zu dem für Linien
  • Aufgrund der Symmetrie muss allerdings nur ein Achtel des Kreisumfangs berechnet werden und die anderen Pixel können kopiert werden
  • Daher wird beim Zeichnen eines Kreises auch nicht, wie bisher, eine Fallunterscheidung benötigt
  • Beim Berechnen der Kreispixel wird angenommen, dass sich der Kreis im Ursprung befindet. Das Ergebnis kann dann leicht entsprechend verschoben werden, um andere Position des Zentrums zu berücksichtigen.

Mittelpunktalgorithmus für Kreise

  • Der Mittelpunktalgorithmus für Kreise ist sehr ähnlich zu dem für Linien. Er verwendet die implizite Kreisgleichung und wertet die Position des nächsten Pixel-Mittelpunkts $(x+1, y-0.5)$ aus
  • Wird mit der for-Schleife in positive $x$-Richtung gelaufen, kann $y$ mit dem Radius initialisiert werden.
  • Damit gilt $x_\mathrm{init} = 0$ und $y_\mathrm{init} = r$

Mittelpunktalgorithmus:

  • Wenn $\mathrm{g}(x+1, y-0.5) \le 0$ → Keine Reduktion von $y$
  • Wenn $\mathrm{g}(x+1, y-0.5) > 0$ → Reduktion von $y$ um 1

Mittelpunktalgorithmus für Kreise

Inkrementelle Berechung der Entscheidungsvariablen $d_{i} = \mathrm{g}(x+1, y-0.5)$:

\begin{aligned} \mathrm{g}(x,y) &= x^2 + y^2 - r^2 \\ \mathrm{g}(x+1, y-0.5) &= (x+1)^2 + (y-0.5)^2 - r^2 = d_{i} \end{aligned}

Wenn keine Reduktion:

\begin{aligned} \mathrm{g}(x+2, y-0.5) &= (x+2)^2 + (y-0.5)^2 - r^2\\ &= (x+2)^2 + d_i - (x+1)^2\\ &= (x^2+4x+2^2) + d_i - (x^2+2x+1)\\ d_{i+1} &= d_i + 2x+ 3 \\ \end{aligned}

Wenn Reduktion um 1:

\begin{aligned} \mathrm{g}(x+2, y-1.5) &= (x+2)^2 + (y-1.5)^2 - r^2 \\ &= (x+2)^2 + (y-1.5)^2 + d_i - (x+1)^2 - (y-0.5)^2\\ d_{i+1} &= d_i + 2x - 2y + 5\\ \end{aligned}

Mittelpunktalgorithmus für Kreise

Zusätzlich wird noch der initiale Wert $d_0$ der Entscheidungsvariablen benötigt:

\begin{aligned} d_0 &= \mathrm{g}(x_0+1, y_0 + r-0.5)\\ &= \mathrm{g}(1, r-0.5)\\ &= (1)^2 + (r-0.5)^2 - r^2\\ &= 1 + r^2 -r + 0.25 - r^2\\ &= 1.25 - r \\ &= \frac{5}{4} - r\\ \end{aligned}

Mittelpunktalgorithmus für Kreise

function drawCircle(int x0, int y0, int radius) {

  int dHat = 5 - 4 * radius; // init decision variable 
  int x = 0;
  int y = radius;
  
  for(int x = 0; x <= y ; x++) {
    setSymmetricPixelCirle(x, y, x0, y0);
    if(dHat <= 0) { // no reduction of y
      dHat += 8*x + 12;
    }else {         // reduction of y by 1
      dHat += 8*x - 8*y + 20;
      y--;
    }
  }
}

Mittelpunktalgorithmus für Kreise

void setSymmetricPixelCirle(int x, int y, int x0, int y0) {
  setPixel( x+x0,  y+y0);
  setPixel(-x+x0,  y+y0);
  setPixel( x+x0, -y+y0);
  setPixel(-x+x0, -y+y0);
  setPixel( y+x0,  x+y0);
  setPixel(-y+x0,  x+y0);
  setPixel( y+x0, -x+y0);
  setPixel(-y+x0, -x+y0);
}

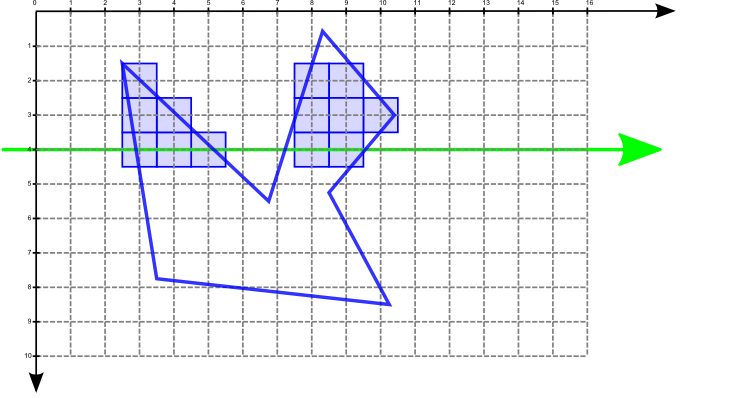
Rasterkonvertierung von Polygonen: Scanline-Algorithmus

scanline
$x$-Koordinate
$y$-Koordinate
Scanline

Rasterkonvertierung von Polygonen: Scanline-Algorithmus

  • Beim Scanline-Algorithmus wird das Pixelraster zeilenweise durchlaufen
  • Schritt 1: Für jede Zeile werden die Schnittpunkte mit den Polygonkanten berechnet
  • Schritt 2: Diese Schnittpunkte werden nach ihrer $x$-Koordinate aufsteigend sortiert
  • Schritt 3: Durchlaufe die Pixel der Scanline beginnend bei $x=0$. Zeichne Pixel nur, wenn die Parität der bisher durchlaufenen Schnittpunkte ungerade ist (Regel der ungeraden Parität)

Scanline-Algorithmus

Der Scanline-Algorithmus kann sehr effizient implementiert werden durch:

  • inkrementelles Berechnen der Schnittpunkte
  • Reduktion der betrachteten Polygonkanten pro Scanline

Scanline-Algorithmus

Dazu wird benötigt:

  1. Kanten-Datenstruktur: $\mathbf{e} = (y_\mathrm{min}, y_\mathrm{max}, x_\mathrm{hit}, m^{-1})$ 
     class Edge {
   int yMin;     // smallest value of y (when edge enters)
   int yMax;     // largest value of y (when edge leaves)
   float xHit;   // intersection point (init with x value at yMin)
   float mInv;   // dx/dy (inverse line increment)
 }
  2. Kanten-Tabelle (KT): enthält alle Kanten $(\mathbf{e}_1, ..., \mathbf{e}_k)$, sortiert nach $y_\mathrm{min}$. Bei gleichem $y_\mathrm{min}$ wird $x_\mathrm{hit}$ als zweites Sortierkriterium hinzugenommen
  3. Aktive Kanten-Tabelle (AKT): enthält alle von der aktuellen Scanline geschnittenen Kanten, sortiert nach $x_\mathrm{hit}$

Scanline-Algorithmus

Initialisiere $y = y_\mathrm{min}$ von erster Kante aus der sortierten KT
AKT = $\emptyset$ (leere Menge)
REPEAT bis AKT = $\emptyset$ und KT = $\emptyset$
  Schritt 1:
Verschiebe diejenigen Kanten von der KT in die AKT für die gilt:
$y_\mathrm{min}$ = $y$ (hereinkommende Kanten)

  Schritt 2:
Sortiere die AKT nach $x_\mathrm{hit}$

  Schritt 3:
Zeichne Pixel der aktuellen Scanline $y$ gemäß der Regel der ungeraden Parität unter Verwendung der $x_\mathrm{hit}$-Koordinaten von Kanten aus der AKT

  Schritt 4:
Entferne aus der AKT diejenigen Einträge für die gilt:
$y_\mathrm{max} = y $ (herausgehende Kanten)

  Schritt 5:
Erhöhe $y$ um 1 (nächste Scanline)

  Schritt 6:
Für jede nicht vertikale Kante in der AKT, berechne ein neues $\hat{x}_\mathrm{hit}$ mit $\hat{x}_\mathrm{hit} = x_\mathrm{hit} + m^{-1}$

END (Repeat)

Scanline-Algorithmus

Ein interaktiver Demonstrator zur Visualisierung des Scanline-Algorithmus steht auf der Webseite zur Vorlesung zur Verfügung


scanline_demo

Rasterkonvertierung von Pineda

  • Ein einfacher, parallelisierbarer Algorithmus für die Rasterkonvertierung von konvexen Polygonen wurde 1988 von Pineda vorgeschlagen
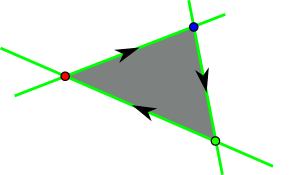
pineda_inout
aussen
aussen
innen
aussen
  • Die grundlegende Idee: Verwende die Hessesche Normalform der Geraden, die die Kanten des Polygons bilden, um zu entscheiden, ob ein Pixel innerhalb oder ausserhalb des Polygons liegt
  • Dazu wird angenommen, dass die Kanten das Polygon im Uhrzeigersinn umlaufen. Liegt ein Pixel rechts von jeder Gerade, ist es innerhalb
Quelle: Juan Pineda, A Parallel Algorithm for Polygon Rasterization, Computer Graphics, Volume 22, Number 4, 1988 (pdf)

Rasterkonvertierung von Pineda

  • Hessesche Normalform einer Geraden:
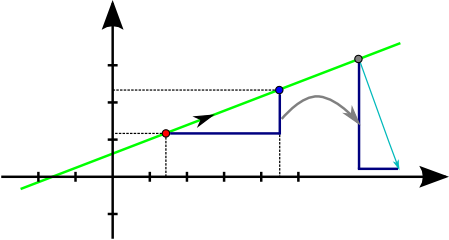
hess_normal
$\mathbf{p}$
$\mathbf{p}_0$
$\mathbf{p}_1$
$\mathbf{n}$
  • Wie aus der Zeichnung zu entnehmen, kann die Richtung der Normalen $\mathbf{n}$ aus dem gedrehten Steigungsdreieck ermittelt werden
  • Somit berechnet sich die Normale zu
    $\mathbf{n} = (n_x, n_y)^\top = (\Delta_y, -\Delta_x)^\top = (y_1-y_0, -(x_1-x_0))^\top$
  • Der Richtungsvektor $\mathbf{p} - \mathbf{p}_0$ muss senkrecht auf der Normalen stehen, d.h. es gilt
    $\mathbf{n}^\top (\mathbf{p} - \mathbf{p}_0) =0 \Leftrightarrow \mathbf{n}^\top \mathbf{p} - \mathbf{n}^\top \mathbf{p}_0 = 0$
  • Diese implizite Geradengleichung wird Hessesche Normalform genannt

Rasterkonvertierung von Pineda

  • Hessesche Normalform: Für jeden Punkt $\mathbf{p}=(x,y)^\top$ auf der Geraden gilt
    $\begin{align} \mathbf{n}^\top \mathbf{p} - \mathbf{n}^\top \mathbf{p}_0 &= 0 \\ \Leftrightarrow \frac{1}{|\mathbf{n}|}\left(\mathbf{n}^\top \mathbf{p} - \mathbf{n}^\top \mathbf{p}_0\right) &= 0\\ \Leftrightarrow a x + b y + c &= 0 \end{align}$
  • Ist die Gleichung nicht erfüllt, so liegt der Punkt $\mathbf{p}=(x,y)^\top$ nicht auf der Geraden und der Abstand ist direkt gegeben durch
    $\mathrm {d}(x,y) = \frac{1}{|\mathbf{n}|}\left(\mathbf{n}^\top \mathbf{p} - \mathbf{n}^\top \mathbf{p}_0\right)$
    pineda_inout
    aussen
    aussen
    innen
    aussen
    • Wenn $\mathrm {d}(x,y) > 0 \rightarrow$ Punkt liegt rechts
    • Wenn $\mathrm {d}(x,y) = 0 \rightarrow$ Punkt liegt auf Geraden
    • Wenn $\mathrm {d}(x,y) < 0 \rightarrow$ Punkt liegt links
  • Liegt der Pixel $\mathbf{p}=(x,y)^\top$ rechts von allen Kanten (bzw. deren Geraden), ist er innerhalb und muss gezeichnet werden, ansonsten nicht

Rasterkonvertierung von Pineda

  • Ähnlich wie beim Mittelpunktsalgorithmus, kann die Entscheidungsfunktion für jede Geradengleichung inkrementell berechnet werden.
  • Auch kommt es hier nur auf das Vorzeichen an. Da die nicht normierte Hessesche Normalform mit Integer-Arithmetik berechnet werden kann, wird diese verwendet
  • Für den ersten Pixel: $\mathrm{d}'(x,y) = \mathbf{n}^\top \mathbf{p} - \mathbf{n}^\top \mathbf{p}_0$
  • Für den nachfolgenden Pixel gilt:
    $\begin{align}\mathrm{d}'(x+1,y) &= \mathrm{d}'(x,y) + \Delta_y & \mathrm{d}'(x-1,y) &= \mathrm{d}'(x,y) - \Delta_y\\ \mathrm{d}'(x,y+1) &= \mathrm{d}'(x,y) - \Delta_x & \mathrm{d}'(x,y-1) &= \mathrm{d}'(x,y) + \Delta_x \end{align}$
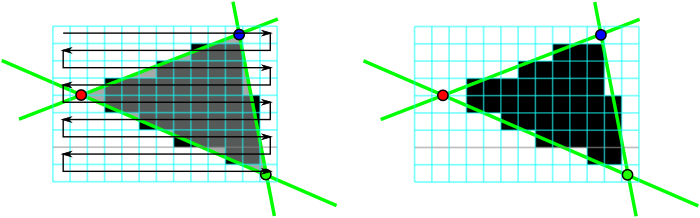
pineda_inout_raster

Rasterkonvertierung von Pineda

  • Optimierungen
    • Es müssen nur die Pixel in einem rechteckigen (das Polygon begrenzenden) Bereich betrachtet werden
    • Der rechteckige Bereich kann unterteilt werden (z.B. in 4, 8, 16, usw. Unterbereiche) und die Unterbereiche können parallel verarbeitet werden
    • Es kann eine neue Zeile begonnen werden, wenn nach mindestens einem gezeichneten Pixel das erste Pixel ausserhalb liegt (eventuell ist es nötig in der neuer Zeile die Anfangs-Kante zu suchen)
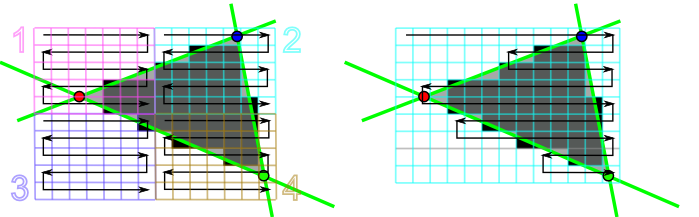
pineda_inout_raster2

Rasterkonvertierung von Pineda

Ein interaktiver Demonstrator zur Visualisierung des Pineda-Algorithmus steht auf der Webseite zur Vorlesung zur Verfügung


pineda_demo

Gibt es Fragen?

questions

Anregungen oder Verbesserungsvorschläge können auch gerne per E-mail an mich gesendet werden: Kontakt

Weitere Vorlesungsfolien

Folien auf Englisch (Slides in English)

Impressum, Datenschutz,