Image Synthesis
Intersection Shader
Thorsten Thormählen
Mai 03, 2022
Part 2, Chapter 2
Thorsten Thormählen
Mai 03, 2022
Part 2, Chapter 2
This is the print version of the slides.
Advance slides with the → key or
by clicking on the right border of the slide
Slides can also be advanced by clicking on the left or right border of the slide.
| Type | Font | Examples |
|---|---|---|
| Variables (scalars) | italics | $a, b, x, y$ |
| Functions | upright | $\mathrm{f}, \mathrm{g}(x), \mathrm{max}(x)$ |
| Vectors | bold, elements row-wise | $\mathbf{a}, \mathbf{b}= \begin{pmatrix}x\\y\end{pmatrix} = (x, y)^\top,$ $\mathbf{B}=(x, y, z)^\top$ |
| Matrices | Typewriter | $\mathtt{A}, \mathtt{B}= \begin{bmatrix}a &b\\c &d\end{bmatrix}$ |
| Sets | calligraphic | $\mathcal{A}, B=\{a, b\}, b \in \mathcal{B}$ |
| Number systems, Coordinate spaces | double-struck | $\mathbb{N}, \mathbb{Z}, \mathbb{R}^2, \mathbb{R}^3$ |
reportIntersectionEXT(...)hitAttributeEXT variable, which can be of user-defined type and
can be evaluated in the closest-hit, miss, or any-hit shader
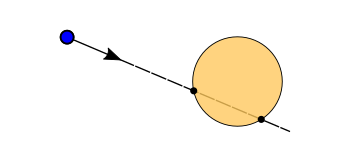

struct HitAttributeType {
vec3 normal;
vec2 texCoord;
}; // type of the "hit" variable
...
void main() { /**** INTERSECTION SHADER ****/
// ray-sphere intersection in world space
// get bounding box in object space
vec3 aabbMin;
vec3 aabbMax;
gsnGetIntersectionBox(gl_InstanceID, gl_PrimitiveID, aabbMin, aabbMax);
// transform to world space
vec3 minWorld = gl_ObjectToWorldEXT * vec4(aabbMin, 1.0);
vec3 maxWorld = gl_ObjectToWorldEXT * vec4(aabbMax, 1.0);
// center and radius of sphere in world space
vec3 center = (minWorld + maxWorld) / 2.0;
float radius = length((maxWorld - minWorld) / (sqrt(3.0) * 2.0));
vec3 b = gl_WorldRayOriginEXT - center;
vec3 r = normalize(gl_WorldRayDirectionEXT);
float p = 2.0 * dot(r, b);
float q = dot(b, b) - radius * radius;
// discriminant of the quadratic equation
float d =(p * p / 4.0) - q;
// if no solution, cancel computation
if(d < 0.0) return;
// two solutions for quadratic equation
float tin = -p / 2.0 - sqrt(d);
float tout = -p / 2.0 + sqrt(d);
// intersection at tin or tout?
float t = tout;
uint hitKind = 2u;
if(tin < tout && tin >= gl_RayTminEXT && tin <= gl_RayTmaxEXT) {
t = tin;
hitKind = 1u;
}
if(t >= gl_RayTminEXT && t <= gl_RayTmaxEXT) {
vec3 hitPoint = gl_WorldRayOriginEXT + t * gl_WorldRayDirectionEXT;
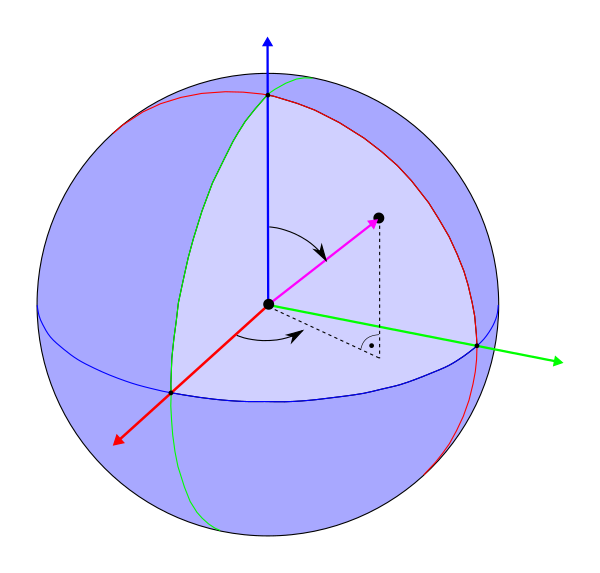
vec3 n = normalize(hitPoint - center);
vec3 localN = normalize(gl_WorldToObjectEXT * vec4(n, 0.0));
hit.normal = n;
hit.texCoord.s = fract(atan(localN.y, localN.x) / (2.0 * PI));
hit.texCoord.t = acos(-localN.z) / (PI);
reportIntersectionEXT(t, hitKind);
}
}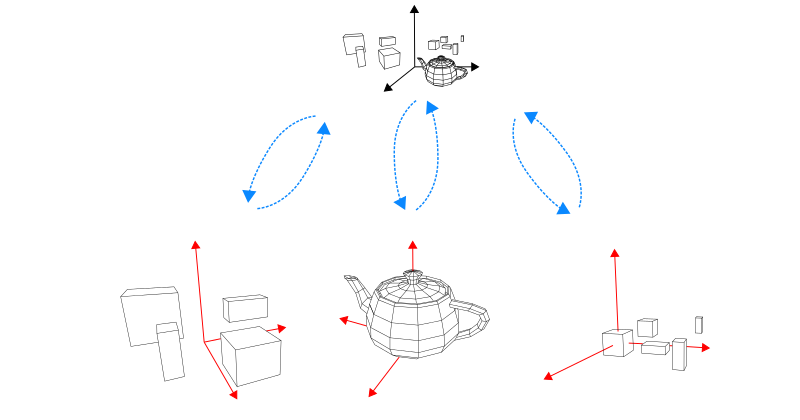
gl_ObjectToWorldEXTgl_WorldToObjectEXTgl_InstanceID = 0gl_InstanceID = 1gl_InstanceID = 2reportIntersectionEXT(...)
expects the value for $t$ in world space. In addition,
gl_RayTminEXT and
gl_RayTmaxEXT are also defined in world space.
gl_ObjectToWorldEXT is a 3 x 4 matrix,
i.e. it only contains the upper three rows of $\mathtt{T}$
gl_WorldToObjectEXT is a 3 x 4 matrix,
i.e. it only contains the upper three rows of $\mathtt{T}^{-1}$
gl_ObjectRayOriginEXT
and $\tilde{\mathbf{r}}$ by gl_ObjectRayDirectionEXTgl_WorldRayOriginEXT $\,\mathbf{s}$ and gl_WorldRayDirectionEXT $\,\mathbf{r}$
gl_ObjectRayOriginEXT $\,\tilde{\mathbf{s}}$ and gl_ObjectRayDirectionEXT $\,\tilde{\mathbf{r}}$
gl_ObjectRayDirectionEXT in the intersection shader!
struct HitAttributeType {
vec3 normal;
vec2 texCoord;
}; // type of the "hit" variable
...
void main() { /**** INTERSECTION SHADER ****/
// ray-sphere intersection in object space
// get bounding box in object space
vec3 aabbMin;
vec3 aabbMax;
gsnGetIntersectionBox(gl_InstanceID, gl_PrimitiveID, aabbMin, aabbMax);
// center and radius of sphere in object space
vec3 center = (aabbMin + aabbMax) / 2.0;
float radius = length(aabbMax.x - aabbMin.x) / 2.0;
vec3 b = gl_ObjectRayOriginEXT - center;
vec3 r = gl_ObjectRayDirectionEXT; // not normalized
float rr = dot(r, r);
float p = 2.0 * dot(r, b) / rr;
float q = (dot(b, b) - radius * radius) / rr;
// discriminant of the quadratic equation
float d =(p * p / 4.0) - q;
// if no solution, cancel computation
if(d < 0.0) return;
// two solutions for quadratic equation
float tmin = -p / 2.0 - sqrt(d);
float tmax = -p / 2.0 + sqrt(d);
// intersection at tmin or tmax?
float t = tmax;
uint hitKind = 2u;
if(tmin < tmax && tmin >= gl_RayTminEXT && tmin <= gl_RayTmaxEXT) {
t = tmin;
hitKind = 1u;
}
if(t >= gl_RayTminEXT && t <= gl_RayTmaxEXT) {
vec3 hitPoint = gl_ObjectRayOriginEXT + t * gl_ObjectRayDirectionEXT;
vec3 n = normalize(hitPoint - center);
hit.normal = n;
hit.texCoord.s = fract(atan(n.y, n.x) / (2.0 * PI));
hit.texCoord.t = acos(-n.z) / (PI);
reportIntersectionEXT(t, hitKind);
}
}
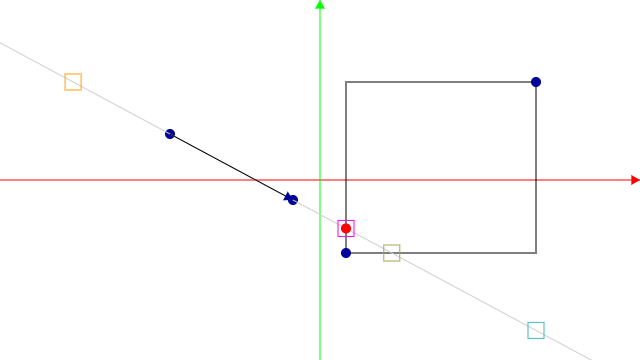
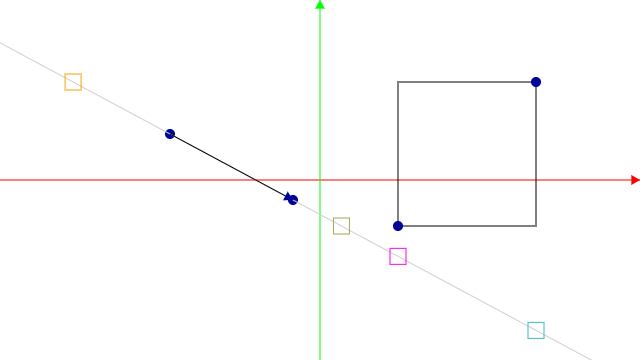
bool slabs(vec3 a, vec3 b, vec3 rayOrigin, vec3 invRayDir) {
vec3 ta = (a - rayOrigin) * invRayDir;
vec3 tb = (b - rayOrigin) * invRayDir;
vec3 tmin = min(ta, tb);
vec3 tmax = max(ta, tb);
float tin = max(max(tmin.x, tmin.y), tmin.z);
float tout = min(min(tmax.x, tmax.y), tmax.z);
return (tin <= tout);
}

struct HitAttributeType {
vec3 normal;
vec2 texCoord;
}; // type of the "hit" variable
...
void main() { /**** INTERSECTION SHADER ****/
// ray-box intersection
// get bounding box in object space
vec3 a, b;
gsnGetIntersectionBox(gl_InstanceID, gl_PrimitiveID, a, b);
// perform intersection in object space using the slab method
// Kay and Kajiya, SIGGRAPH 1986
// Majercik et al., JCGT 2018
vec3 invRayDir = 1.0 / gl_ObjectRayDirectionEXT;
vec3 ta = (a - gl_ObjectRayOriginEXT) * invRayDir;
vec3 tb = (b - gl_ObjectRayOriginEXT) * invRayDir;
vec3 tmin = min(ta, tb);
vec3 tmax = max(ta, tb);
float t_in = max(tmin.x, max(tmin.y, tmin.z));
float t_out = min(tmax.x, min(tmax.y, tmax.z));
if(t_in <= t_out) { // intersection found
// decide if first or second hit is selected
float t = t_in;
uint hitKind = 1u; // hit outside->inside
if(t < gl_RayTminEXT) {
t = t_out;
hitKind = 2u; // hit inside->outside
}
if(t >= gl_RayTminEXT && t <= gl_RayTmaxEXT) {
// compute normal and texture coordinates
vec3 center = (a + b) / 2.0;
vec3 p = gl_ObjectRayOriginEXT + t * gl_ObjectRayDirectionEXT;
vec3 n = normalize(p - center);
vec2 tc = vec2(0.0, 0.0);
vec3 n_abs = abs(n);
float max_n_abs = max(n_abs.x, max(n_abs.y, n_abs.z));
if(n_abs.x == max_n_abs) {
tc = (vec2(sign(n.x), 1.0) * p.yz - a.yz) / (b.yz - a.yz);
n = vec3(sign(n.x), 0.0, 0.0);
} else if(n_abs.y == max_n_abs) {
tc = (vec2(-sign(n.y), 1.0) * p.xz - a.xz) / (b.xz - a.xz);
n = vec3(0.0, sign(n.y), 0.0);
} else {
tc = (vec2(sign(n.z), 1.0) * p.xy - a.xy) / (b.xy - a.xy);
n = vec3(0.0, 0.0, sign(n.z));
}
hit.normal = n;
hit.texCoord = tc;
reportIntersectionEXT(t, hitKind);
}
}
}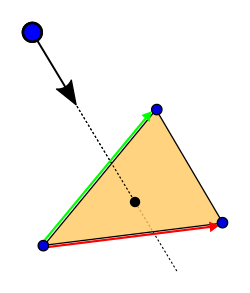
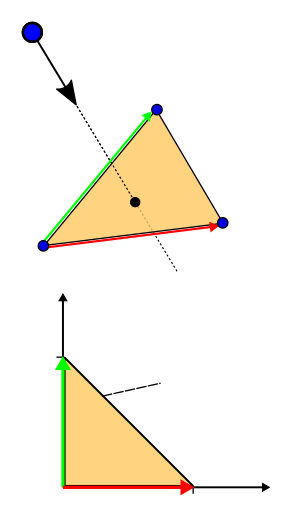
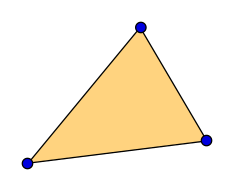

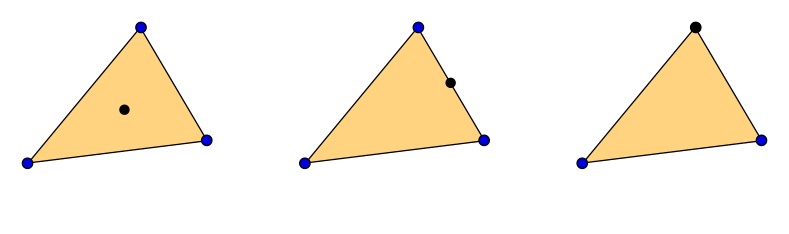
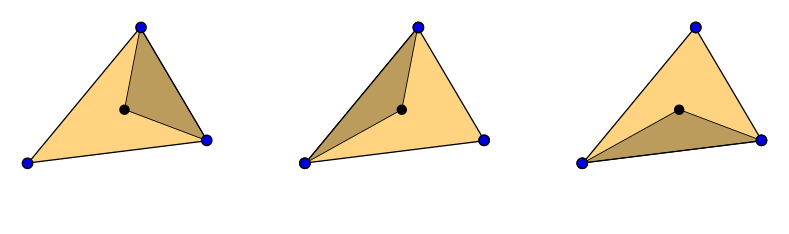
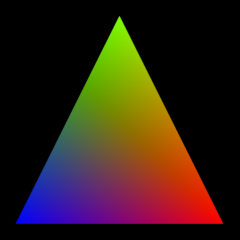
hitAttributeEXT vec2 baryCoord" variable
vec3 barys = vec3(1.0f - baryCoord.x - baryCoord.y, baryCoord.x, baryCoord.y); vec3 interpColor = blue * barys.x + red * barys.y + green * barys.z;
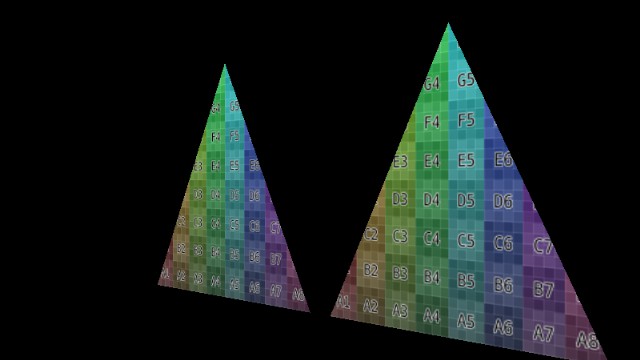
struct HitAttributeType {
vec3 normal;
vec2 texCoord;
vec2 baryCoord;
}; // type of the "hit" variable
...
void main() { /**** INTERSECTION SHADER ****/
// ray-triangle intersection
// Note: Ray-triangle intersection is a
// built-in feature of the ray tracing shader pipeline.
// It is just provided for educational purpose.
// get bounding box in object space
vec3 aabbMin;
vec3 aabbMax;
gsnGetIntersectionBox(gl_InstanceID, gl_PrimitiveID, aabbMin, aabbMax);
vec3 diff = aabbMax - aabbMin;
// a, b, and c are the three triangle vertices
vec3 a = aabbMin + vec3(0.0, 0.0, diff.z / 2.0);
vec3 b = aabbMin + vec3(diff.x, 0.0, diff.z / 2.0);
vec3 c = aabbMin + vec3(diff.x / 2.0, diff.y, diff.z / 2.0);
// performing ray-triangle intersection in object space using
// Tomas Möller and Ben Trumbore:
// "Fast, Minimum Storage Ray / Triangle Intersection",
// Journal of Graphics Tools, 2(1):21--28, 1997
// here we use exactly the notation from the lecture slides
vec3 i = b - a;
vec3 j = c - a;
vec3 k = gl_ObjectRayOriginEXT - a;
vec3 r = gl_ObjectRayDirectionEXT;
// implementing ray/triangle intersection according to
// the lecture slides by computing
// (t, u, v) = (1 / (r x j) * i) ((k x i) * j, (r x j) *k, (k x i) * r)
vec3 rxj = cross(r, j);
float rxji = dot(rxj, i);
// denominator close to zero?
if (abs(rxji) < 1e-16) return;
uint hitKind = 0xFEu; // front facing
if (rxji < 0.0) {
hitKind = 0xFFu; // back facing
}
float f = 1.0f / rxji;
// compute u
float u = dot(rxj, k) * f;
if (u < 0.0f || u > 1.0f) return;
// compute v
vec3 kxi = cross(k, i);
float v = dot(kxi, r) * f;
if (v < 0.0 || v > 1.0) return;
if(u + v > 1.0) return;
// compute t
float t = dot(kxi, j) * f;
if (t < gl_RayTminEXT) return;
if (t > gl_RayTmaxEXT) return;
vec3 hitPoint = gl_ObjectRayOriginEXT + t * gl_ObjectRayDirectionEXT;
hit.texCoord = (hitPoint.xy - aabbMin.xy) / diff.xy;
hit.normal = vec3(0.0, 0.0, 1.0);
hit.baryCoord = vec2(u, v);
reportIntersectionEXT(t, hitKind);
}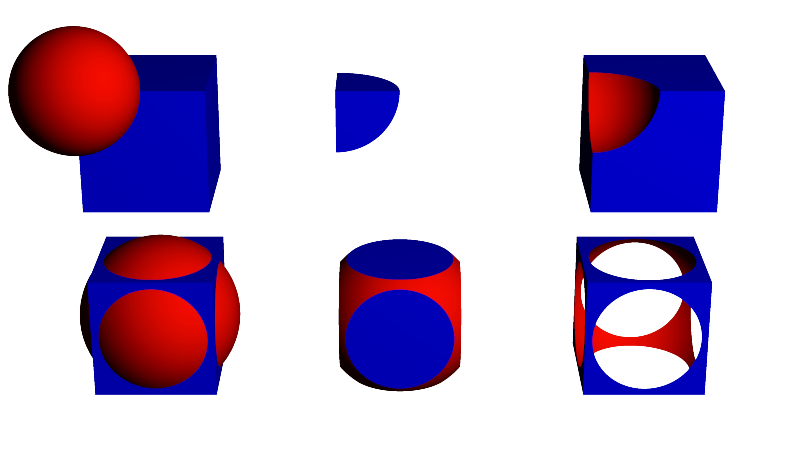

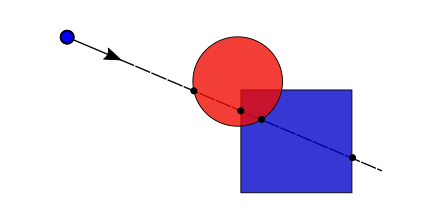

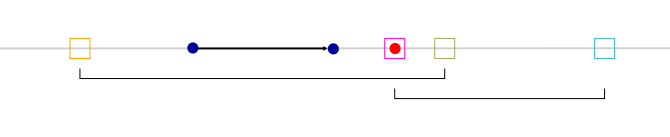
bool computeCsgUnion(in vec2 interval0, in vec2 interval1, float tmin,
out vec2 combinedInterval, out ivec2 hitIndex) {
// handle the 5 cases from the lecture/tutorial
if(interval0.x > interval0.y && interval1.x > interval1.y) {
// case 1: no intersection
combinedInterval = vec2(1e8, -1e8);
return false;
} else if(interval0.x <= interval0.y && interval1.x > interval1.y) {
// case 2: only object0
hitIndex = ivec2(0, 0); // hit object0
combinedInterval = interval0;
} else if(interval0.x > interval0.y && interval1.x <= interval1.y) {
// case 3: only object1
hitIndex = ivec2(1, 1); // hit object1
combinedInterval = interval1;
} else if(!intervalsOverlap(interval0, interval1)) {
//case 4: intervals are not overlaping
if(interval0.x < interval1.x && interval0.y >= tmin) {
combinedInterval = interval0;
hitIndex = ivec2(0, 0); // hit object0
} else if(interval1.y >= tmin) {
combinedInterval = interval1;
hitIndex = ivec2(1, 1); // hit object1
} else {
combinedInterval = vec2(1e8, -1e8);
return false;
}
} else {
//case 5: intervals are overlaping
if(interval0.x < interval1.x) {
hitIndex.x = 0; // hit object0
combinedInterval.x = interval0.x;
} else {
hitIndex.x = 1; // hit object1
combinedInterval.x = interval1.x;
}
if(interval0.y > interval1.y) {
hitIndex.y = 0; // hit object0
combinedInterval.y = interval0.y;
} else {
hitIndex.y = 1; // hit object1
combinedInterval.y = interval1.y;
}
}
return true;
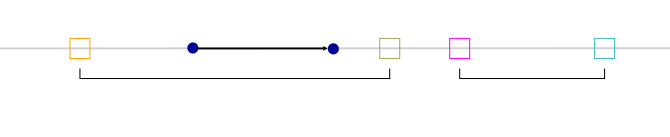
}bool computeCsgIntersection(in vec2 interval0, in vec2 interval1, float tmin,
out vec2 combinedInterval, out ivec2 hitIndex) {
// handle the 5 cases from the lecture/tutorial
if(interval0.x > interval0.y && interval1.x > interval1.y) {
// case 1: no intersection
combinedInterval = vec2(1e8, -1e8);
return false;
} else if(interval0.x <= interval0.y && interval1.x > interval1.y) {
// case 2: only object0
combinedInterval = vec2(1e8, -1e8);
return false;
} else if(interval0.x > interval0.y && interval1.x <= interval1.y) {
// case 3: only object1
combinedInterval = vec2(1e8, -1e8);
return false;
} else if(!intervalsOverlap(interval0, interval1)) {
//case 4: intervals are not overlaping
combinedInterval = vec2(1e8, -1e8);
return false;
} else {
//case 5: intervals are overlaping
if(interval0.x >= interval1.x) {
hitIndex.x = 0; // hit object0
combinedInterval.x = interval0.x;
} else {
hitIndex.x = 1; // hit object1
combinedInterval.x = interval1.x;
}
if(interval0.y <= interval1.y) {
hitIndex.y = 0; // hit object0
combinedInterval.y = interval0.y;
} else {
hitIndex.y = 1; // hit object1
combinedInterval.y = interval1.y;
}
}
return true;
}bool computeCsgDifference(in vec2 interval0, in vec2 interval1, float tmin,
out vec2 combinedInterval, out ivec2 hitIndex) {
// handle the 5 cases from the lecture/tutorial
if(interval0.x > interval0.y && interval1.x > interval1.y) {
// case 1: no intersection
combinedInterval = vec2(1e8, -1e8);
return false;
} else if(interval0.x <= interval0.y && interval1.x > interval1.y) {
// case 2: only object0
hitIndex = ivec2(0, 0); // hit object0
combinedInterval = interval0;
} else if(interval0.x > interval0.y && interval1.x <= interval1.y) {
// case 3: only object1
combinedInterval = vec2(1e8, -1e8);
return false;
} else if(!intervalsOverlap(interval0, interval1)) {
//case 4: intervals are not overlaping
combinedInterval = interval0;
hitIndex = ivec2(0, 0); // hit object0
} else {
//case 5: intervals are overlaping
if(interval0.x < interval1.x && interval1.x >= tmin) {
hitIndex = ivec2(0, 1); // first hit object0, second hit object1
combinedInterval.x = interval0.x;
combinedInterval.y = interval1.x;
} else if(interval1.y < interval0.y && interval0.y >= tmin) {
hitIndex = ivec2(1, 0); // first hit object2, second hit object0
combinedInterval.x = interval1.y;
combinedInterval.y = interval0.y;
} else {
combinedInterval = vec2(1e8, -1e8);
return false;
}
}
return true;
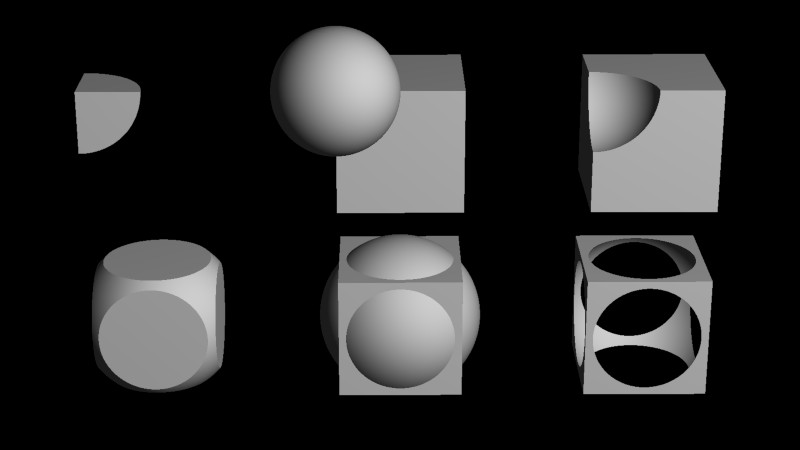
}

Please notify me by e-mail if you have questions, suggestions for improvement, or found typos: Contact