Control Keys

→ move to next slide (also Enter or Spacebar).
← move to previous slide.
 d  enable/disable drawing on slides
 p  toggles between print and presentation view
CTRL  +  zoom in
CTRL  -  zoom out
CTRL  0  reset zoom

Slides can also be advanced by clicking on the left or right border of the slide.

Notation

Type Font Examples
Variables (scalars) italics $a, b, x, y$
Functions upright $\mathrm{f}, \mathrm{g}(x), \mathrm{max}(x)$
Vectors bold, elements row-wise $\mathbf{a}, \mathbf{b}= \begin{pmatrix}x\\y\end{pmatrix} = (x, y)^\top,$ $\mathbf{B}=(x, y, z)^\top$
Matrices Typewriter $\mathtt{A}, \mathtt{B}= \begin{bmatrix}a & b\\c & d\end{bmatrix}$
Sets calligraphic $\mathcal{A}, B=\{a, b\}, b \in \mathcal{B}$
Number systems, Coordinate spaces double-struck $\mathbb{N}, \mathbb{Z}, \mathbb{R}^2, \mathbb{R}^3$

Light

  • Light is a quantized, electromagnetic wave
  • The visible range is between 380 and 770nm
  • The color of visible light corresponds to its wavelength
  • Light sources often emit a wide spectrum. Due to the superposition of many frequencies, the light appears white (e.g., daylight)
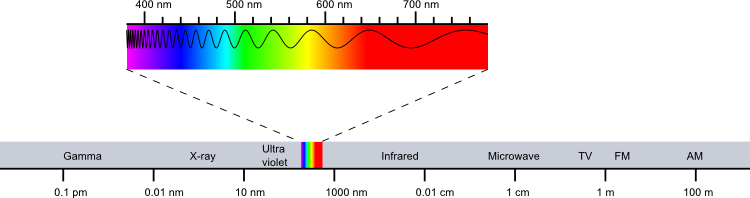
light_wavelength

Light

  • Light sources often emit a wide spectrum of different wavelengths
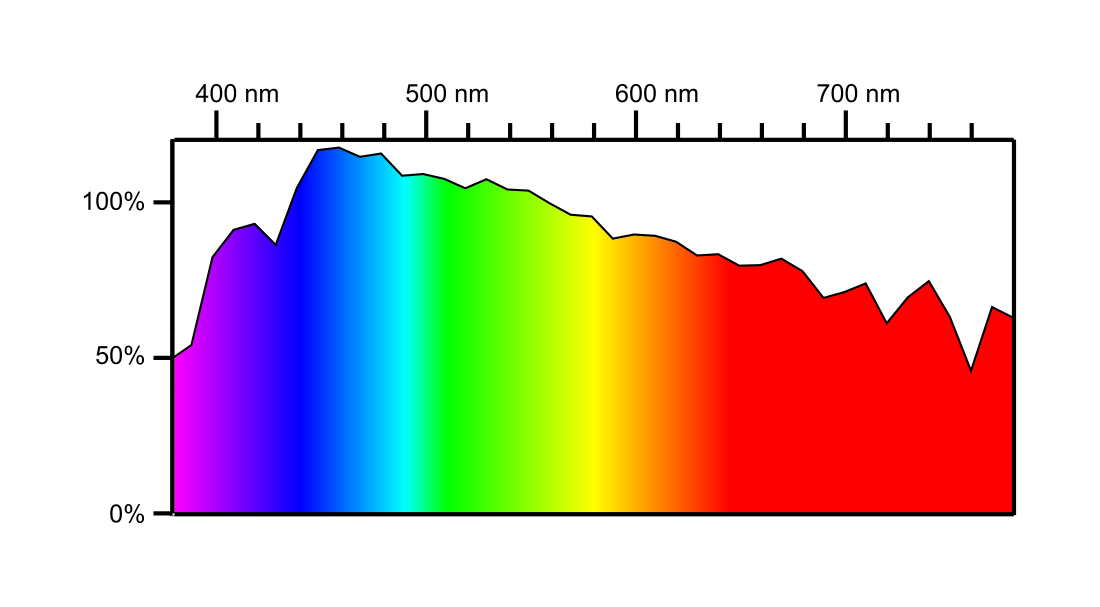
  • White light is the superposition of many wavelengths (e.g., daylight)
daylight
Spectral Power Distribution of Daylight (CIE illuminant D65)
Wavelength $\lambda$
Rel.  Spectral  Power
Data source for figure: CIE D65 Reference Spectrum,

Light Transport

lightpaths
  • Light is emitted from a light source
  • Some rays of light may hit the eye directly; others are reflected from an object's surface towards the eye
  • When it is reflected on the object surface, part of the light is typically absorbed, i.e. the light changes its color
  • If the light rays hit the eye, receptors on the retina are activated and an image is formed in the brain

Color Perception: Trichromatic Theory

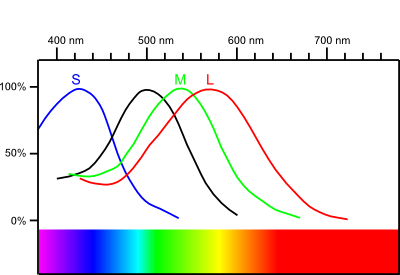
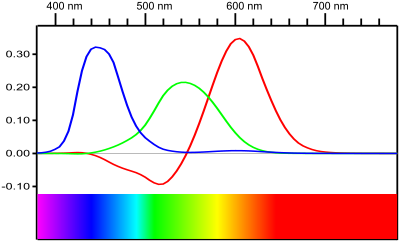
There are two systems of light sensory cells in humans:

  • System 1: rods that only react to light/dark contrasts
  • System 2: Three types of color receptors
    • L-cones
      wavelength_human_eye
      Wavelength $\lambda$
      Normalized absorption
    • M-cones
    • S-cones
Data source for figure: J. K. Bowmaker, H. J. A. Dartnall: Visual pigments of rods and cones in a human retina., The Journal of Physiology, Volume 298, Issue 1, Jan. 1980

RGB Color Space

rgb_add rgb_interp
  • Additive mixture of three primary colors (red, green, blue)
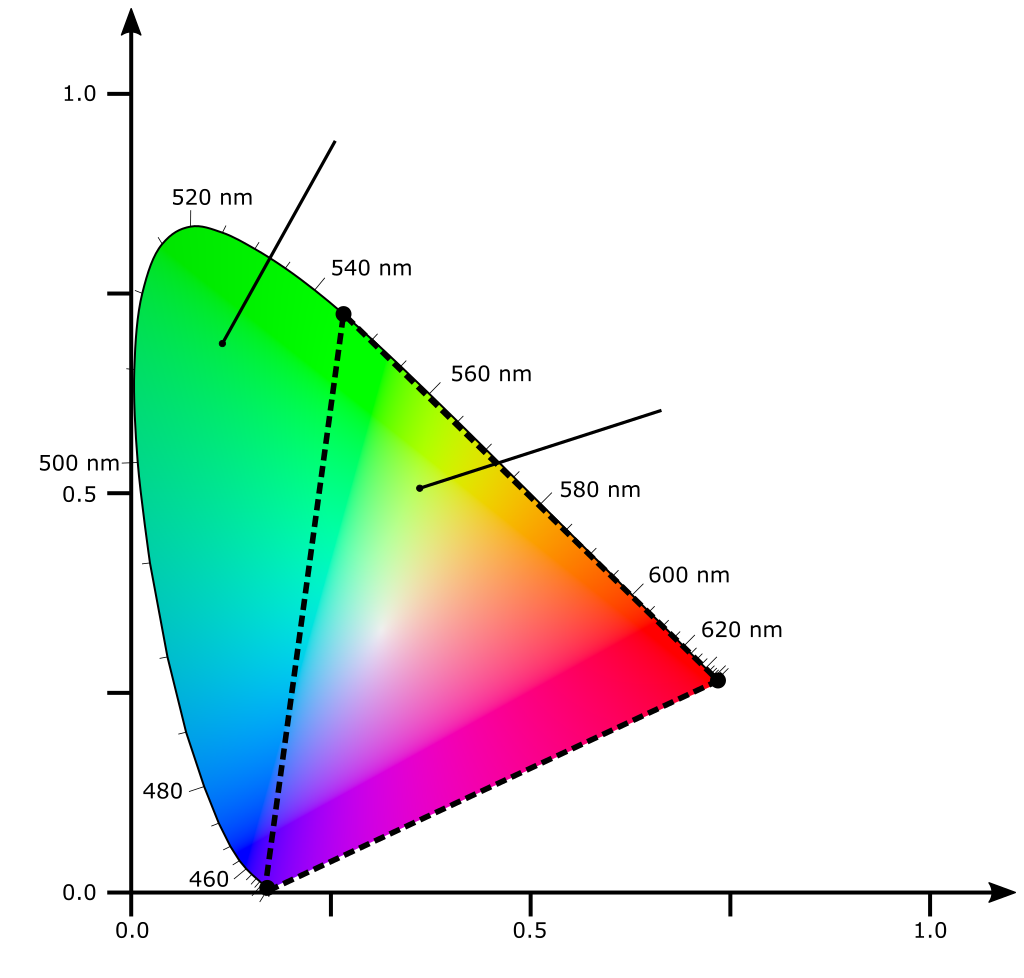
(red, green, blue) Farbe
(1.0, 0.0, 0.0)
(0.0, 1.0, 0.0)
(0.0, 0.0, 1.0)
(1.0, 1.0, 0.0)
(1.0, 0.0, 1.0)
(0.0, 1.0, 1.0)
(0.0, 0.0, 0.0)
(0.5, 0.5, 0.5)
(1.0, 1.0, 1.0)
(0.2, 0.4, 0.0)
(0.8, 0.2, 0.3)

CIE RGB Color Space

CIE_1931_chromaticity_diagram_CIERGB
all perceivable colors
CIE RGB with
positive $R$, $G$, $B$
$x$
$y$

  • Color space developed by the CIE in 1931 based on tests with human participants
  • Three lights: 700 nm (red), 546.1 nm (green), 435.8 nm (blue)
  • Question: Can all perceptible colors be mixed from these three primary colors?
  • Result: Yes, but not all coefficients are positive
CIE1931_RGBCMF
$\bar{r}(\lambda)$
$\bar{g}(\lambda)$
$\bar{b}(\lambda)$
  • Any spectral power distribution $S(\lambda)$ can be represented as follows:
    ${\small R = \int\limits_0^\infty S(\lambda) \,\bar{r}(\lambda) \,d\lambda \quad\quad G = \int\limits_0^\infty S(\lambda) \,\bar{g}(\lambda) \,d\lambda \quad\quad B = \int\limits_0^\infty S(\lambda) \,\bar{b}(\lambda) \,d\lambda \quad\quad }$

sRGB Color Space

CIE_1931_chromaticity_diagram_sRGB
  • The current standard for monitors, websites, images without an explicit color profile
  • RGB values ​​are in the range [0.0, 1.0]
  • The range of displayable colors is smaller than with CIE RGB
  • Linear transformation to CIE RGB if gamma correction is performed beforehand

sRGB Gamma

sRGB_gamma
sRGB Gamma
2.2 Gamma
  • Digital images often only use 8-bit (256 values) per color channel
  • Because the human visual system is better at distinguishing darker intensities than lighter ones, the non-linear gamma function aims to reduce the perceived quantization error (rounding error)
  • sRGB values ​​are approximately linear in perception but not linear in measured radiometric values
  • The function to decode a color channel $C$ from sRGB to the radiometric linear color space is:
    ${\small C_\mathrm{linear}= \begin{cases}\dfrac{C_\mathrm{srgb}}{12.92}, & C_\mathrm{srgb}\le0.04045 \\[5mu] \left(\dfrac{C_\mathrm{srgb}+0.055}{1.055}\right)^{\!2.4}, & C_\mathrm{srgb}>0.04045 \end{cases}}$

More Color Spaces

Mapping of CIE XYZ color space to CIE chromaticity diagram

Rendering Equation Fundamentals: Solid Angle

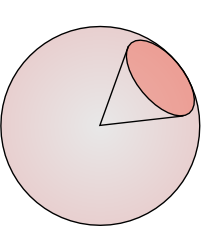
steradian
$r$
$r^2$
$\Omega=1\,\mathrm{sr}$
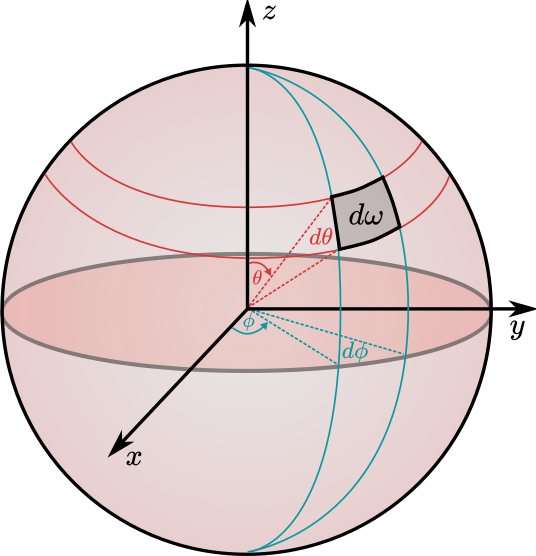
solidangle
  • The solid angle $\Omega$ of an arbitrary area $A$ corresponds to the quotient of the area $S$, which results when $A$ is projected onto a sphere of radius $r$, and $r^2$:

    $\Omega = \int\limits_{\omega}d\omega = \frac{S}{r^2}$

  • Although the solid angle is a dimensionless quantity, it is specified in the unit "steradian" $\mathrm{sr}$
  • The solid angle of a surface of constant size decreases quadratically with the distance from the center of the sphere
  • Example: A solid angle of $\Omega=1\,\mathrm{sr}$ encloses ​​on a sphere with radius $1\,\mathrm{m}$ an area of $1\,\mathrm{m}^2$. The same area located at twice the radius results in $\Omega=\frac{1}{4}\,\mathrm{sr}$
  • The following relationship exists between the differential solid angle $d\omega$ and the spherical coordinates $\theta$ and $\phi$:

    $\Omega = \int\limits_{\omega}d\omega = \int\limits_{\omega}d\theta(\sin \theta \, d\phi)= \int\limits_{\omega}\sin \theta \, d\theta \, d\phi$

Rendering Equation Fundamentals: Radiant Flux

luminous_flux
  • Radiant flux $\Phi$
  • Radiant flux = Radiant energy per time

    $\Phi = \frac{dQ}{dt} \approx \frac{\Delta Q}{\Delta t}$

  • Simplified view:
    • Every photon has the energy $E_{\small\mathrm{photon}}=\frac{h \, c}{\lambda}$ with
      $h$: Planck constant
      $c$: Speed ​​of light
      $\lambda$: Wavelength
    • Radiant flux = Sum of the photon energies that are emitted per time $\Delta t$
  • Unit: Watt $[\mathrm{W}] = [\frac{\mathrm{J}}{\mathrm{s}}]$.

Rendering Equation Fundamentals: Radiant Intensity

luminous_intensity
  • Radiant intensity $I$
  • Radiant intensity = Radiant flux per solid angle
    $I = \frac{d\Phi}{d\omega} \approx \frac{\Delta \Phi}{\Delta \omega}$
  • Radiant intensity = Sum of the photon energies that are emitted per time and solid angle
  • Unit: Watt per steradian $[\frac{\mathrm{W}}{\mathrm{sr}}]$
  • Required if the light source does not radiate equally in all directions

Rendering Equation Fundamentals: Irradiance

illuminance
  • Irradiance $E$
  • Irradiance = Radiant flux per area

    $E = \frac{d\Phi}{dA} \approx \frac{\Delta \Phi}{\Delta A}$

  • The radiant flux comes from all directions within the hemisphere above the surface
  • Unit: Watt per square metre $[\frac{\mathrm{W}}{\mathrm{m}^2}]$
  • Simplified view: Sum of the photon energies that are received per time and area

Rendering Equation Fundamentals: Radiance

luminance
  • Radiance $L$
  • Radiance = Radiant flux per solid angle and visble area

    $L = \frac{d^2\Phi}{d\omega\, \cos(\theta) \,dA} \approx \frac{\Delta \Phi}{\Delta \omega\, \cos(\theta) \,\Delta A}$

  • The area viewed from direction $\theta$ appears shortened by the factor $\cos(\theta)$
  • Application:
    • Corresponds to the observed brightness/color
    • Radiant flux in the direction of the eye
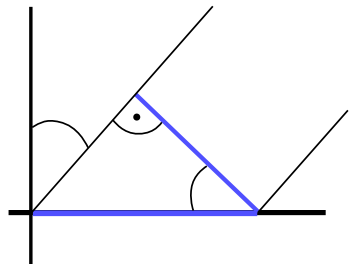
    shorter
    $\theta$
    $\theta$
    $\Delta A$
    $\cos(\theta) \,dA$
  • Simplified view: Sum of the photon energies that are emitted per time, solid angle, and visible area
  • Unit: Watt per steradian per square metre $[\frac{\mathrm{W}}{\mathrm{sr}\, \mathrm{m}^2}]$

Rendering Equation

  • The rendering equation calculates the outgoing radiance $L_o(\mathbf{v})$ for the surface point $\mathbf{x}$ with normal $\mathbf{n}$ in the direction $\mathbf{v}$ by integrating over the contributions of all incoming radiances $L_i(\mathbf{l})$ of the hemisphere above the surface

    $L_o(\mathbf{v}) = L_e(\mathbf{v}) + \int\limits_\Omega \mathrm{f}_r(\mathbf{v}, \mathbf{l})\, \, \underbrace{L_i(\mathbf{l}) \cos(\theta) \, d\omega}_{dE(\mathbf{l})}$

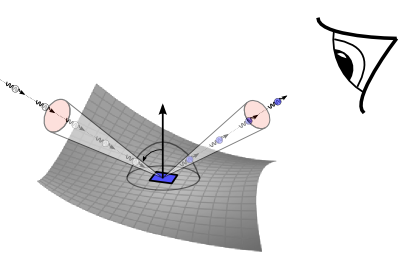
render_eqn
$\mathbf{x}$
$\theta$
$L_i(\mathbf{l})$
$L_o(\mathbf{v})$
$\Omega$
$\mathbf{n}$
  • $L_o(\mathbf{v})$ outgoing radiance
  • $L_e(\mathbf{v})$ is the radiance emitted by the surface itself
  • $L_i(\mathbf{l})$ incoming radiance
  • $E(\mathbf{l})$ irradiance
  • $\mathrm{f}_r(\mathbf{v}, \mathbf{l})$ is the so-called "Bidirectional Reflection Distribution Function" (BRDF)
  • $\Omega$ is the solid angle of the hemisphere above the surface

BRDF

BRDF (Bidirectional Reflection Distribution Function)

  • The BRDF describes the angle-dependent spectral reflection factor of a surface by the ratio of the outgoing radiance $L_o$ and the incoming irradiance $E$

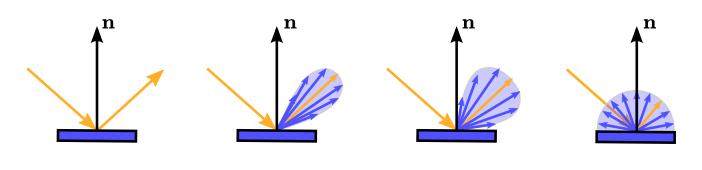
    $\mathrm{f}_r(\mathbf{v}, \mathbf{l}) = \frac{ dL_o(\mathbf{v})} { dE(\mathbf{l})} $

  • Incoming direction $\mathbf{l}$ and outgoing direction $\mathbf{v}$ can be parameterized with polar angles $\theta$ und $\phi$. Consequently, the BRDF is a 4-dimensional function.
  • By specifying this 4D function, the reflection properties of a surface are described precisely

BRDF (Bidirectional Reflection Distribution Function)

  • The "shape" of the BRDF determines the reflective properties of a surface
glossyTodiffuse
glossyTodiffuse

BRDF (Bidirectional Reflection Distribution Function)

  • The BRDF of a particular material can be measured and stored in a 4D table
  • Such tables can be found in material databases
  • 4D tables require a lot of memory and the materials cannot be edited directly
  • Therefore, for most cases, parametric BRDF models are used (Phong, Blinn-Phong, Cook-Torrance etc.)

BRDF Properties

  • Positivity:
    $\mathrm{f}_r(\mathbf{v}, \mathbf{l}) \ge 0 \quad \forall \, \mathbf{v}, \mathbf{l} \in \Omega$
  • Helmholtz reciprocity:
    $\mathrm{f}_r(\mathbf{v}, \mathbf{l}) = \mathrm{f}_r(\mathbf{l}, \mathbf{v})$
    i.e., incoming and outgoing directions can be swapped
  • Energy conservation:
    $\int\limits_\Omega \mathrm{f}_r(\mathbf{v}, \mathbf{l})\, \cos(\theta) d\omega \le 1$

Are there any questions?

questions

Please notify me by e-mail if you have questions, suggestions for improvement, or found typos: Contact

More lecture slides

Slides in German (Folien auf Deutsch)

Legal Notice, Privacy Policy,