Image Synthesis
PBR Materials
Thorsten Thormählen
June 02, 2022
Part 3, Chapter 3
Thorsten Thormählen
June 02, 2022
Part 3, Chapter 3
This is the print version of the slides.
Advance slides with the → key or
by clicking on the right border of the slide
Slides can also be advanced by clicking on the left or right border of the slide.
| Type | Font | Examples |
|---|---|---|
| Variables (scalars) | italics | $a, b, x, y$ |
| Functions | upright | $\mathrm{f}, \mathrm{g}(x), \mathrm{max}(x)$ |
| Vectors | bold, elements row-wise | $\mathbf{a}, \mathbf{b}= \begin{pmatrix}x\\y\end{pmatrix} = (x, y)^\top,$ $\mathbf{B}=(x, y, z)^\top$ |
| Matrices | Typewriter | $\mathtt{A}, \mathtt{B}= \begin{bmatrix}a & b\\c & d\end{bmatrix}$ |
| Sets | calligraphic | $\mathcal{A}, B=\{a, b\}, b \in \mathcal{B}$ |
| Number systems, Coordinate spaces | double-struck | $\mathbb{N}, \mathbb{Z}, \mathbb{R}^2, \mathbb{R}^3$ |
| Symbol | Meaning |
|---|---|
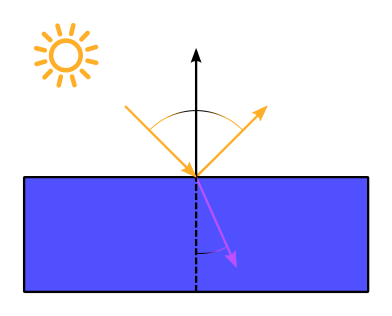
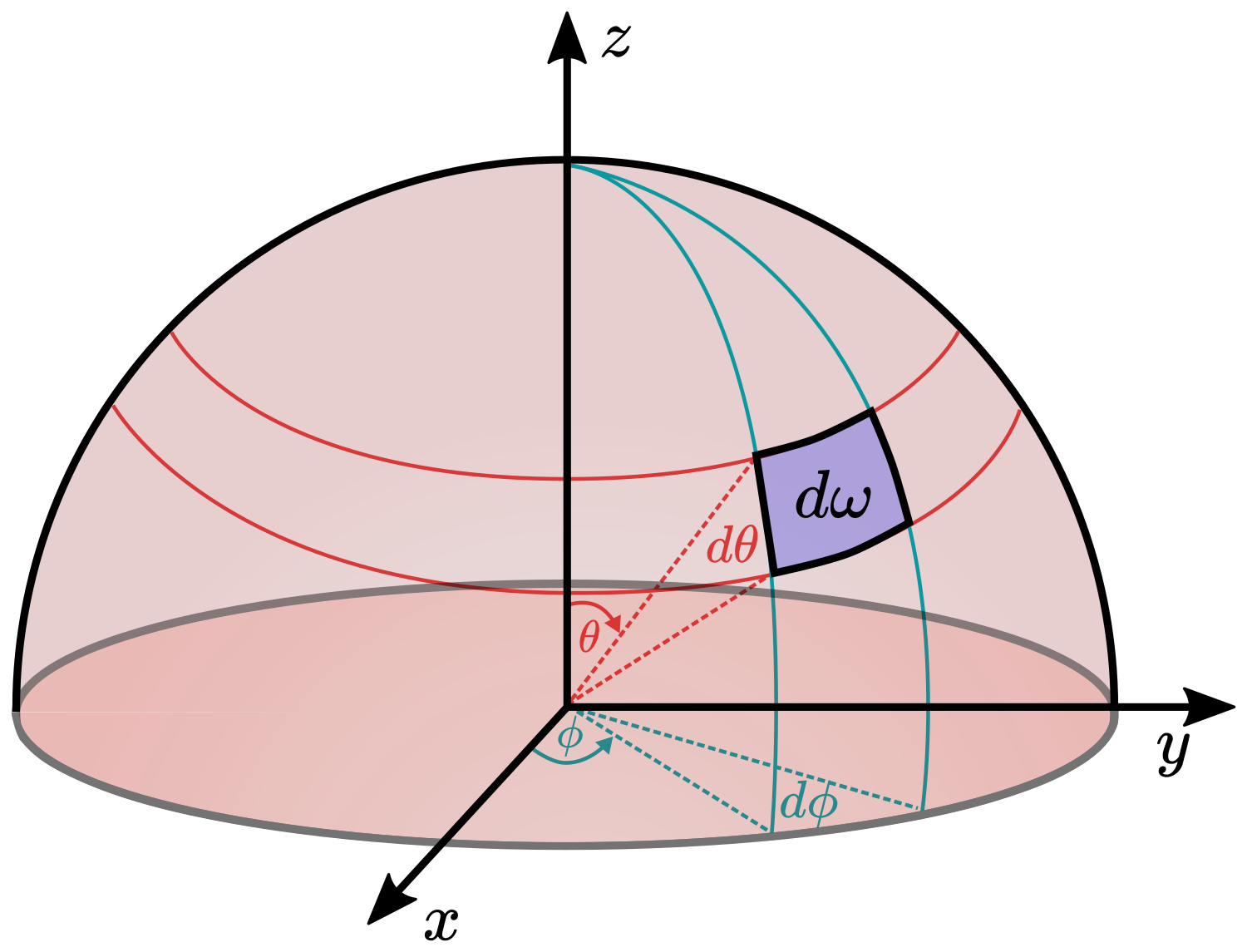
| $\Omega$ | Solid angle |
| $\theta$ | Polar angle in the spherical coordinate system |
| $\phi$ | Azimuth angle in the spherical coordinate system |
| $\Phi$ | Radiant flux |
| $I$ | Radiant intensity |
| $E$ | Irradiance |
| $L$ | Radiance |
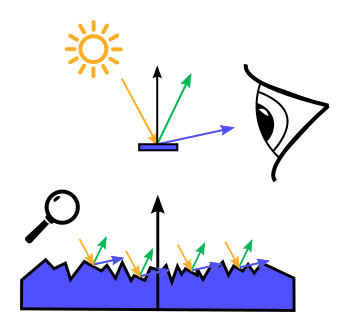
| $\mathrm{f}_r$ | BRDF (Bidirectional Reflection Distribution Function) |
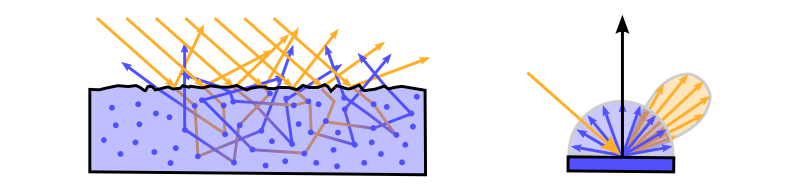
| $\mathrm{f}_d$ | Diffuse part of the BRDF |
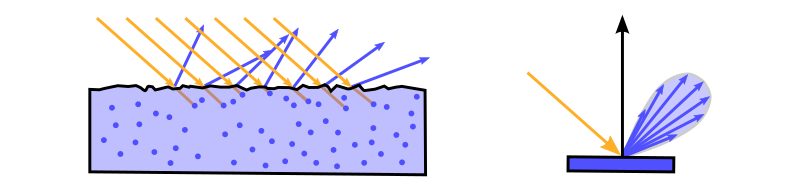
| $\mathrm{f}_s$ | Specular part of the BRDF |
| Symbol | Meaning |
|---|---|
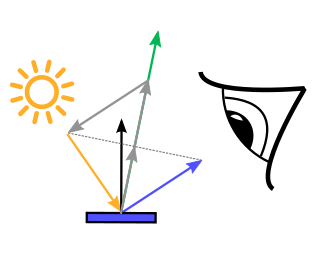
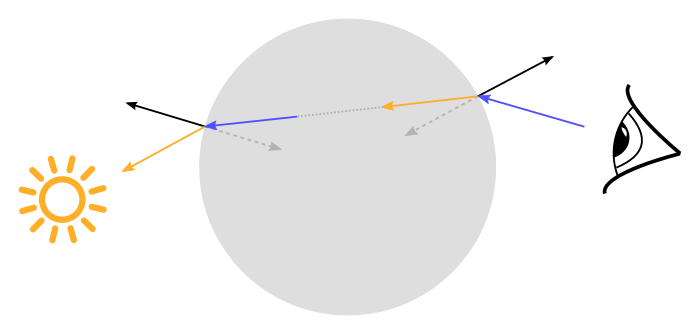
| $\mathbf{n}$ | Surface normal |
| $\mathbf{v}$ | Unit vector in view direction |
| $\mathbf{l}$ | Unit vector in light direction |
| $\eta$ | Refractive index |
| $F$ | Fresnel reflectance |
| $\mathbf{h}$ | Halfway vector between light and view direction |
| $(\dots)_+$ | Ramp function |
| $\langle \mathbf{a}\cdot \mathbf{b}\rangle$ | Scalar product |
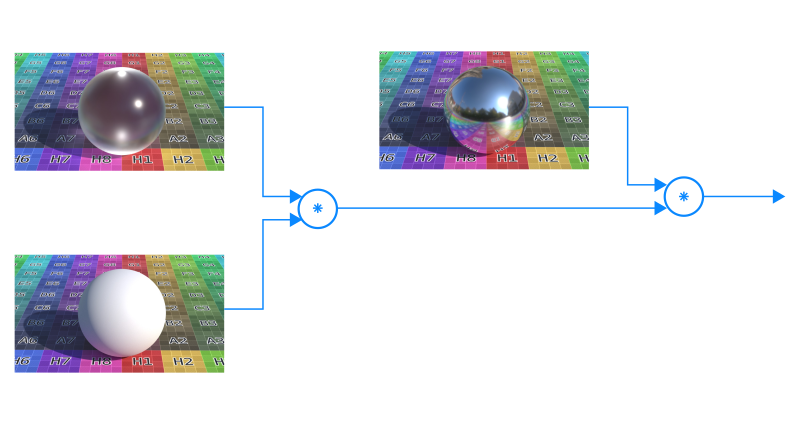

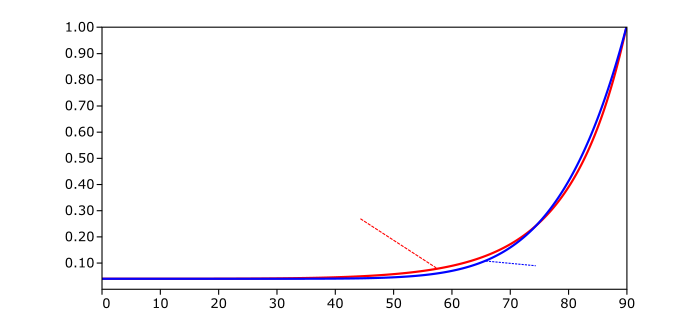
| Material | Index of Refraction | $\mathrm{F}_0$ |
|---|---|---|
| Vacuum | 1.0 | 0% |
| Air | 1.000292 | ≈ 0% |
| Water | 1.333 | 2% |
| Glass | 1.5 | 4% |
| Plastic | 1.5 to 1.58 | 4% to 5% |
| Diamond | 2.42 | 17.24% |
| Metals | $\mathrm{F}_0$ (Linear, Float) | $\mathrm{F}_0$ (sRGB, 8-bit) | Color |
|---|---|---|---|
| Titanium | (0.542, 0.497, 0.449) | (194, 187, 179) | |
| Chrome | (0.549, 0.556, 0.554) | (196, 197, 196) | |
| Iron | (0.562, 0.565, 0.578) | (198, 198, 200) | |
| Nickel | (0.660, 0.609, 0.526) | (212, 205, 192) | |
| Platinum | (0.673, 0.637, 0.585) | (214, 209, 201) | |
| Copper | (0.955, 0.638, 0.538) | (250, 209, 194) | |
| Palladium | (0.733, 0.697, 0.652) | (222, 217, 211) | |
| Zinc | (0.664, 0.824, 0.850) | (213, 234, 237) | |
| Gold | (1.022, 0.782, 0.344) | (255, 229, 158) | |
| Aluminum | (0.913, 0.922, 0.924) | (245, 246, 246) | |
| Silver | (0.972, 0.960, 0.915) | (252, 250, 245) |

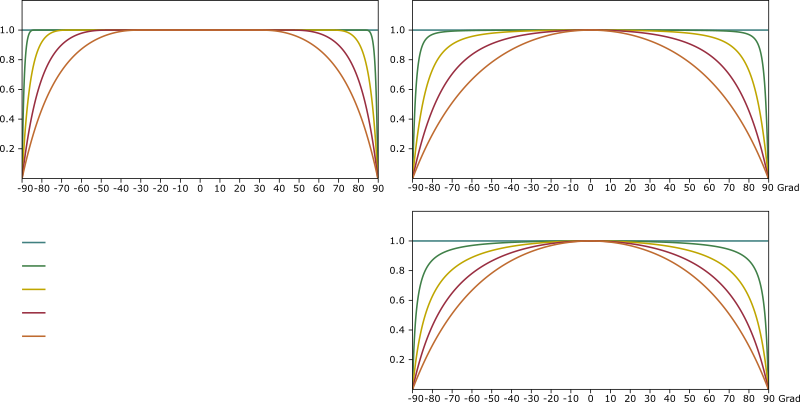
vec3 fresnelSchlick(float cosTheta, vec3 F0) {
return F0 + (1.0 - F0) * pow(1.0 - cosTheta, 5.0);
}
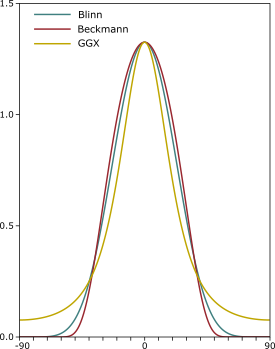
float D_GGX(float NoH, float roughness) {
float alpha = roughness * roughness;
float alpha2 = alpha * alpha;
float NoH2 = NoH * NoH;
float b = (NoH2 * (alpha2 - 1.0) + 1.0);
return alpha2 / (PI * b * b);
}
float G1_GGX_Schlick(float NdotV, float roughness) {
//float r = roughness; // original
float r = 0.5 + 0.5 * roughness; // Disney remapping
float k = (r * r) / 2.0;
float denom = NdotV * (1.0 - k) + k;
return NdotV / denom;
}
float G_Smith(float NoV, float NoL, float roughness) {
float g1_l = G1_GGX_Schlick(NoL, roughness);
float g1_v = G1_GGX_Schlick(NoV, roughness);
return g1_l * g1_v;
}
vec3 microfacetBRDF(in vec3 L, in vec3 V, in vec3 N,
in vec3 baseColor, in float metallicness,
in float fresnelReflect, in float roughness) {
vec3 H = normalize(V + L); // half vector
// all required dot products
float NoV = clamp(dot(N, V), 0.0, 1.0);
float NoL = clamp(dot(N, L), 0.0, 1.0);
float NoH = clamp(dot(N, H), 0.0, 1.0);
float VoH = clamp(dot(V, H), 0.0, 1.0);
// F0 for dielectics in range [0.0, 0.16]
// default FO is (0.16 * 0.5^2) = 0.04
vec3 f0 = vec3(0.16 * (fresnelReflect * fresnelReflect));
// in case of metals, baseColor contains F0
f0 = mix(f0, baseColor, metallicness);
// specular microfacet (cook-torrance) BRDF
vec3 F = fresnelSchlick(VoH, f0);
float D = D_GGX(NoH, roughness);
float G = G_Smith(NoV, NoL, roughness);
vec3 spec = (D * G * F) / max(4.0 * NoV * NoL, 0.001);
// diffuse
vec3 rhoD = vec3(1.0) - F; // if not specular, use as diffuse
rhoD *= 1.0 - metallicness; // no diffuse for metals
vec3 diff = rhoD * baseColor / PI;
return diff + spec;
}
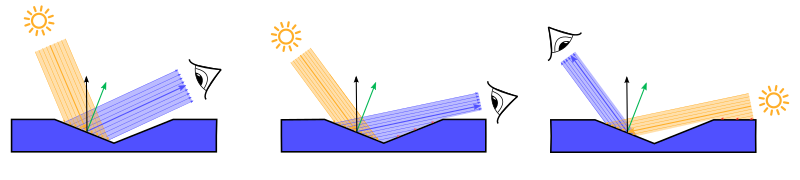
with $\theta^\ast = 2 \,\theta_h^\ast$ and $\phi^\ast = \phi_h^\ast$



Please notify me by e-mail if you have questions, suggestions for improvement, or found typos: Contact