Multimediale Signalverarbeitung
Frequenztransformationen
Thorsten Thormählen
06. Mai 2024
Teil 3, Kapitel 1
Thorsten Thormählen
06. Mai 2024
Teil 3, Kapitel 1
Dies ist die Druck-Ansicht.
Weiterschalten der Folien durch die → Taste oder
durch das Klicken auf
den rechten Folienrand.
Das Weiterschalten der Folien kann ebenfalls durch das Klicken auf den rechten bzw. linken Folienrand erfolgen.
| Typ | Schriftart | Beispiele |
|---|---|---|
| Variablen (Skalare) | kursiv | $a, b, x, y$ |
| Funktionen | aufrecht | $\mathrm{f}, \mathrm{g}(x), \mathrm{max}(x)$ |
| Vektoren | fett, Elemente zeilenweise | $\mathbf{a}, \mathbf{b}= \begin{pmatrix}x\\y\end{pmatrix} = (x, y)^\top,$ $\mathbf{B}=(x, y, z)^\top$ |
| Matrizen | Schreibmaschine | $\mathtt{A}, \mathtt{B}= \begin{bmatrix}a & b\\c & d\end{bmatrix}$ |
| Mengen | kalligrafisch | $\mathcal{A}, B=\{a, b\}, b \in \mathcal{B}$ |
| Zahlenbereiche, Koordinatenräume | doppelt gestrichen | $\mathbb{N}, \mathbb{Z}, \mathbb{R}^2, \mathbb{R}^3$ |
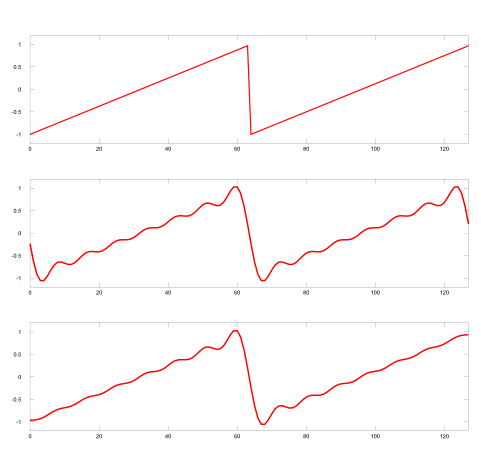
$\begin{array}{ll} \mathrm{F}[u] &= \sum\limits_{u=0}^{N-1} \mathrm{f}[n] \, e^{-2 \pi i \frac{n\, u}{N} } \\ &= \sum\limits_{u=0}^{N-1} \mathrm{f}[n]\left( \cos\left(- 2 \pi \frac{n\, u}{N} \right) + i\, \sin\left(- 2 \pi \frac{n\, u}{N} \right) \right)\\ &= \sum\limits_{u=0}^{N-1} \mathrm{f}[n]\left( \cos\left(2 \pi \frac{n\, u}{N} \right) - i\, \sin\left(2 \pi \frac{n\, u}{N} \right) \right)\\ &= \sum\limits_{u=0}^{N-1} \left(\operatorname{Re}(\mathrm{f}[n]) + i\, \operatorname{Im}(\mathrm{f}[n])\right) \left( \cos\left(2 \pi \frac{n\, u}{N} \right) - i\, \sin\left(2 \pi \frac{n\, u}{N} \right) \right) \\ \operatorname{Re}(\mathrm{F}[u]) &= \sum\limits_{u=0}^{N-1} \operatorname{Re}(\mathrm{f}[n]) \cos\left(2 \pi \frac{n\, u}{N} \right) + \operatorname{Im}(\mathrm{f}[n]) \sin\left(2 \pi \frac{n\, u}{N} \right) \\ \operatorname{Im}(\mathrm{F}[u]) &= \sum\limits_{u=0}^{N-1} \operatorname{Im}(\mathrm{f}[n]) \cos\left(2 \pi \frac{n\, u}{N} \right) - \operatorname{Re}(\mathrm{f}[n]) \sin\left(2 \pi \frac{n\, u}{N} \right) \\ \end{array} $
$\begin{array}{ll} \mathrm{f}[n] &= \frac{1}{N} \sum\limits_{u=0}^{N-1} \mathrm{F}[u] \, e^{2 \pi i \frac{n\, u}{N} } \\ &= \frac{1}{N} \sum\limits_{u=0}^{N-1} \mathrm{F}[u]\left( \cos\left(2 \pi \frac{n\, u}{N} \right) + i\, \sin\left(2 \pi \frac{n\, u}{N} \right) \right)\\ &= \frac{1}{N} \sum\limits_{u=0}^{N-1} \left(\operatorname{Re}(\mathrm{F}[u]) + i\, \operatorname{Im}(\mathrm{F}[u])\right) \left( \cos\left(2 \pi \frac{n\, u}{N} \right) + i\, \sin\left(2 \pi \frac{n\, u}{N} \right) \right) \\ \operatorname{Re}(\mathrm{f}[n]) &= \frac{1}{N} \sum\limits_{u=0}^{N-1} \operatorname{Re}(\mathrm{F}[u]) \cos\left(2 \pi \frac{n\, u}{N} \right) - \operatorname{Im}(\mathrm{F}[u]) \sin\left(2 \pi \frac{n\, u}{N} \right) \\ \operatorname{Im}(\mathrm{f}[n]) &= \frac{1}{N} \sum\limits_{u=0}^{N-1} \operatorname{Im}(\mathrm{F}[u]) \cos\left(2 \pi \frac{n\, u}{N} \right) + \operatorname{Re}(\mathrm{F}[u]) \sin\left(2 \pi \frac{n\, u}{N} \right) \\ \end{array} $
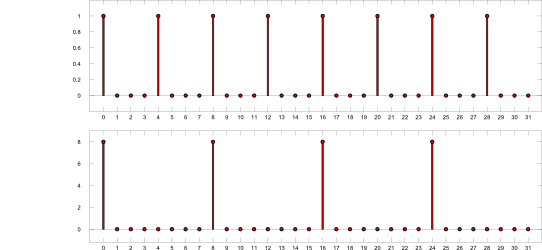
$\mathrm{f}[n] = \cos\left(2 \pi \frac{n\, u_0}{N} \right), \quad n \in [0; N-1]$
$\mathrm{F}[u] =\,\frac{N}{2} \delta(u-u_0) + \frac{N}{2} \delta(u-(N-u_0)), \quad u \in [0; N-1]$
Rechnerische Überprüfung:
$\begin{array}{ll}
\operatorname{Re}(\mathrm{f}[n]) &= \frac{1}{N} \sum\limits_{u=0}^{N-1} \operatorname{Re}(\mathrm{F}[u]) \cos\left(2 \pi \frac{n\, u}{N} \right) - \operatorname{Im}(\mathrm{F}[u]) \sin\left(2 \pi \frac{n\, u}{N} \right) \\
&= \frac{1}{N} \sum\limits_{u=0}^{N-1} \frac{N}{2} \delta(u-u_0) + \frac{N}{2} \delta(u-(N-u_0)) \cos\left(2 \pi \frac{n\, u}{N} \right) \\
&= \frac{1}{2} \cos\left(2 \pi \frac{n\, u_0}{N} \right) + \frac{1}{2} \cos\left(2 \pi \frac{n\, (N-u_0)}{N} \right) = \cos\left(2 \pi \frac{n\, u_0}{N}\right)\\
\operatorname{Im}(\mathrm{f}[n]) &= \frac{1}{N} \sum\limits_{u=0}^{N-1} \operatorname{Im}(\mathrm{F}[u]) \cos\left(2 \pi \frac{n\, u}{N} \right) + \operatorname{Re}(\mathrm{F}[u]) \sin\left(2 \pi \frac{n\, u}{N} \right) \\
&= \frac{1}{2} \sin\left(2 \pi \frac{n\, u_0}{N} \right) + \frac{1}{2} \sin\left(2 \pi \frac{n\, (N-u_0)}{N} \right) = 0\\
\end{array}
$
$\mathrm{f}[n] = \cos\left(2 \pi \frac{n\, u_0}{N} \right), \quad n \in [0; N-1]$
$\mathrm{F}[u] =\,\frac{N}{2} \delta(u-u_0) + \frac{N}{2} \delta(u-(N-u_0)), \quad u \in [0; N-1]$
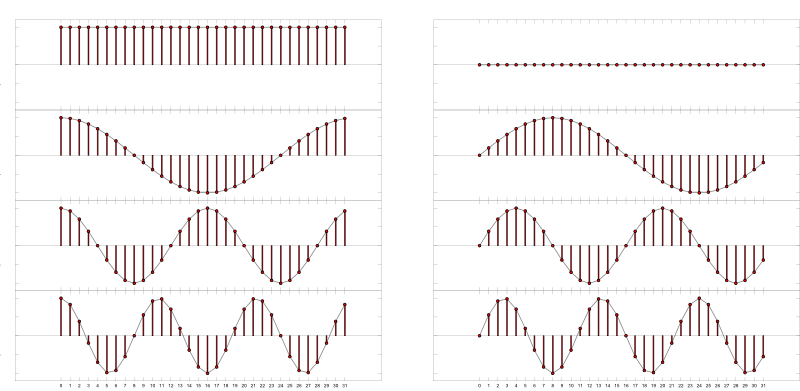
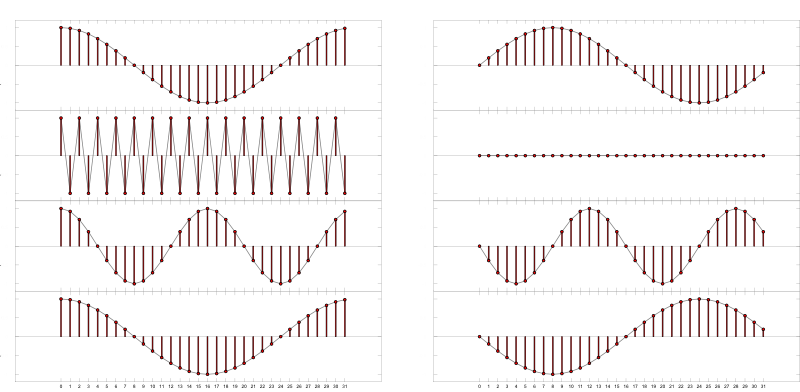
Zeichnerische Darstellung für $N =16$ und $u_0 = 3$:
$\mathrm{f}[n] = \sin\left(2 \pi \frac{n\, u_0}{N} \right), \quad n \in [0; N-1]$
$\mathrm{F}[u] =\,i \, \frac{N}{2} \left( -\delta(u-u_0) + \delta(u-(N-u_0))\right), \quad u \in [0; N-1]$
Zeichnerische Darstellung für $N =16$ und $u_0 = 3$:
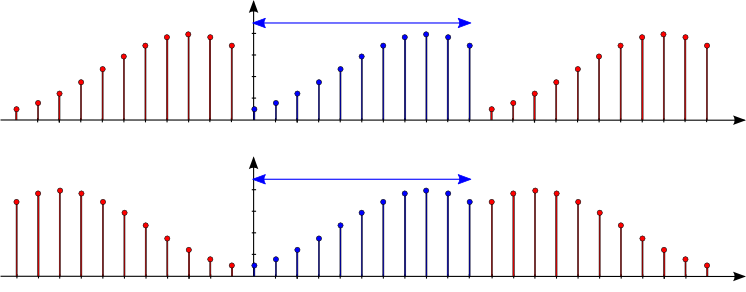
$\mathrm{f}[n] = \cos\left(2 \pi \frac{n\, u_1}{N} \right) + \sin\left(2 \pi \frac{n\, u_2}{N} \right), \quad n \in [0; N-1]$
$\mathrm{F}[u] = {\small \frac{N}{2} \delta(u-u_1) + \frac{N}{2} \delta(u-(N-u_1)) - \frac{iN}{2} \, \delta(u-u_2) + \frac{iN}{2} \delta(u-(N-u_2))}$
Zeichnerische Darstellung für $N =16$, $u_1 = 1$ und $u_2 = 3$:
$\mathrm{f}[n] = \cos\left(2 \pi \frac{n\, u_0}{N} \right) + i\,\sin\left(2 \pi \frac{n\, u_0}{N} \right), \quad n \in [0; N-1]$
$\mathrm{F}[u] =\, N \, \delta(u-u_0)$
Zeichnerische Darstellung für $N =16$ und $u_0 = 4$:
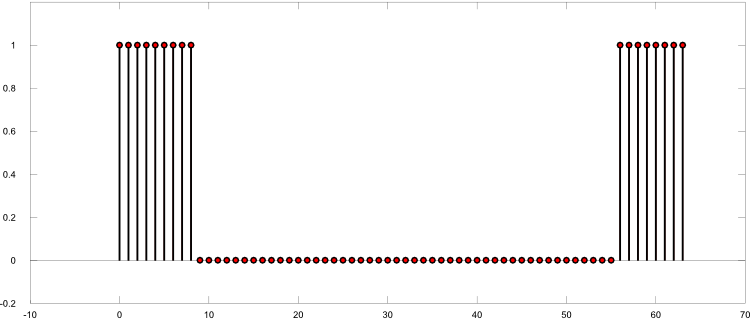
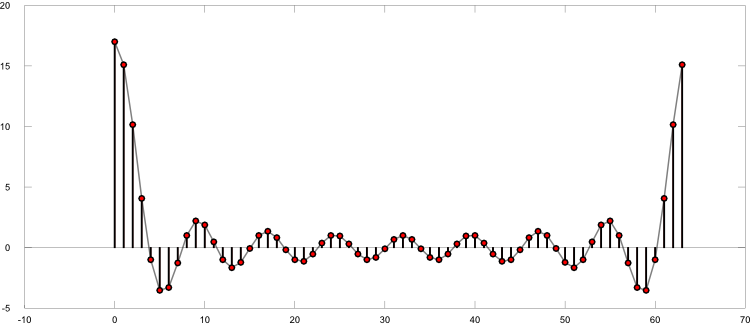
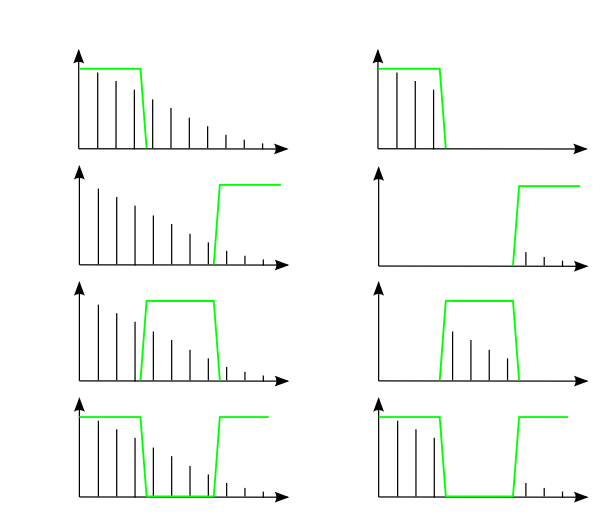
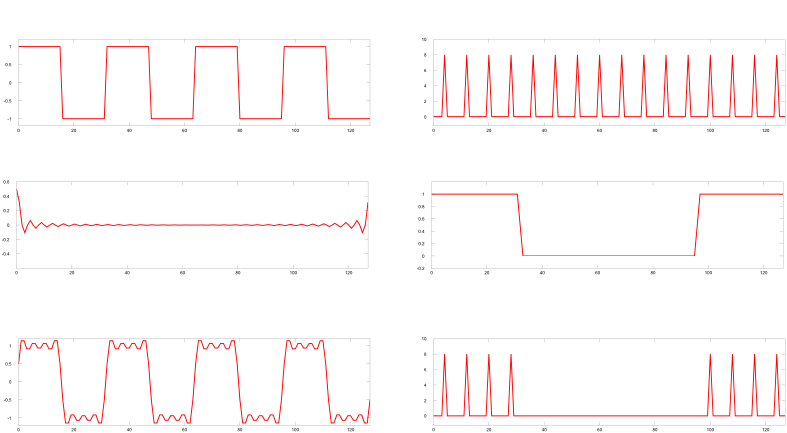

Anregungen oder Verbesserungsvorschläge können auch gerne per E-mail an mich gesendet werden: Kontakt