Control Keys

→ move to next slide (also Enter or Spacebar).
← move to previous slide.
 d  enable/disable drawing on slides
 p  toggles between print and presentation view
CTRL  +  zoom in
CTRL  -  zoom out
CTRL  0  reset zoom

Slides can also be advanced by clicking on the left or right border of the slide.

Notation

Type Font Examples
Variables (scalars) italics $a, b, x, y$
Functions upright $\mathrm{f}, \mathrm{g}(x), \mathrm{max}(x)$
Vectors bold, elements row-wise $\mathbf{a}, \mathbf{b}= \begin{pmatrix}x\\y\end{pmatrix} = (x, y)^\top,$ $\mathbf{B}=(x, y, z)^\top$
Matrices Typewriter $\mathtt{A}, \mathtt{B}= \begin{bmatrix}a & b\\c & d\end{bmatrix}$
Sets calligraphic $\mathcal{A}, B=\{a, b\}, b \in \mathcal{B}$
Number systems, Coordinate spaces double-struck $\mathbb{N}, \mathbb{Z}, \mathbb{R}^2, \mathbb{R}^3$

Light

  • Light is a quantized, electromagnetic wave
  • Speed of light in vacuum $c = 299\,792\,458 \frac{\mathrm{m}}{\mathrm{s}}$
  • The visible range is between 380 and 770 $\mathrm{nm}$
  • Visible light of a specific wavelength corresponds to a spectral color
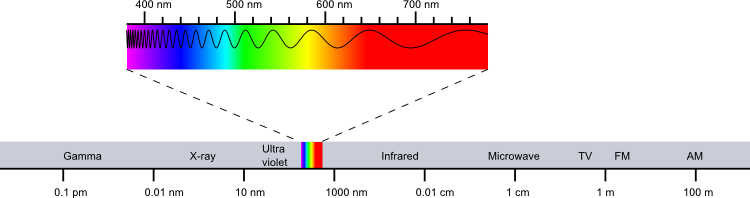
light_wavelength

Light

  • Light sources often emit a wide spectrum of different wavelengths
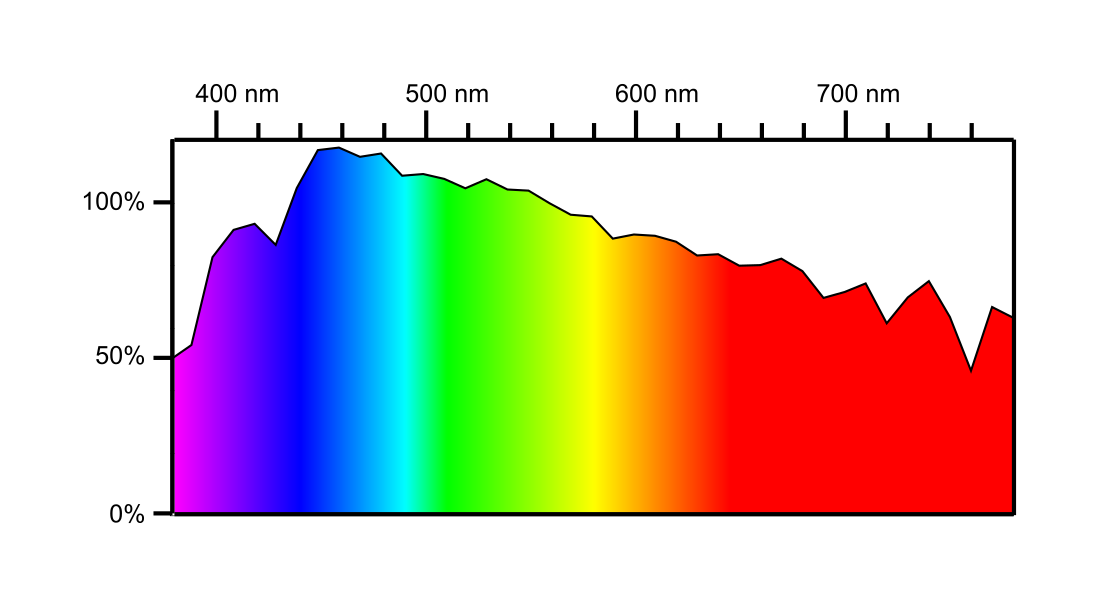
  • White light is the superposition of many wavelengths (e.g., daylight)
daylight
Spectral Power Distribution of Daylight (CIE illuminant D65)
Wavelength $\lambda$
Rel.  Spectral  Power
Data source for figure: CIE D65 Reference Spectrum,

Light Rays

lightpaths
  • Light is emitted from a light source
  • Some rays of light may hit the eye directly; others are reflected from an object's surface towards the eye
  • When it is reflected on the object surface, part of the light is typically absorbed, i.e. the light changes its color
  • If the light rays hit the eye, receptors on the retina are activated and an image is formed in the brain

Pinhole Camera

  • A pinhole camera consists of a camera body with a very small hole through which the light can enter
  • The image is formed at the back of the camera body and is displayed upside-down
  • A larger hole has the advantage that more light can enter the camera, resulting in shorter exposure times
  • The disadvantage is that multiple projections overlap and the image is out of focus
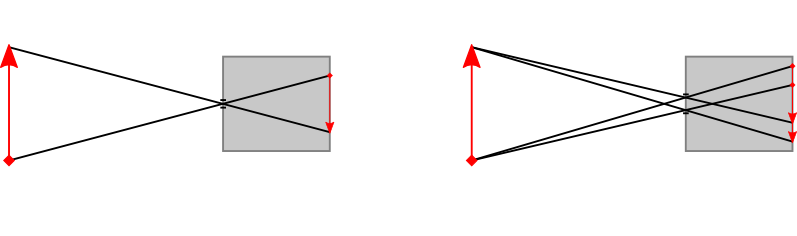
pinhole1
object
camera
pinhole
image
of the object
larger pinhole

Adding a Lens

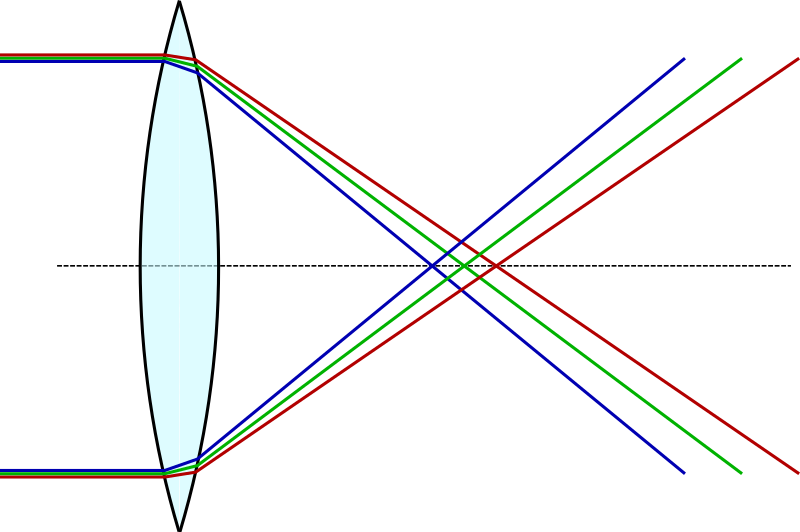
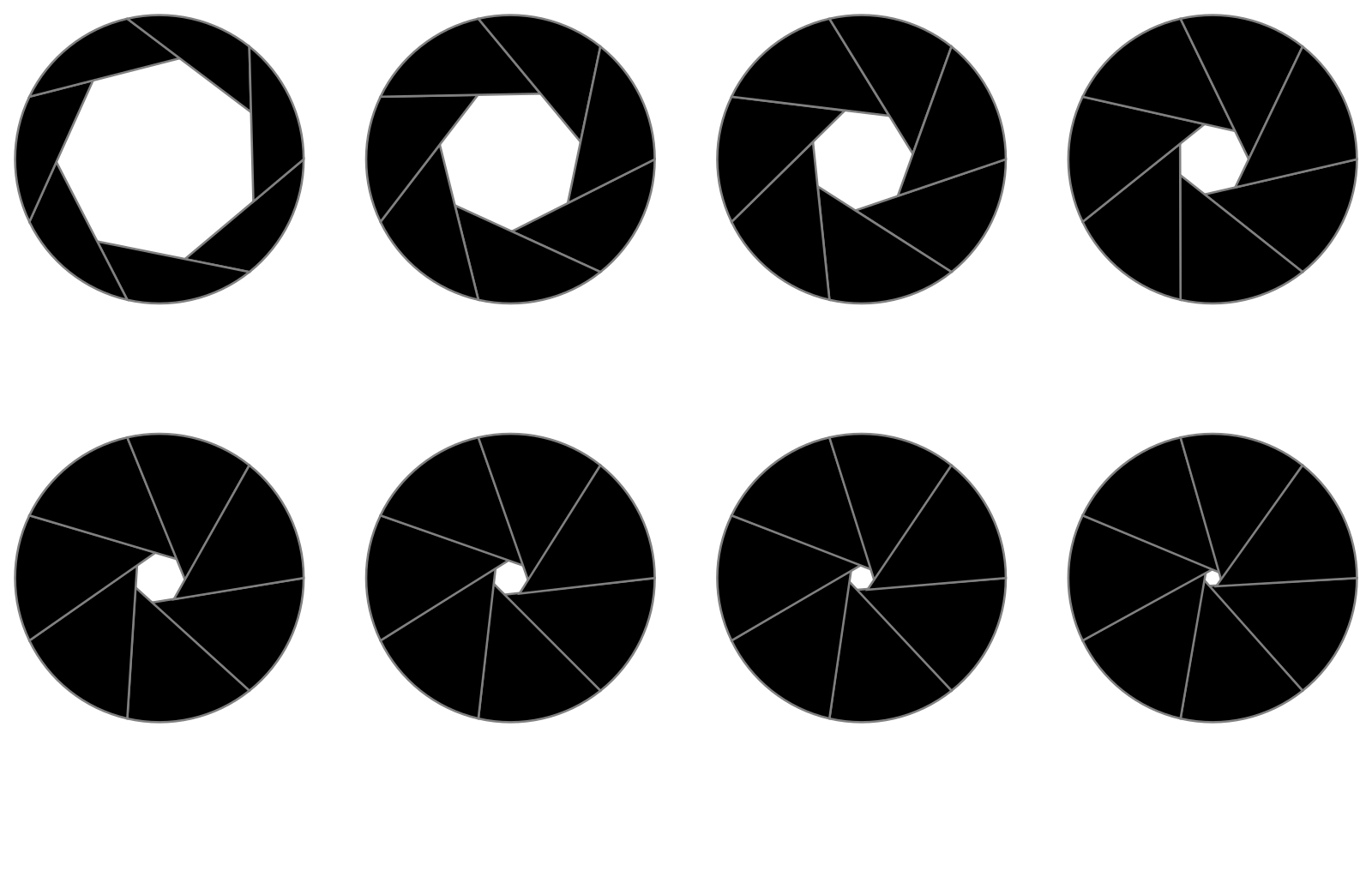
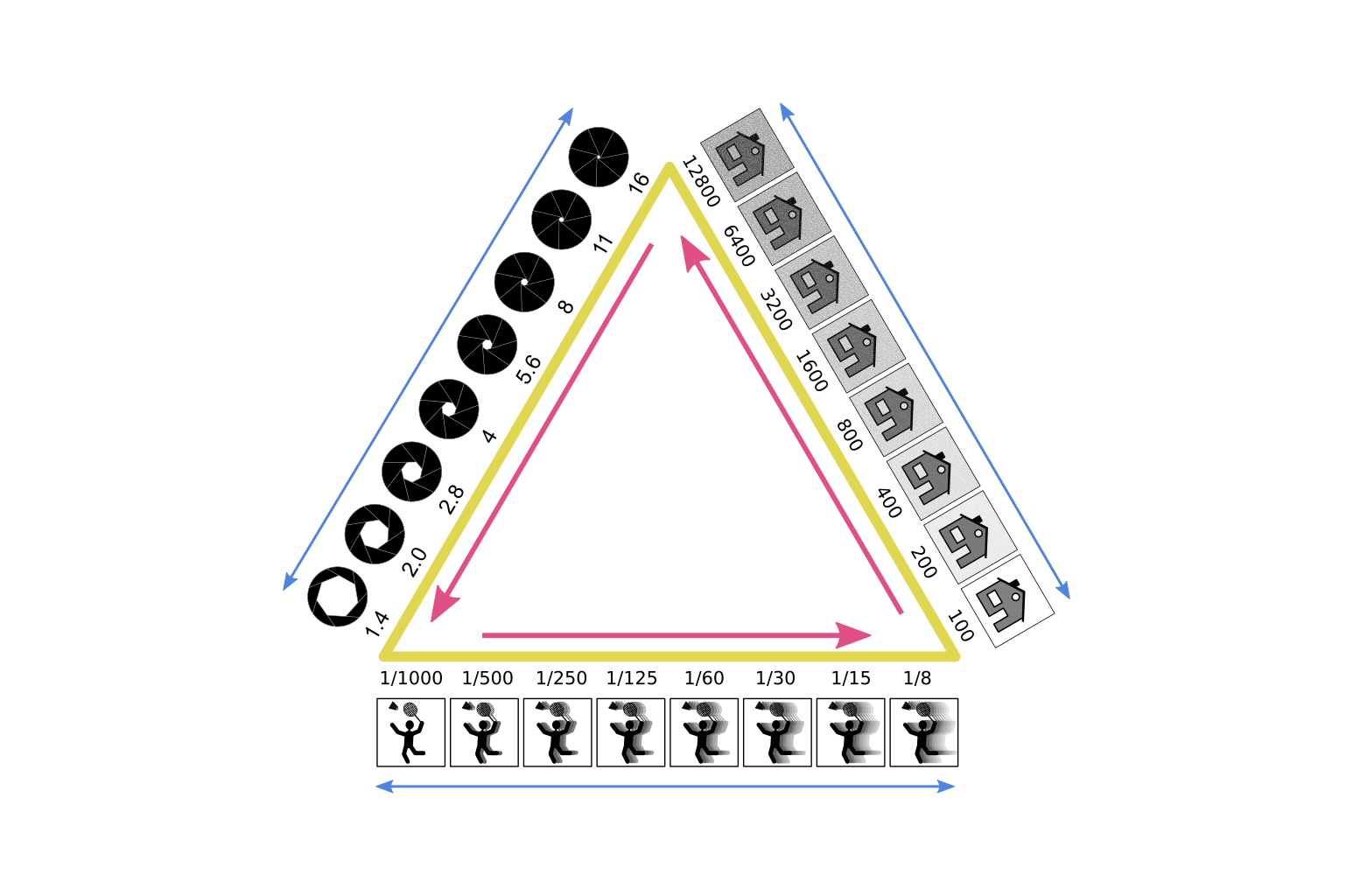
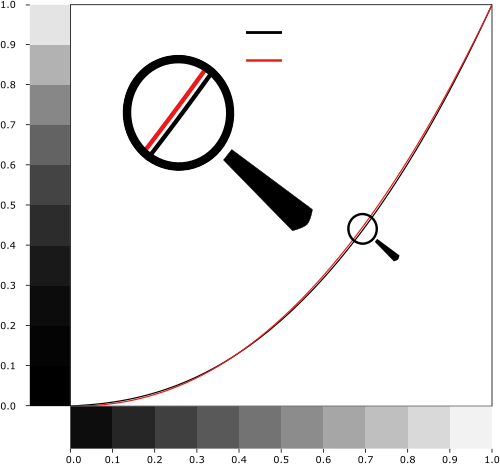
Thin lens equation: $\frac{1}{d_o} + \frac{1}{d_i} = \frac{1}{f}$       

$f$ = , $d_o$ = , $d_i$ =

Focal length $f$, object distance $d_o$, image distance $d_i$

Camera Lens

  • The purpose of the camera lens is to focus the light onto the image plane of the camera
  • However, the light can only be focused perfectly for a specific focal plane, which is parallel to the image plane in space
  • The larger the distance from the focal plane, the more blurred the result (i.e. larger circle of confusion on the image plane)
  • The main characteristic of a camera lens is its focal length $f$
    • Large focal length: telephoto lens
    • Small focal length: wide-angle lens

Camera Lens

  • With only one lens, there are problems, e.g. with chromatic aberration
  • Therefore, a camera lens typically contains a large number of lens elements to produce less errors
chromatic_aberration

Camera Lens

  • Due to the number of lens elements, their position, and shape, there are many degrees of freedom to optimize the design of a camera lens
cooke_triplet
Cooke Triplet
Double Gauss Lens
Source: based on Canon Camera Museum, EF 50mm f/1.2L USM

Aperture

  • Mechanical regulation of the incidence of light through circularly arranged blades
  • The larger the opening, the more light
  • The smaller the opening, the larger the depth of field
aperture_animation

F-Number (F-Stop)

  • The f-number $k$ is the ratio of the focal length $f$ to the diameter $D$ of the aperture
    $k = \frac{f}{D}$
  • Typical aperture series:
    $k = $   1.4     2.0     2.8     4     5.6     8     11     16     22
  • Example for a lens with a focal length of 50 mm :
    $D = \frac{50{\small \,\mbox{mm}}}{1.4} = 35.7\,\mbox{mm}$    Circular area $\pi \, r^2= \pi \, \left(\frac{35.7{\small \,\mbox{mm}}}{2}\right)^2 \approx 100\,\mbox{mm}^2$
    $D = \frac{50{\small \,\mbox{mm}}}{2.0} = 25\,\mbox{mm}$         Circular area: $\pi \, r^2= \pi \, \left(\frac{25{\small \,\mbox{mm}}}{2}\right)^2 \,\,\,\approx 50\,\mbox{mm}^2$
  • The circular area is halved with each step of the aperture series
  • The larger the f-number, the smaller the aperture
  • The larger the f-number, the larger the depth of field

F-Number (F-Stop)

aperture
1.4
2.0
2.8
4
5.6
8
11
16

Film Speed (ISO)

  • Sensitivity of the analog film
  • Analog film is made of crystals of silver halide embedded in gelatin
  • The large the crystals, the more light-sensitive is the film
  • The smaller the crystals, the higher the optical resolution
  • ISO number serves as a standard:
    • ISO 100 (for sunshine)
    • ISO 200 (for cloudy weather)
    • ISO 400 (for indoors, twilight)
  • Doubling the ISO number halves the exposure time
  • The higher the ISO number, the large the image noise
  • Digital cameras:
    • Photon noise and electronic noise
    • Digital cameras also have an ISO setting, which amplifies the signal (and the noise)
    • Larger digital sensors typically have a better signal-to-noise-ratio (SNR)

The Exposure Triangle

exposure_triangle
brighter
brighter
brighter
Exposure Time
more
motion blur
less
motion blur
ISO
less
noise
more
noise
Aperture
shallow
depth of field
deep
depth of field

Color Filter Array (CFA)

  • To capture RGB values with a single CCD or CMOS chip, the pixels of the image sensor are covered with color filters
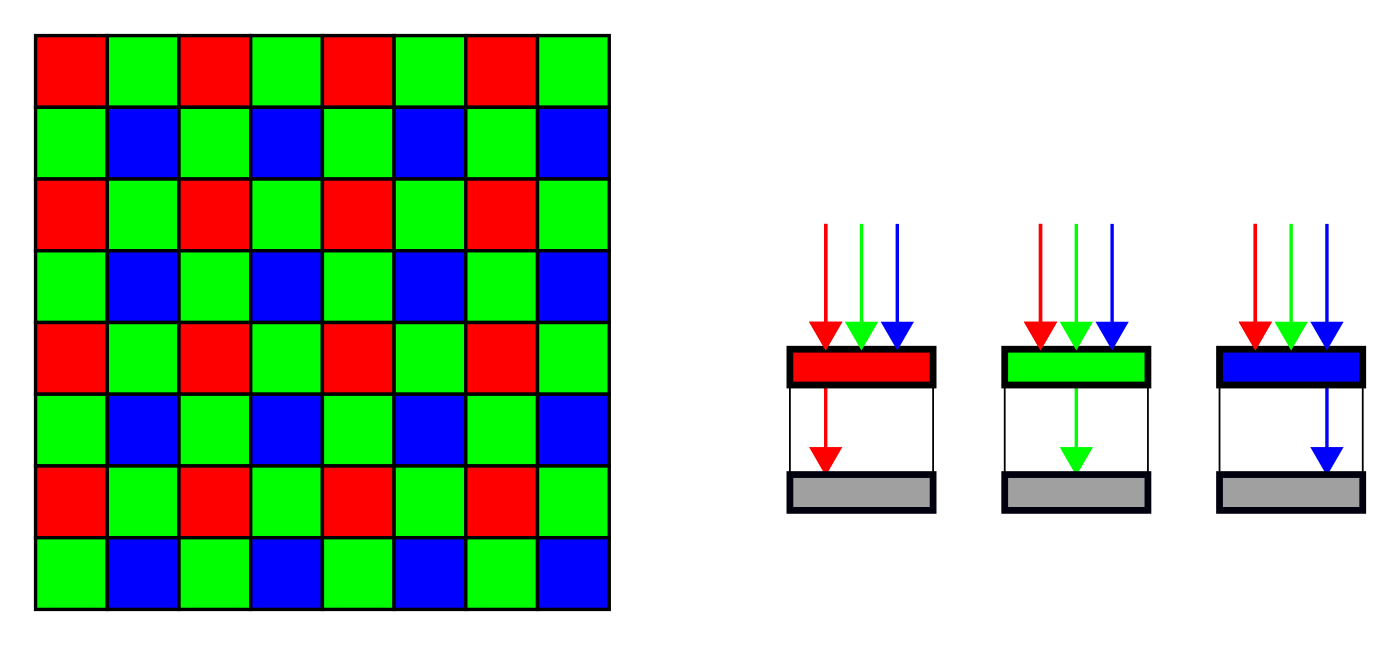
  • A popular arrangement is the Bayer pattern:
bayer_pattern

Color Perception: Trichromatic Theory

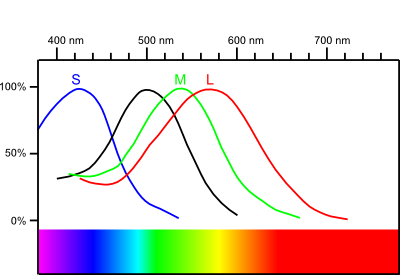
There are two systems of light sensory cells in humans:

  • System 1: rods that only react to light/dark contrasts
  • System 2: Three types of color receptors
    • L-cones
      wavelength_human_eye
      Wavelength $\lambda$
      Normalized absorption
    • M-cones
    • S-cones
Data source for figure: J. K. Bowmaker, H. J. A. Dartnall: Visual pigments of rods and cones in a human retina., The Journal of Physiology, Volume 298, Issue 1, Jan. 1980

RGB Color Space

rgb_add rgb_interp
  • Additive mixture of three primary colors (red, green, blue)
(red, green, blue) Farbe
(1.0, 0.0, 0.0)
(0.0, 1.0, 0.0)
(0.0, 0.0, 1.0)
(1.0, 1.0, 0.0)
(1.0, 0.0, 1.0)
(0.0, 1.0, 1.0)
(0.0, 0.0, 0.0)
(0.5, 0.5, 0.5)
(1.0, 1.0, 1.0)
(0.2, 0.4, 0.0)
(0.8, 0.2, 0.3)

CIE RGB Color Space

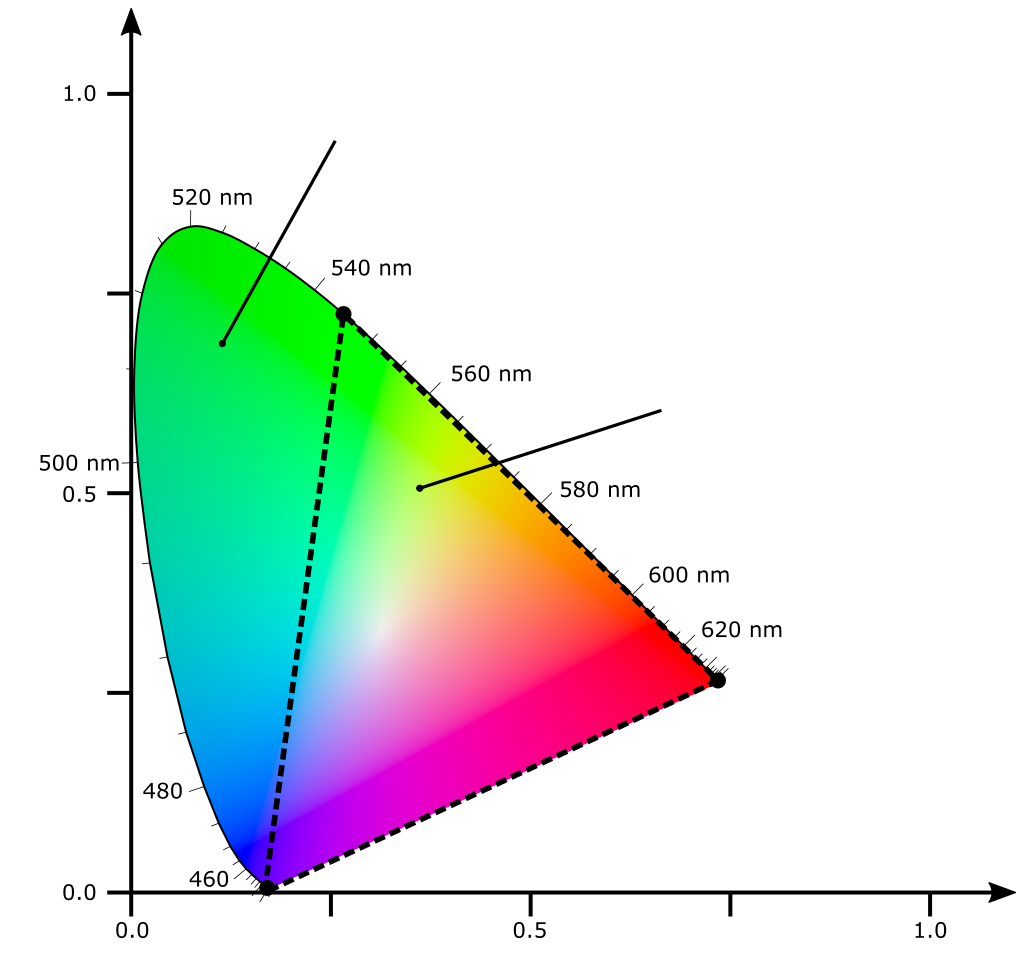
CIE_1931_chromaticity_diagram_CIERGB
all perceivable colors
CIE RGB with
positive $R$, $G$, $B$
$x$
$y$

  • Color space developed by the CIE in 1931 based on tests with human participants
  • Three lights: 700 nm (red), 546.1 nm (green), 435.8 nm (blue)
  • Question: Can all perceptible colors be mixed from these three primary colors?
  • Result: Yes, but not all coefficients are positive
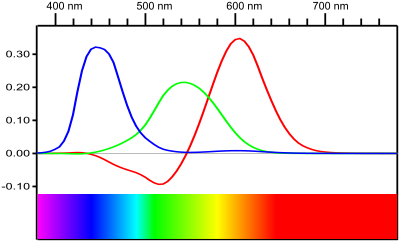
CIE1931_RGBCMF
$\bar{r}(\lambda)$
$\bar{g}(\lambda)$
$\bar{b}(\lambda)$
  • Any spectral power distribution $S(\lambda)$ can be represented as follows:
    ${\small R = \int\limits_0^\infty S(\lambda) \,\bar{r}(\lambda) \,d\lambda \quad\quad G = \int\limits_0^\infty S(\lambda) \,\bar{g}(\lambda) \,d\lambda \quad\quad B = \int\limits_0^\infty S(\lambda) \,\bar{b}(\lambda) \,d\lambda \quad\quad }$

CIE XYZ Color Space

  • Linear transformation of the CIE RGB colorspace such that all color matching functions are not in the negative range
    $\small \begin{pmatrix} X \\ Y \\ Z \end{pmatrix} = \begin{bmatrix}0.49000 & 0.31000 & 0.20000\\ 0.17697 & 0.81240 & 0.01063 \\ 0.00000 & 0.010000 & 0.99000\end{bmatrix} \begin{pmatrix} R \\ G \\ B \end{pmatrix}$
  • $Y$ parameter is a measure of the luminance
  • Constant energy white point lies at $X$ = $Y$ = $Z$ = $\frac{1}{3}$
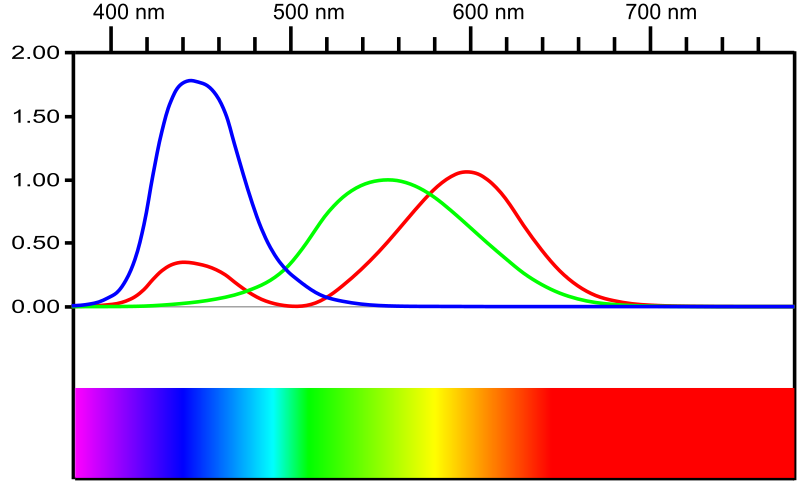
CIE1931_XYZCMF
$\bar{x}(\lambda)$
$\bar{y}(\lambda)$
$\bar{z}(\lambda)$
  • Any spectral power distribution $S(\lambda)$ can be represented as follows:
    ${\small X = \int\limits_0^\infty S(\lambda) \,\bar{x}(\lambda) \,d\lambda \quad\quad Y = \int\limits_0^\infty S(\lambda) \,\bar{y}(\lambda) \,d\lambda \quad\quad Z = \int\limits_0^\infty S(\lambda) \,\bar{z}(\lambda) \,d\lambda \quad\quad }$
Data source for figure: cie.15.2004.tables.xls

CIE xy Chromaticity Diagram

CIE_1931_chromaticity_diagram_CIERGB
all perceivable colors
CIE RGB with
positive $R$, $G$, $B$
$x$
$y$
  • Projection of the CIE XYZ values to the following xy plane
    $x = \frac{X}{X+Y+Z}$
    $y = \frac{Y}{X+Y+Z}$
  • The diagram contains the chromaticity of all perceivable colors
  • Luminance value is not relevant for position in the diagram

sRGB Color Space

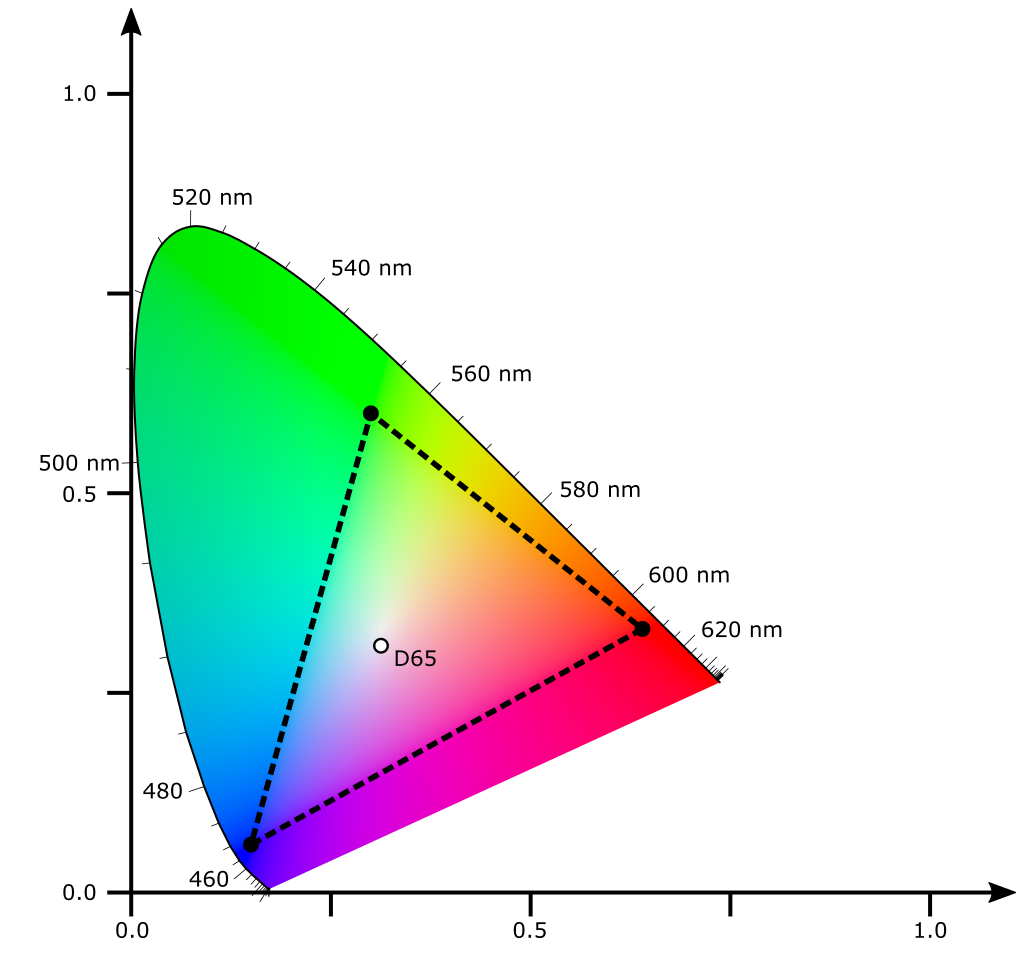
CIE_1931_chromaticity_diagram_sRGB
  • The current standard for monitors, websites, images without an explicit color profile
  • RGB values ​​are in the range [0.0, 1.0]
  • The range of displayable colors is smaller than with CIE RGB
  • Linear transformation to CIE RGB and CIE XYZ if gamma correction is performed beforehand
    $\begin{pmatrix} X \\ Y \\ Z \end{pmatrix} = \begin{bmatrix}0.4124 & 0.3576 & 0.1805\\ 0.2126 & 0.7152 & 0.0722 \\ 0.0193 & 0.1192 & 0.9505\end{bmatrix} \begin{pmatrix} R_\mathrm{linear} \\ G_\mathrm{linear} \\ B_\mathrm{linear} \end{pmatrix}$

sRGB Gamma

sRGB_gamma
sRGB Gamma
2.2 Gamma
  • Digital images often only use 8-bit (256 values) per color channel
  • Because the human visual system is better at distinguishing darker intensities than lighter ones, the non-linear gamma function aims to reduce the perceived quantization error (rounding error)
  • sRGB values ​​are approximately linear in perception but not linear in measured radiometric values
  • The function to decode a color channel $C$ from sRGB to the radiometric linear color space is:
    ${\small C_\mathrm{linear}= \begin{cases}\dfrac{C_\mathrm{srgb}}{12.92}, & C_\mathrm{srgb}\le0.04045 \\[5mu] \left(\dfrac{C_\mathrm{srgb}+0.055}{1.055}\right)^{\!2.4}, & C_\mathrm{srgb}>0.04045 \end{cases}}$

Raw to sRGB

raw_pipeline
Raw Sensor Data
Linearization
Linearization Table
Black Subtraction
Black Level
Normalization
logical 0.0 to 1.0 range
Clipping
0.0 to 1.0 range
Demosaicing
Camera Color Space to XYZ
XYZ to sRGB
sRGB

YCbCr Color Space

  • YCbCr color space is often used for digital images and video
  • ITU-R BT.709 conversion:
    $\begin{pmatrix} Y' \\ C_b \\ C_r \end{pmatrix} = \begin{bmatrix}0.2126 & 0.7152 & 0.0722\\ -0.11468 & -0.3854 & 0.5 \\ 0.5 & -0.4542 & -0.0458\end{bmatrix} \begin{pmatrix} R'\\ G'\\ B' \end{pmatrix}$
  • $Y$ is the luminance (non-linearly encoded)
  • $C_b$ and $C_r$ are the chrominance components
  • $R'$, $G'$, $B'$ are RGB values (non-linearly encoded)
game pieces    game pieces    game pieces
Input image
Luminance
Chrominance
Source: input image from Alexas_Fotos, Pixabay

YCbCr Chroma Subsampling

  • In the human visual system, the rods (for the luminance) are denser than cones (for the chrominance)
  • Therefore, to save data rate, the chrominance can be sampled with a lower sampling rate in the YCbCr colorspace
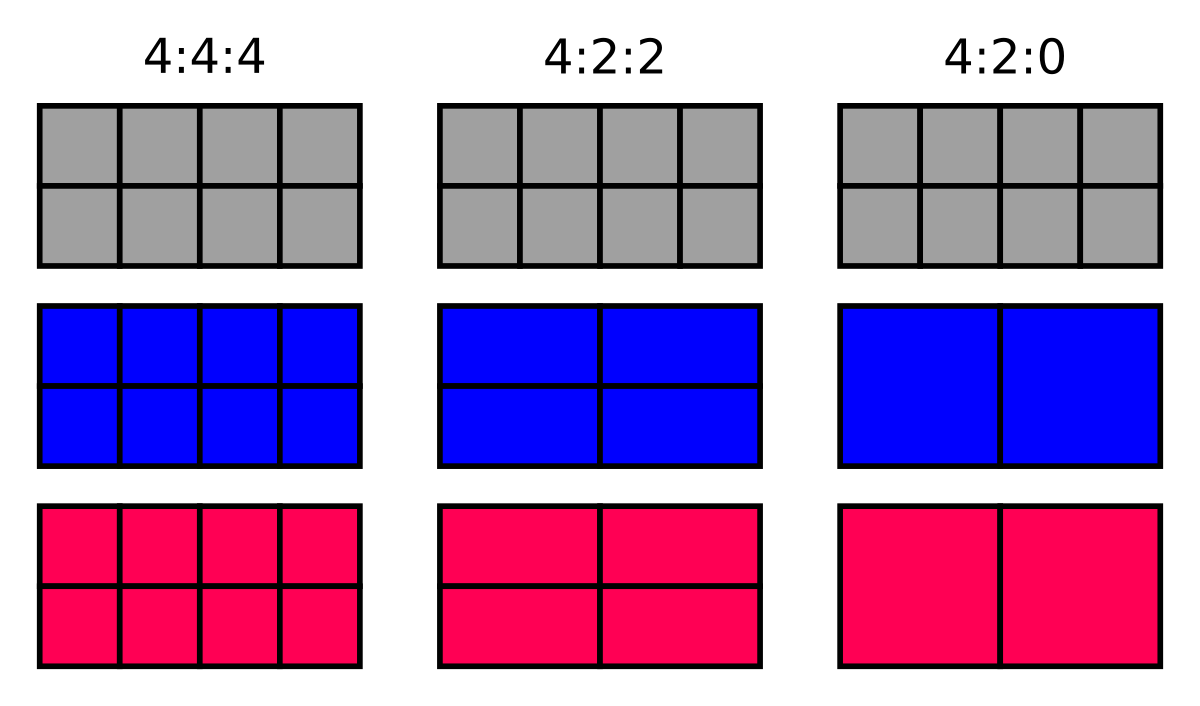
    chroma_subsampling2
    $Y$
    $C_b$
    $C_r$
  • Notation a : b : c
    • a is is the pixel width that is considered (usually 4 pixels)
    • b number of chrominance samples in the first row
    • c number of chrominance samples in the second row

Digital TV Broadcast Formats

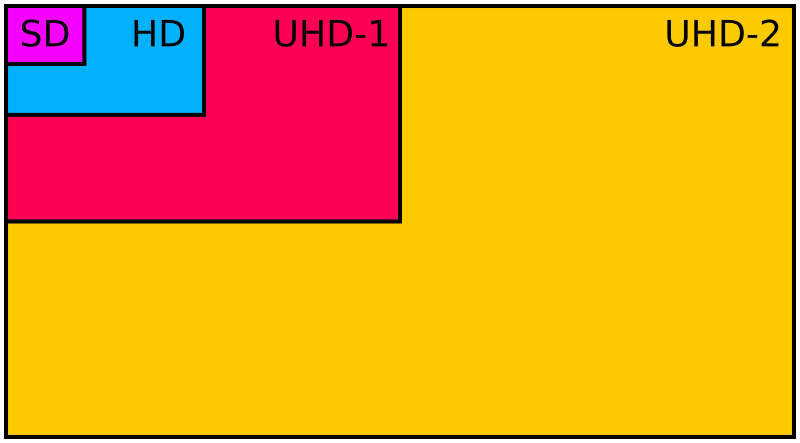
FormatSD (PAL / NTSC)HDUHD-1UHD-2
ITU-R Rec.BT.601BT.709BT.2020BT.2020
Scan lines576 / 480108021604320
Pixels per line720192038407680
Aspect ratio4:316:916:916:9
Frames per second (FPS)50i / 60i24p - 60p24p - 120p24p - 120p
tv_formats

Digital TV Broadcast Formats

  • TV broadcast formats are identified with three major parameters:
  • Examples:
    • 576i50 means 576 scan lines with an interlaced scanning format with 25 frames (50 fields) per second
    • 1080p30 means 1080 scan lines with a progressive scanning format with 30 frames per second

To be continued...

Are there any questions?

questions

Please notify me by e-mail if you have questions, suggestions for improvement, or found typos: Contact

More lecture slides

Slides in German (Folien auf Deutsch)

Legal Notice, Privacy Policy,