Control Keys

→ move to next slide (also Enter or Spacebar).
← move to previous slide.
 d  enable/disable drawing on slides
 p  toggles between print and presentation view
CTRL  +  zoom in
CTRL  -  zoom out
CTRL  0  reset zoom

Slides can also be advanced by clicking on the left or right border of the slide.

Notation

Type Font Examples
Variables (scalars) italics $a, b, x, y$
Functions upright $\mathrm{f}, \mathrm{g}(x), \mathrm{max}(x)$
Vectors bold, elements row-wise $\mathbf{a}, \mathbf{b}= \begin{pmatrix}x\\y\end{pmatrix} = (x, y)^\top,$ $\mathbf{B}=(x, y, z)^\top$
Matrices Typewriter $\mathtt{A}, \mathtt{B}= \begin{bmatrix}a & b\\c & d\end{bmatrix}$
Sets calligraphic $\mathcal{A}, B=\{a, b\}, b \in \mathcal{B}$
Number systems, Coordinate spaces double-struck $\mathbb{N}, \mathbb{Z}, \mathbb{R}^2, \mathbb{R}^3$

Contents

  • Representation of unsigned integers
  • Representation of signed integer numbers
    • Sign-magnitude representation
    • Ones' complement
    • Two's complement
  • Representation of signed rational numbers
    • Fixed-point representation
    • Floating-point representation

Representation of Unsigned Integers

  • Depending on how many bits are available to store an unsigned integer in binary, different integer ranges can be represented
BytesBitsRange of valuesName of the data type (Microsoft Visual C++)
18$[0;255]$unsigned char
216$[0;65535]$unsigned short
432$[0;4294967295]$unsigned int
864$[0;18446744073709551615]$unsigned long long
Source: Data Type Ranges, Visual Studio 2013

Big-Endian and Little-Endian Storage

  • Little-Endian
    • The byte with the lowest significance is stored first
    • All x86-compatible computers use this ordering
little endian
  • Big-Endian
    • The byte with the lowest significance is stored last
    • MIPS, SPARC, PowerPC, Java Virtual Machine, etc.
big endian

Representation of Signed Integer Numbers

  • If positive and negative numbers have to be stored, there are several options:
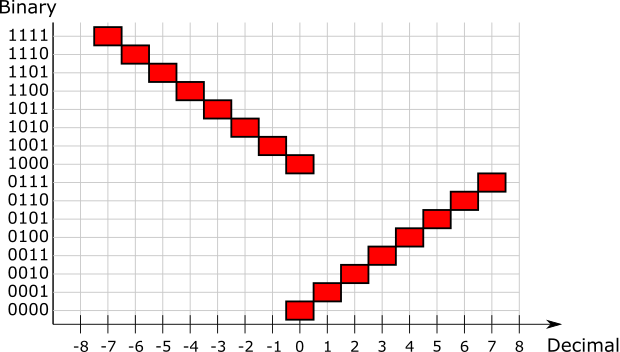
    • Sign-magnitude representation
    • Ones' complement
    • Two's complement
  • Every representation has advantages and disadvantages in terms of
    • the symmetry of the representable range of values
    • the one-to-one correspondence of the representation
    • the execution of arithmetic operations

Sign-Magnitude Representation

  • The most significant bit is used for the sign:
    • 0 = number positive; 1 = number negative
  • The remaining bits are used for the magnitude
  • In this way, a symmetrical range of values of $[-(2^{n-1}-1),+(2^{n-1}-1)]$ can be represented
  • Example for $n=4$:
Decimal01234567
Binary00000001001000110100010101100111
Decimal-0-1-2-3-4-5-6-7
Binary10001001101010111100110111101111

Sign-Magnitude Representation

  • The representation is not a one-to-one mapping because zero is represented twice. This leads to problems when testing for equality: $-0 \ne 0$
sign_magnitude

Sign-Magnitude Representation

  • The addition/subtraction is more complicated because the sign bit has to be handled separately. Otherwise:
    $ \begin{aligned} \begin{aligned} 5& \\ +-6& \\ \hline =-1&\\ \end{aligned} && \begin{aligned} 0101&&(5)\\ +1110&&(-6)\\ \hline =10011&&(-3)\\ \end{aligned} \end{aligned} $
Source:D. W. Hoffmann: Grundlagen der Technischen Informatik, 2. Auflage; Hanser 2009

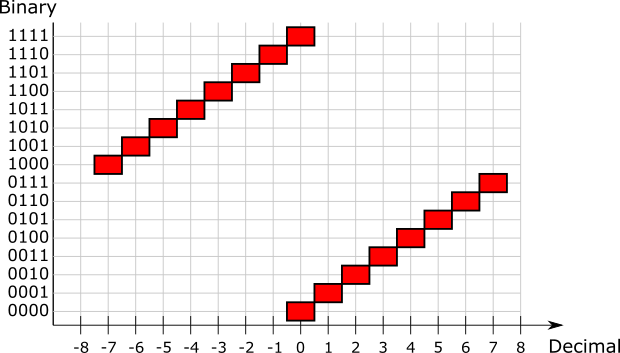
Ones' Complement

  • A negative number $(-w)$ is represented in binary by the bitwise complement of the corresponding positive
    number $w$
    • Example: $(6)_{10} \hat{=} 0110 \rightarrow (-6)_{10} \hat{=} 1001$
  • In total, a symmetrical value range of $[-(2^{n-1}-1),+(2^{n-1}-1)]$ can be represented
  • Example for $n=4$:
Decimal01234567
Binary00000001001000110100010101100111
Decimal-0-1-2-3-4-5-6-7
Binary11111110110111001011101010011000

Ones' Complement

  • The representation is not a one-to-one mapping because zero is represented twice
ones_complement

Ones' Complement

  • The addition/subtraction must be done in two steps
    • 1. Normal binary addition
    • 2. Extra addition of the carry (a carry occurring at the 2nd addition is ignored)
  • Example 1:
    $ \begin{aligned} \begin{aligned} 5& \\ +-6& \\ \hline =-1&\\ \end{aligned} && \begin{aligned} 0101&&(5)\\ +1001&&(-6)\\ \hline =1110&&(-1)\\ \end{aligned} \end{aligned} $
  • Example 2:
    $ \begin{aligned} \begin{aligned} 5& \\ +-3& \\ \hline =\ \ \ 2&\\ \end{aligned} && \begin{aligned} 0101&&(5)\\ +1100&&(-3)\\ \hline =1|0001&&(-14)\\ + 1&&(1) \\ \hline =\not{1}|0010&& (2) \end{aligned} \end{aligned} $
Source: D. W. Hoffmann: Grundlagen der Technischen Informatik, 2. Auflage; Hanser 2009

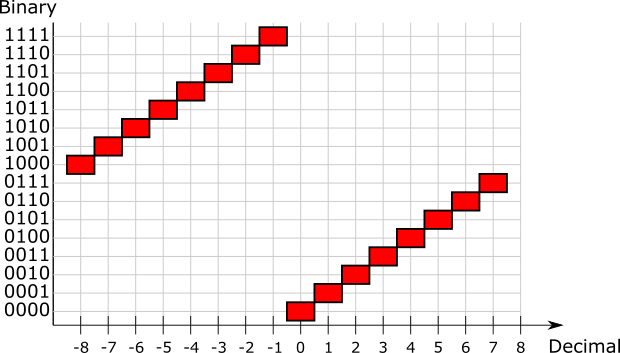
Two's Complement

  • The two's complement is formed by calculating the one's complement and adding 1
    • Example:
      $(-6)_{10} \hat{=} \,\mbox{not}(0110) + 1 = \ 1001 + 1 = 1010$
  • The range of values is asymmetric $[-2^{n-1},+2^{n-1}-1]$
  • Example for $n=4$:
Decimal01234567
Binary00000001001000110100010101100111
Decimal-1-2-3-4-5-6-7-8
Binary11111110110111001011101010011000

Two's Complement

  • The representation is a one-to-one mapping
twos_complement

Two's Complement

  • The normal unsigned integer binary addition can be used for addition/subtraction
  • Subtraction corresponds to negation and subsequent addition, e.g. $(5-6) = (5 + (-6))$
  • Example 1:
    $ \begin{aligned} \begin{aligned} 5& \\ +-6& \\ \hline =-1&\\ \end{aligned} && \begin{aligned} 0101&&(5)\\ +1010&&(-6)\\ \hline =1111&&(-1)\\ \end{aligned} \end{aligned}$
  • Example 2:
    $ \begin{aligned} \begin{aligned} 5& \\ +-3& \\ \hline =\ \ \ 2&\\ \end{aligned} && \begin{aligned} 0101&&(5)\\ +1101&&(-3)\\ \hline =\not{1}|0010&& (2) \end{aligned} \end{aligned} $

Two's Complement

  • Example 3:
    $ \begin{aligned} \begin{aligned} 4& \\ +-3& \\ \hline =\ \ \ 1&\\ \end{aligned} && \begin{aligned} 0100&&(4)\\ +1101&&(-3)\\ \hline =\not{1}|0001&&(1)\\ \end{aligned} \end{aligned}$
  • Example 4:
    $ \begin{aligned} \begin{aligned} -3& \\ +-4& \\ \hline =-7&\\ \end{aligned} && \begin{aligned} 1101&&(-3)\\ +1100&&(-4)\\ \hline =\not{1}|1001&& (-7) \end{aligned} \end{aligned} $
  • It appears that (unlike with the one's complement) we can simply omit the carry in the two's complement.
  • Is this always the case?

Two's Complement

  • Actually, yes, but be careful:
  • Example 5:
    $ \begin{aligned} \begin{aligned} -4& \\ +-5& \\ \hline =-9&\\ \end{aligned} && \begin{aligned} 1100&&(-4)\\ +1011&&(-5)\\ \hline =\not{1}|0111&&(7)\\ \end{aligned} \end{aligned} $
  • Example 6:
    $ \begin{aligned} \begin{aligned} 4& \\ +5& \\ \hline =9&\\ \end{aligned} && \begin{aligned} 0100&&(4)\\ +0101&&(5)\\ \hline =1001&&(-7)\\ \end{aligned} \end{aligned} $
  • In this case, the result is always incorrect. The carry can only be ignored if there is no overflow, i.e. the result does not go beyond the range of representable numbers.

Two's Complement

  • Example 5 again, now with $n=5$
    $ \begin{aligned} \begin{aligned} -4& \\ +-5& \\ \hline =-9&\\ \end{aligned} && \begin{aligned} 11100&&(-4)\\ +11011&&(-5)\\ \hline =\not{1}|10111&&(-9)\\ \end{aligned} \end{aligned} $
  • Example 6 again, now with $n=5$:
    $ \begin{aligned} \begin{aligned} 4& \\ +5& \\ \hline =9&\\ \end{aligned} && \begin{aligned} 00100&&(4)\\ +00101&&(5)\\ \hline =01001&&(9)\\ \end{aligned} \end{aligned} $
  • If there are enough binary digits (no overflow), the carry can be omitted

Two's Complement

  • For the two's complement, the numerical value $w$ is formally calculated as follows from the digits $z_{n-1}, \dots, z_1, z_0$ of a binary number:
    $w = -z_{n-1} \cdot 2^{n-1} + z_{n-2} \cdot 2^{n-2} + \dots + \ z_0 \cdot 2^0$
    • Example:
      $1101 = -1 \cdot 8 + 1 \cdot 4 + 0 \cdot 2 + 1 \cdot 1 = -3$

When does an overflow occur in two's complement?

  • Let us consider the addition of $w_a$ and $w_b$ with:
    $\begin{align} w_a &= -a_{n-1} \cdot 2^{n-1} + a_{n-2} \dots 2^{n-2} + \dots + \ a_0 \cdot 2^0\\ w_b &= -b_{n-1} \cdot 2^{n-1} + b_{n-2} \dots 2^{n-2} + \dots + \ b_0 \cdot 2^0\end{align}$
  • Let $c_{n-1}$ be a possible carry resulting from the binary addition of the digits $a_{n-1}$ and $b_{n-1}$, and $c_{n-2}$ a possible carry for $a_{n-2}$ and $b_{n-2}$
Sign $w_a$ Sign $w_b$ Correct result when Overflow (incorrect result) when
+ + $c_{n-1}=0$ und $c_{n-2}=0$ $c_{n-1}=0$ und $c_{n-2}=1$
+ - $c_{n-1}= c_{n-2}$ never
- + $c_{n-1}= c_{n-2}$ never
- - $c_{n-1}=1$ und $c_{n-2}=1$ $c_{n-1}=1$ und $c_{n-2}=0$
  • With two positive numbers, an overflow occurs when the carry in the most significant digit corrupts the sign bit of the sum
  • With two negative numbers, an overflow occurs if the inversion of the sign bit is not compensated by a carry in the most significant digit
  • Later we will learn that an overflow can be detected by an XOR, i.e. an overflow occurs when ($c_{n-1}$ xor $c_{n-2}$) = 1

Inverse of the Two's Complement

  • The inverse operation of the two's complement is simply a renewed application of the two's complement
    • Example:
      $\begin{aligned}(6)_{10} &\hat{=} \ 0110 \\ (-6)_{10} &\hat{=} \,\mbox{not}(0110) + 1 = 1001 + 1 = 1010\\ (6)_{10} &\hat{=} \,\mbox{not}(1010) + 1 = (0101) + 1 = 0110\end{aligned}$
  • This means that every application of the two's complement negates the represented decimal number

Representation of Signed Integer Numbers

  • Summary
RepresentationRangeOne-to-one mappingMath Operations
Sign-magnitude symmetricnoSpecial treatment
Ones' complementsymmetricno2-step addition
Two's complementasymmetricyesSimple
  • The two's complement is the predominant method in practice for representing binary signed integer numbers (a lack of symmetry is tolerated)
BytesBitsRangeName of the data type (Microsoft Visual C++)
18$[–128;127]$char
216$[–32768;32767]$short
432$[–2147483648;2147483647]$int
864$\begin{align} [-&9223372036854775808; \\ &9223372036854775807\ \ ] \end{align}$long long
Source: Data Type Ranges, Visual Studio 2013

Representation of Signed Rational Numbers

  • We consider two methods for the binary representation of signed rational numbers:
    • Fixed-point representation
    • Floating-point representation

Fixed-Point Representation

  • The fixed-point representation is similar to the sign-magnitude representation of integer numbers
  • The most significant bit $s$ is used for the sign
  • The remaining $n-1$ bits are called the mantissa and are used to store the integer and fractional parts.
  • Example for $n=16$:
    fixedpoint
  • In the mantissa, the first $k \leq (n-1)$ digits are set as the digits before the decimal point. This results in $j = (n-1) - k$ digits after the decimal point
  • The numerical value $w$ is then calculated as follows:
    $w = (-1)^{s}\left(\left(\sum\limits_{i=0}^{k-1} m_{j+i} \cdot 2^i\right) + \left(\sum\limits_{i=-j}^{-1} m_{j+i} \cdot 2^i\right)\right) = (-1)^{s}\left(\sum\limits_{i=-j}^{k-1} m_{j+i} \cdot 2^i\right)$

Fixed-Point Representation

  • Example: Conversion of $11011001$ for $n=8$, $k=4$ and $j=3$:
    fixedpointexample
    $\begin{align} w &= (-1)^{s}\left(\sum\limits_{i=-j}^{k-1} m_{j+i} \cdot 2^i\right) \\ &= (-1)^{1} \left(1 \cdot 2^{-3}+ 0 \cdot 2^{-2} + 0 \cdot 2^{-1} + 1 \cdot 2^{0} + 1 \cdot 2^{1} + 0 \cdot 2^{2} + 1 \cdot 2^{3}\right) \\ &= (-1) \left(0.125 + 1 + 2 + 8\right) = -11.125\end{align}$
  • Fixed-point representation is an equidistant number format because the numerical distance between two representable numbers is constant
  • If the range of numerical values used is very similar and known in advance, a fixed-point representation can thus guarantee a certain accuracy of the representation
  • The fixed-point representation is therefore used by special hardware, such as digital signal processors (DSPs)

Floating-Point Representation

  • In practice, numbers with different orders of magnitude have to be processed
  • As an example, physical constants can be examined:
    • Speed of light: $2.99792458 \cdot 10^{8}$ m/s
    • Electron mass: $9.10938291 \cdot 10^{−31}$ kg
    • Elementary charge: $1.60217656 \cdot 10^{−19}$ C
  • In scientific notation, the decimal point is shifted by the exponent:
    • Shift to the right for small numbers: $0.00041 = 4.1 \cdot 10^{−4}$
    • Shift to the left for large numbers: $1200000.00041 \approx 1.2 \cdot 10^{6}$
  • The binary floating point representation copies the scientific notation and extends the fixed-point representation by a binary-coded exponent

Floating-Point Representation

  • Example: 1 bit sign, 5 bit exponent, 10 bit mantissa
    floatingpoint
  • The 5 bits of the exponent can represent $2^5=32$ different numbers
  • To represent negative exponents, instead of the exponent $e$, a "biased exponent" $c\ge0$ is stored in the 5 bits:
    floatingpointchara
  • The conversion between the "biased exponent" and the exponent is done by subtracting a constant, e.g. $e = c - 15$
  • This means that the exponent can represent values from the interval $[-15,16]$

Floating-Point Representation

  • At first, the floating-point representation is not uniquely defined
    $\begin{align}0.00111011 &= 000001.11011 \cdot 2^{-3}\\ &= 00000.111011 \cdot 2^{-2}\\ &= 0000.0111011 \cdot2^{-1}\\ &= 000.00111011 \cdot2^{0}\\ &= 00.000111011 \cdot2^{1}\\ &= 0.0000111011 \cdot2^{2}\\ &= \dots \end{align}$
  • In the normalized form, the exponent is chosen such that the first digit before the decimal point is unequal 0, in this case $000001.11011 \cdot 2^{-3}$
  • In the modified normalized form, the exponent is chosen so that the first digit after the decimal point is not equal to 0, in this case $00000.111011 \cdot 2^{-2}$
  • In a normalized form, the most significant bit is always 1. This "implicit leading one" can therefore be omitted in a so-called packed form

Floating-Point Representation

floatingpointchara
  • Example 1: $1001011010000000$ (modified normalized, not packed)
    $\begin{align}s &= 1 \\ e &= c - (15)_{10} = (00101)_2 - (15)_{10} = (5)_{10} - (15)_{10} = -10 \\ m &= 0.1010000000 = 1 \cdot 2^{-1} + 1 \cdot 2^{-3} = 0.5 + 0.125 = 0.625 \end{align}$

    Result: $-0.625 \cdot 2^{-10}$
  • Example 2: $1001011010000000$ (normalized, not packed)
    $\begin{align}s &= 1 \\ e &= c - (15)_{10} = (00101)_2 - (15)_{10} = (5)_{10} - (15)_{10} = -10 \\ m &= 1.010000000 = 1 \cdot 2^{0} + 1 \cdot 2^{-2} = 1 + 0.25 = 1.25 \end{align}$

    Result: $-1.25 \cdot 2^{-10}$

Floating-Point Representation

floatingpointchara
  • Example 3: $0101011010000000$ (modified normalized, packed)
    $\begin{align}s &= 0 \\ e &= c - (15)_{10} = (10101)_2 - (15)_{10} = (21)_{10} - (15)_{10} = (6)_{10} \\ m &= 0.11010000000 = \\ &=1 \cdot 2^{-1} + 1 \cdot 2^{-2} + 1 \cdot 2^{-4} = 0.5 + 0.25 + 0.0625= 0.8125 \end{align}$
    Result: $0.8125 \cdot 2^{6}$
  • Example 4: $0101011010000000$ (normalized, packed)
    $\begin{align}s &= 0 \\ e &= c - (15)_{10} = (10101)_2 - (15)_{10} = (21)_{10} - (15)_{10} = (6)_{10} \\ m &= 1.1010000000 = \\ &=1 \cdot 2^{0} + 1 \cdot 2^{-1} + 1 \cdot 2^{-3} = 1 + 0.5 + 0.125= 1.625 \end{align}$
    Result: $1.625 \cdot 2^{6}$

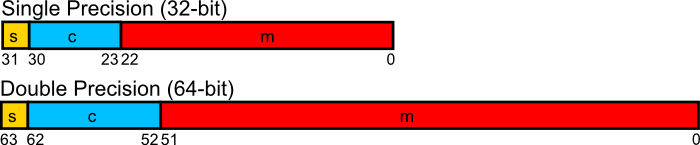
Floating-Point Representation: IEEE 754 Formats

ieee754
Biased exponent $c$Mantissa $m$32-/64-bit Precision
$000\dots0000$arbitrary32: $(-1)^s 0.m \cdot 2^{-126}$
64: $(-1)^s 0.m \cdot 2^{-1022}$
$ 111\dots1111$$=0$$(-1)^s \cdot \infty$
$ 111\dots1111$$\ne0$Not a Number (NaN)
all other bit sequences (default)arbitrary32: $(-1)^s 1.m \cdot 2^{c-127}$
64: $(-1)^s 1.m \cdot 2^{c-1023}$
Source:D. W. Hoffmann: Grundlagen der Technischen Informatik, 2. Auflage; Hanser 2009

Floating-Point Representation: IEEE 754 Formats

  • The IEEE 754 formats (from 1985) are supported by all standard microprocessors today
  • Normally, the packed normalized form is used
  • Some reserved bit patterns for the "biased exponent" $c$ have special meaning:
  • Null
    • $c=000\dots0000$ switches to an unpacked modified normalized form
    • Representation of zero by $m=0$
  • Infinity
    • Biased exponent $c=1111\dots111$ and $m=0$
    • The sign $s$ decides between $+\infty$ and $-\infty$
    • This occurs, for example, when dividing by $0$
  • Not a Number (NaN)
    • Biased exponent $c=1111\dots111$ und $m\ne0$
    • This occurs during algebraic operations with undefined or unrepresentable results, such as $0/0$, $0\cdot \infty$, etc.

Floating-Point Representation: IEEE 754 Formats

  • For the representation of floating point numbers in source code, the notation "52.21e-2" or "52.21E-2" is typically used. The number after the "e" indicates the exponent of the power of ten
  • This notation is also common in many programming languages
BytesBitsRange of valuesName of data type
432± 1.4e-45 ... 3.403e38 float
864± 4.94e-324 ... 1.798e308double

Are there any questions?

questions

Please notify me by e-mail if you have questions, suggestions for improvement, or found typos: Contact

More lecture slides

Slides in German (Folien auf Deutsch)

Legal Notice, Privacy Policy,