Steuerungstasten

→ nächste Folie (auch Enter oder Spacebar).
← vorherige Folie
 d  schaltet das Zeichnen auf Folien ein/aus
 p  wechselt zwischen Druck- und Präsentationsansicht
CTRL  +  vergrößert die Folien
CTRL  -  verkleinert die Folien
CTRL  0  setzt die Größenänderung zurück

Das Weiterschalten der Folien kann ebenfalls durch das Klicken auf den rechten bzw. linken Folienrand erfolgen.

Notation

Typ Schriftart Beispiele
Variablen (Skalare) kursiv $a, b, x, y$
Funktionen aufrecht $\mathrm{f}, \mathrm{g}(x), \mathrm{max}(x)$
Vektoren fett, Elemente zeilenweise $\mathbf{a}, \mathbf{b}= \begin{pmatrix}x\\y\end{pmatrix} = (x, y)^\top,$ $\mathbf{B}=(x, y, z)^\top$
Matrizen Schreibmaschine $\mathtt{A}, \mathtt{B}= \begin{bmatrix}a & b\\c & d\end{bmatrix}$
Mengen kalligrafisch $\mathcal{A}, B=\{a, b\}, b \in \mathcal{B}$
Zahlenbereiche, Koordinatenräume doppelt gestrichen $\mathbb{N}, \mathbb{Z}, \mathbb{R}^2, \mathbb{R}^3$

Inhalt

  • Darstellung vorzeichenloser ganzer Zahlen
  • Darstellung vorzeichenbehafteter ganzer Zahlen
    • Betrags-Vorzeichendarstellung
    • Einerkomplement
    • Zweierkomplement
  • Darstellung vorzeichenbehafteter rationaler Zahlen
    • Festkommadarstellung
    • Gleitkommadarstellung

Darstellung vorzeichenloser ganzer Zahlen

  • Je nachdem wie viele Bits zur binären Speicherung einer vorzeichenloser ganzer Zahlen (unsigned integer) zur Verfügung gestellt werden, können verschieden große Zahlen dargestellt werden
BytesBitsWertebereichName des Datentyps (Microsoft Visual C++)
18$[0;255]$unsigned char
216$[0;65535]$unsigned short
432$[0;4294967295]$unsigned int
864$[0;18446744073709551615]$unsigned long long
Quelle: Data Type Ranges, Visual Studio 2013

Big- und Little-Endian-Speicherung

  • Little-Endian
    • Das Byte mit der niedrigsten Wertigkeit wird zuerst gespeichert
    • Alle x86-kompatiblen Rechner verwenden diese Ordnung
little endian
  • Big-Endian
    • Das Byte mit der niedrigsten Wertigkeit wird zuletzt gespeichert
    • MIPS, SPARC, PowerPC, Java Virtual Machine, etc.
big endian

Darstellung vorzeichenbehafteter ganzer Zahlen

  • Sollen positive und negative Zahlen gespeichert werden, so gibt es verschiedene Möglichkeiten:
    • Betrags-Vorzeichendarstellung
    • Einerkomplement
    • Zweierkomplement
  • Jede Darstellung hat Vor- und Nachteile bezüglich
    • der Symmetrie des darstellbaren Wertebereichs
    • der Eineindeutigkeit der Darstellung
    • der Durchführung von arithmetischen Operationen

Betrags-Vorzeichendarstellung

  • Das höchstwertige Bit wird für das Vorzeichen verwendet:
    • 0 = Zahl positiv; 1 = Zahl negativ
  • Die verbleibenden Bits werden für den Betrag verwendet.
  • Insgesamt kann so ein symmetrischer Wertebereich von $[-(2^{n-1}-1),+(2^{n-1}-1)]$ dargestellt werden
  • Beispiel für $n=4$:
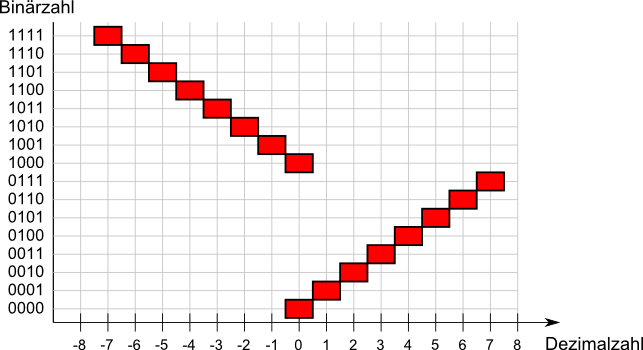
Dezimal01234567
Binär00000001001000110100010101100111
Dezimal-0-1-2-3-4-5-6-7
Binär10001001101010111100110111101111

Betrags-Vorzeichendarstellung

  • Die Darstellung ist nicht eineindeutig, da die Null doppelt repräsentiert ist. Dies führt zu Problemen beim Gleichheitstest: $-0 \ne 0$
sign_magnitude

Betrags-Vorzeichendarstellung

  • Die Addition/Subtraktion ist umständlich, da das Vorzeichen-Bit gesondert behandelt werden muss, ansonsten:
    $ \begin{aligned} \begin{aligned} 5& \\ +-6& \\ \hline =-1&\\ \end{aligned} && \begin{aligned} 0101&&(5)\\ +1110&&(-6)\\ \hline =10011&&(-3)\\ \end{aligned} \end{aligned} $
Quelle:D. W. Hoffmann: Grundlagen der Technischen Informatik, 2. Auflage; Hanser 2009

Einerkomplement

  • Eine negative Zahl $-w$ wird binär durch das bitweise Komplement der entsprechenden positiven Zahl $w$ dargestellt
    • Beispiel: $(6)_{10} \hat{=} 0110 \rightarrow (-6)_{10} \hat{=} 1001$
  • Insgesamt kann so ein symmetrischer Wertebereich von $[-(2^{n-1}-1),+(2^{n-1}-1)]$ dargestellt werden
  • Beispiel für $n=4$:
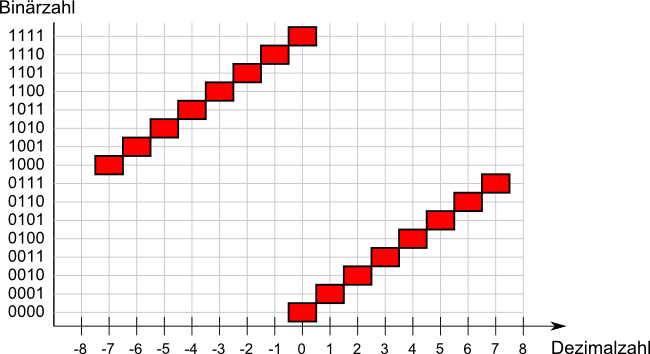
Dezimal01234567
Binär00000001001000110100010101100111
Dezimal-0-1-2-3-4-5-6-7
Binär11111110110111001011101010011000

Einerkomplement

  • Die Darstellung ist nicht eineindeutig, da die Null doppelt repräsentiert ist.
ones_complement

Einerkomplement

  • Die Addition/Subtraktion muss in zwei Schritten erfolgen
    • 1. Normale Binäraddition
    • 2. Zusätzliche Addition eines eventuellen Übertrags (die bei der 2. Addition entstehenden Überträge werden gestrichen)
  • Beispiel 1:
    $ \begin{aligned} \begin{aligned} 5& \\ +-6& \\ \hline =-1&\\ \end{aligned} && \begin{aligned} 0101&&(5)\\ +1001&&(-6)\\ \hline =1110&&(-1)\\ \end{aligned} \end{aligned} $
  • Beispiel 2:
    $ \begin{aligned} \begin{aligned} 5& \\ +-3& \\ \hline =\ \ \ 2&\\ \end{aligned} && \begin{aligned} 0101&&(5)\\ +1100&&(-3)\\ \hline =1|0001&&(-14)\\ + 1&&(1) \\ \hline =\not{1}|0010&& (2) \end{aligned} \end{aligned} $
    • Quelle:D. W. Hoffmann: Grundlagen der Technischen Informatik, 2. Auflage; Hanser 2009

Zweierkomplement

  • Beim Zweierkomplement werden die negativen Zahlen durch Bestimmung des Einerkomplements und einer zusätzlichen Addition von 1 gebildet
    • Beispiel:
      $(-6)_{10} \hat{=} \,\mbox{not}(0110) + 1 = \ 1001 + 1 = 1010$
  • Wertebereich wird unsymmetrisch $[-2^{n-1},+2^{n-1}-1]$
  • Beispiel für $n=4$:
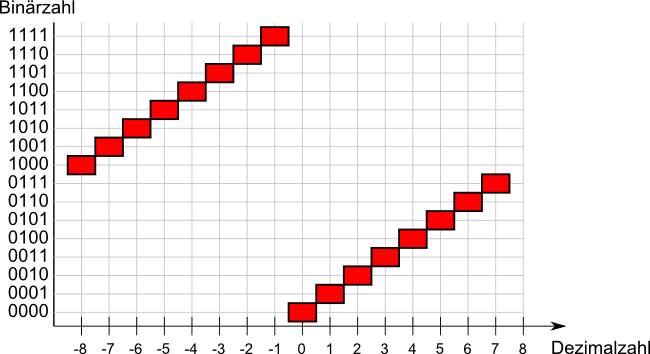
Dezimal01234567
Binär00000001001000110100010101100111
Dezimal-1-2-3-4-5-6-7-8
Binär11111110110111001011101010011000

Zweierkomplement

  • Die Darstellung ist eineindeutig
twos_complement

Zweierkomplement

  • Zur Addition/Subtraktion kann die normale vorzeichenlose Binäraddition verwendet werden
  • Subtraktion entspricht Negation und anschließender Addtion, um z.B. $(5-6) = (5 + (-6))$
  • Beispiel 1:
    $ \begin{aligned} \begin{aligned} 5& \\ +-6& \\ \hline =-1&\\ \end{aligned} && \begin{aligned} 0101&&(5)\\ +1010&&(-6)\\ \hline =1111&&(-1)\\ \end{aligned} \end{aligned}$
  • Beispiel 2:
    $ \begin{aligned} \begin{aligned} 5& \\ +-3& \\ \hline =\ \ \ 2&\\ \end{aligned} && \begin{aligned} 0101&&(5)\\ +1101&&(-3)\\ \hline =\not{1}|0010&& (2) \end{aligned} \end{aligned} $

Zweierkomplement

  • Beispiel 3:
    $ \begin{aligned} \begin{aligned} 4& \\ +-3& \\ \hline =\ \ \ 1&\\ \end{aligned} && \begin{aligned} 0100&&(4)\\ +1101&&(-3)\\ \hline =\not{1}|0001&&(1)\\ \end{aligned} \end{aligned}$
  • Beispiel 4:
    $ \begin{aligned} \begin{aligned} -3& \\ +-4& \\ \hline =-7&\\ \end{aligned} && \begin{aligned} 1101&&(-3)\\ +1100&&(-4)\\ \hline =\not{1}|1001&& (-7) \end{aligned} \end{aligned} $
  • Es scheint als könnten wir (anders als beim Einerkomplement) den Übertrag beim Zweierkomplement einfach streichen.
  • Ist diese immer der Fall?

Zweierkomplement

  • Eigentlich ja, aber Vorsicht:
  • Beispiel 5:
    $ \begin{aligned} \begin{aligned} -4& \\ +-5& \\ \hline =-9&\\ \end{aligned} && \begin{aligned} 1100&&(-4)\\ +1011&&(-5)\\ \hline =\not{1}|0111&&(7)\\ \end{aligned} \end{aligned} $
  • Beispiel 6:
    $ \begin{aligned} \begin{aligned} 4& \\ +5& \\ \hline =9&\\ \end{aligned} && \begin{aligned} 0100&&(4)\\ +0101&&(5)\\ \hline =1001&&(-7)\\ \end{aligned} \end{aligned} $
  • Hier kommt es jeweils zum falschen Ergebnis. Der Übertrag kann nur gestrichen werden, wenn es nicht zum Überlauf kommt, d.h. das Ergebnis den Bereich der darstellbaren Zahlen nicht verlässt

Zweierkomplement

  • Nochmal Beispiel 5, jetzt mit $n=5$
    $ \begin{aligned} \begin{aligned} -4& \\ +-5& \\ \hline =-9&\\ \end{aligned} && \begin{aligned} 11100&&(-4)\\ +11011&&(-5)\\ \hline =\not{1}|10111&&(-9)\\ \end{aligned} \end{aligned} $
  • Nochmal Beispiel 6, jetzt mit $n=5$:
    $ \begin{aligned} \begin{aligned} 4& \\ +5& \\ \hline =9&\\ \end{aligned} && \begin{aligned} 00100&&(4)\\ +00101&&(5)\\ \hline =01001&&(9)\\ \end{aligned} \end{aligned} $
  • Bei ausreichender Anzahl von Stellen (kein Überlauf) kann der Übertrag gestrichen werden

Zweierkomplement

  • Beim Zweierkomplement berechnet sich der Zahlenwert $w$ formal wie folgt als den Ziffern $z_{n-1}, \dots, z_1, z_0$ einer Binärzahl:
    $w = -z_{n-1} \cdot 2^{n-1} + z_{n-2} \cdot 2^{n-2} + \dots + \ z_0 \cdot 2^0$
    • Beispiel:
      $1101 = -1 \cdot 8 + 1 \cdot 4 + 0 \cdot 2 + 1 \cdot 1 = -3$

Wann kommt es beim Zweierkomplement zum Überlauf?

  • Betrachten wir die Addition von $w_a$ und $w_b$ mit:
    $\begin{align} w_a &= -a_{n-1} \cdot 2^{n-1} + a_{n-2} \dots 2^{n-2} + \dots + \ a_0 \cdot 2^0\\ w_b &= -b_{n-1} \cdot 2^{n-1} + b_{n-2} \dots 2^{n-2} + \dots + \ b_0 \cdot 2^0\end{align}$
  • Sei $c_{n-1}$ ein eventueller Übertrag, der aus der binären Addition der Stellen $a_{n-1}$ und $b_{n-1}$ entsteht, und $c_{n-2}$ der eventuelle Übertrag bei $a_{n-2}$ und $b_{n-2}$
Vorzeichen $w_a$ Vorzeichen $w_b$ Richtiges Ergebnis, wenn Überlauf (falsches Ergebnis), wenn
+ + $c_{n-1}=0$ und $c_{n-2}=0$ $c_{n-1}=0$ und $c_{n-2}=1$
+ - $c_{n-1}= c_{n-2}$ nie
- + $c_{n-1}= c_{n-2}$ nie
- - $c_{n-1}=1$ und $c_{n-2}=1$ $c_{n-1}=1$ und $c_{n-2}=0$
  • Bei zwei positiven Zahlen entsteht ein Überlauf, wenn der Übertrag in die letzte Stelle das Vorzeichenbit der Summe verfälscht
  • Bei zwei negativen Zahlen entsteht ein Überlauf, wenn die Umkehrung des Vorzeichenbits nicht durch einen Übertrag in die letzte Stelle kompensiert wird
  • Später werden wir lernen, dass ein Überlauf schaltungstechnisch durch ein XOR detektiert werden kann, d.h. Überlauf tritt auf, wenn ($c_{n-1}$ xor $c_{n-2}$) = 1

Inverse des Zweierkomplements

  • Die Inverse Operation des Zweierkomplements ist einfach eine erneute Anwendung des Zweierkomplements
    • Beispiel:
      $\begin{aligned}(6)_{10} &\hat{=} \ 0110 \\ (-6)_{10} &\hat{=} \,\mbox{not}(0110) + 1 = 1001 + 1 = 1010\\ (6)_{10} &\hat{=} \,\mbox{not}(1010) + 1 = (0101) + 1 = 0110\end{aligned}$
  • D.h. jede Anwendung des Zweierkomplements negiert die repräsentierte Dezimalzahl

Darstellung vorzeichenbehafteter ganzer Zahlen

  • Zusammenfassung
VerfahrenWertbereichEineindeutigOperationen
Betrags-VorzeichendarstellungsymmetrischneinSonderbehandlung
Einerkomplementsymmetrischnein2-Stufen Addition
Zweierkomplementunsymmetrischjaeinfach
  • Das Zweierkomplement ist die in der Praxis vorherschende Art zur Darstellung binärer vorzeichenbehafteter ganzer Zahlen (Unsymmetrie wird in Kauf genommen)
BytesBitsWertebereichName des Datentyps (Microsoft Visual C++)
18$[–128;127]$char
216$[–32768;32767]$short
432$[–2147483648;2147483647]$int
864$\begin{align} [-&9223372036854775808; \\ &9223372036854775807\ \ ] \end{align}$long long
Quelle: Data Type Ranges, Visual Studio 2013

Darstellung vorzeichenbehafteter rationaler Zahlen

  • Zur binären Repräsentation vorzeichenbehafteter rationaler Zahlen werden wir zwei Verfahren betrachen:
    • Festkommadarstellung
    • Gleitkommadarstellung

Festkommadarstellung

  • Die Festkommadarstellung ist ähnlich der Betrags-Vorzeichendarstellung bei ganzen Zahlen
  • Das höchstwertige Bit $s$ wird für das Vorzeichen verwendet
  • Die verbleibenden $n-1$ Bits werden als Mantisse bezeichnet und werden zur Speicherung der Vor- und Nachkommastellen verwendet
  • Beispiel für $n=16$:
    fixedpoint
  • In der Mantisse werden die ersten $k \leq (n-1)$ Stellen als Vorkommastellen festgelegt. Damit gibt es $j=(n-1)-k$ Nachkommastellen
  • Der Zahlenwert $w$ berechnet sich dann gemäß:
    $w = (-1)^{s}\left(\left(\sum\limits_{i=0}^{k-1} m_{j+i} \cdot 2^i\right) + \left(\sum\limits_{i=-j}^{-1} m_{j+i} \cdot 2^i\right)\right) = (-1)^{s}\left(\sum\limits_{i=-j}^{k-1} m_{j+i} \cdot 2^i\right)$

Festkommadarstellung

  • Beispiel: Umrechnung von $11011001$ für $n=8$, $k=4$ und $j=3$:
    fixedpointexample
    $\begin{align} w &= (-1)^{s}\left(\sum\limits_{i=-j}^{k-1} m_{j+i} \cdot 2^i\right) \\ &= (-1)^{1} \left(1 \cdot 2^{-3}+ 0 \cdot 2^{-2} + 0 \cdot 2^{-1} + 1 \cdot 2^{0} + 1 \cdot 2^{1} + 0 \cdot 2^{2} + 1 \cdot 2^{3}\right) \\ &= (-1) \left(0,125 + 1 + 2 + 8\right) = -11,125\end{align}$
  • Festkommadarstellung ist ein äquidistantes Zahlenformat, da der nummerische Abstand zwischen zwei darstellenbaren Zahlen konstant ist
  • Ist der Wertbereich der verwendeten Zahlen sehr ähnlich und vorher bekannt, kann mit einer Festkommadarstellung somit eine bestimmte Genauigkeit der Darstellung garantiert werden
  • Die Festkommadarstellung kommt daher nur bei spezieller Hardware, wie z.B. digitalen Signalprozessoren (DSPs) zum Einsatz

Gleitkommadarstellung

  • In der Praxis müssen oft Zahlen mit verschiedenen Größenordnungen verarbeitet werden
  • Als Beispiel können physikalische Naturkonstanten betrachtet werden:
    • Lichtgeschwindigkeit: $2,99792458 \cdot 10^{8}$ m/s
    • Elektronenmasse: $9,10938291 \cdot 10^{−31}$ kg
    • Elementarladung: $1,60217656 \cdot 10^{−19}$ C
  • Bei der wissenschaftlichen Potenzschreibweise wird das Komma durch den Exponenten verschoben:
    • Verschiebung nach rechts für kleine Zahlen: $0,00041 = 4,1 \cdot 10^{−4}$
    • Verschiebung nach links für große Zahlen: $1200000,00041 \approx 1,2 \cdot 10^{6}$
  • Die binäre Gleitkommadarstellung (engl. "floating point") kopiert die wissenschaftlichen Potenzschreibweise und erweitert die Festkommadarstellung um einen binär-kodierten Exponenten

Gleitkommadarstellung

  • Beispiel: 1 Bit Vorzeichen, 5 Bit Exponent, 10 Bit Mantisse
    floatingpoint
  • Die 5 Bits des Exponenten können $2^5=32$ verschiedene Zahlen darstellen
  • Um negative Exponenten $e$ darzustellen, werden statt dem Exponenten dessen Charakteristik $c>0$ in den 5 Bits gespeichert:
    floatingpointchara
  • Die Umrechnung zwischen Charakteristik und Exponenten erfolgt durch Substraktion einer Konstanten, z.B. $e = c - 15$
  • Damit kann der Exponent Werte aus dem Intervall $[-15,16]$ annehmen

Gleitkommadarstellung

  • Die Gleitkommadarstellung ist zunächst nicht eindeutig
    $\begin{align}0,00111011 &= 000001,11011 \cdot 2^{-3}\\ &= 00000,111011 \cdot 2^{-2}\\ &= 0000,0111011 \cdot2^{-1}\\ &= 000,00111011 \cdot2^{0}\\ &= 00,000111011 \cdot2^{1}\\ &= 0,0000111011 \cdot2^{2}\\ &= \dots \end{align}$
  • Bei der Nachkomma-Normalisierung wird der Exponent so gewählt, dass die erste Nachkommastelle ungleich 0 ist, hier also $00000,111011 \cdot 2^{-2}$
  • Bei der Vorkomma-Normalisierung wird der Exponent so gewählt, dass die erste Vorkommastelle ungleich 0 ist, hier also $000001,11011 \cdot 2^{-3}$
  • Bei einer normalisierten Darstellung ist bekannt, dass das erste relevante Bit immer eine 1 ist. Dieses Bit kann daher in einer sogenannten gepackten Darstellung weggelassen werden.

Gleitkommadarstellung

floatingpointchara
  • Bespiel 1: $1001011010000000$ (Nachkomma-Normalisierung, ungepackt)
    $\begin{align}s &= 1 \\ e &= c - (15)_{10} = (00101)_2 - (15)_{10} = (5)_{10} - (15)_{10} = -10 \\ m &= 0,1010000000 = 1 \cdot 2^{-1} + 1 \cdot 2^{-3} = 0,5 + 0,125 = 0,625 \end{align}$

    Ergebnis: $-0,625 \cdot 2^{-10}$
  • Bespiel 2: $1001011010000000$ (Vorkomma-Normalisierung, ungepackt)
    $\begin{align}s &= 1 \\ e &= c - (15)_{10} = (00101)_2 - (15)_{10} = (5)_{10} - (15)_{10} = -10 \\ m &= 1,010000000 = 1 \cdot 2^{0} + 1 \cdot 2^{-2} = 1 + 0,25 = 1,25 \end{align}$

    Ergebnis: $-1,25 \cdot 2^{-10}$

Gleitkommadarstellung

floatingpointchara
  • Bespiel 3: $0101011010000000$ (Nachkomma-Normalisierung, gepackt)
    $\begin{align}s &= 0 \\ e &= c - (15)_{10} = (10101)_2 - (15)_{10} = (21)_{10} - (15)_{10} = (6)_{10} \\ m &= 0,11010000000 = \\ &=1 \cdot 2^{-1} + 1 \cdot 2^{-2} + 1 \cdot 2^{-4} = 0,5 + 0,25 + 0,0625= 0,8125 \end{align}$
    Ergebnis: $0,8125 \cdot 2^{6}$
  • Bespiel 4: $0101011010000000$ (Vorkomma-Normalisierung, gepackt)
    $\begin{align}s &= 0 \\ e &= c - (15)_{10} = (10101)_2 - (15)_{10} = (21)_{10} - (15)_{10} = (6)_{10} \\ m &= 1,1010000000 = \\ &=1 \cdot 2^{0} + 1 \cdot 2^{-1} + 1 \cdot 2^{-3} = 1 + 0,5 + 0,125= 1,625 \end{align}$
    Ergebnis: $1,625 \cdot 2^{6}$

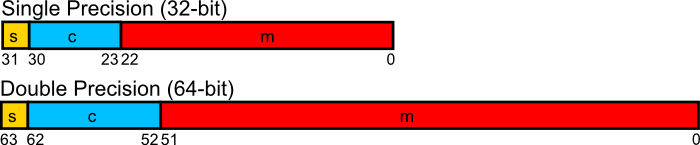
Gleitkommadarstellung: IEEE 754 Formate

ieee754
Charakteristik $c$Mantisse $m$32-/64-bit Precision
$000\dots0000$beliebig32: $(-1)^s 0,m \cdot 2^{-126}$
64: $(-1)^s 0,m \cdot 2^{-1022}$
$ 111\dots1111$$=0$$(-1)^s \cdot \infty$
$ 111\dots1111$$\ne0$Not a Number (NaN)
alle anderen Bitfolgen (default)beliebig32: $(-1)^s 1,m \cdot 2^{c-127}$
64: $(-1)^s 1,m \cdot 2^{c-1023}$
Quelle:D. W. Hoffmann: Grundlagen der Technischen Informatik, 2. Auflage; Hanser 2009

Gleitkommadarstellung: IEEE 754 Formate

  • Die IEEE 754 Formate (aus dem Jahre 1985) werde heutzutage von allen gängigen Mikroprozessoren unterstützt
  • Normalerweise gepackte Darstellung mit Vorkomma-Normalisierung
  • Es gibt einige reservierte Bitmuster für die Charakteristik mit Sonderbedeutung:
  • Null
    • Charakteristik $c=000\dots0000$ schaltet in eine ungepackte Darstellung um
    • Darstellung der Null durch $m=0$
  • Unendlich
    • Charakteristik $c=1111\dots111$ und $m=0$
    • Vorzeichen $s$ entscheidet zwischen $+\infty$ und $-\infty$
    • Entsteht z.B. bei Division durch $0$
  • Not a Number (NaN)
    • Charakteristik $c=1111\dots111$ und $m\ne0$
    • Entsteht bei algebraischen Operationen mit undefiniertem oder nicht repräsentierbarem Ergebnis, wie z.B. $0/0$, $0\cdot \infty$, usw.

Gleitkommadarstellung: IEEE 754 Formate

  • Für die Darstellung von Gleitpunktzahlen in einem (Quell-)Text wird typischerweise die Notation "52.21e-2" oder "52.21E-2" verwendet. Die Zahl hinter dem "E" gibt den Exponenten der Zehnerpotenz an.
  • Diese Notation ist auch in vielen Programmiersprachen üblich
  • Anstatt des deutschen Kommas wird im Englischen (und daher in fast allen Programmiersprachen) der Dezimalpunkt verwendet
  • Größenordnungen:
BytesBitsWertebereichName des Datentyps
432± 1.4e-45 ... 3.403e38 float
864± 4.94e-324 ... 1.798e308double

Gibt es Fragen?

questions

Anregungen oder Verbesserungsvorschläge können auch gerne per E-mail an mich gesendet werden: Kontakt


Weitere Vorlesungsfolien

Impressum, Datenschutz,