Steuerungstasten

→ nächste Folie (auch Enter oder Spacebar).
← vorherige Folie
 d  schaltet das Zeichnen auf Folien ein/aus
 p  wechselt zwischen Druck- und Präsentationsansicht
CTRL  +  vergrößert die Folien
CTRL  -  verkleinert die Folien
CTRL  0  setzt die Größenänderung zurück

Das Weiterschalten der Folien kann ebenfalls durch das Klicken auf den rechten bzw. linken Folienrand erfolgen.

Notation

Typ Schriftart Beispiele
Variablen (Skalare) kursiv $a, b, x, y$
Funktionen aufrecht $\mathrm{f}, \mathrm{g}(x), \mathrm{max}(x)$
Vektoren fett, Elemente zeilenweise $\mathbf{a}, \mathbf{b}= \begin{pmatrix}x\\y\end{pmatrix} = (x, y)^\top,$ $\mathbf{B}=(x, y, z)^\top$
Matrizen Schreibmaschine $\mathtt{A}, \mathtt{B}= \begin{bmatrix}a & b\\c & d\end{bmatrix}$
Mengen kalligrafisch $\mathcal{A}, B=\{a, b\}, b \in \mathcal{B}$
Zahlenbereiche, Koordinatenräume doppelt gestrichen $\mathbb{N}, \mathbb{Z}, \mathbb{R}^2, \mathbb{R}^3$

Inhalt

  • Minterm und Maxterm
  • Disjunktive Normalform
  • Konjunktive Normalform
  • Zusammenhang zwischen den Normalformen
  • Realisierung durch Logikgatter

Normalformen

  • Die Wahrheitstabelle ist eine eindeutige Definition einer booleschen Funktion
  • Es gibt jedoch unendlich viele verschiedene Realisierungen mittels Logikgattern oder Beschreibungen in Form eines booleschen Ausdrucks
  • Normalformen (auch kanonische Formen):
    • Standarddarstellung für einen booleschen Ausdruck in einer eindeutigen algebraischen Form

Minterm

  • Gegeben sei eine boolesche Funktion $y = f(x_n, \dots, x_1, x_0)$ und die Literale $\hat{x}_i \in \{\overline{x}_i, x_i\}$.
  • Minterm: $(\hat{x}_n \land \dots \land \hat{x}_2 \land \hat{x}_1 \land \hat{x}_0)$
    • Der Minterm evaluiert für genau eine bestimmte Konfiguration der Variablen $x_i$ zu 1 und sonst zu 0
    • Genauer gesagt: Der Minterm evaluiert genau dann zu 1, wenn für alle negierten Variablen $x_i=0$ und alle nicht negierten $x_i=1$
    • Beispiel für einen Minterm: $y = \overline{x}_2 \land \overline{x}_1 \land x_0$
    • Ein Minterm ist ein Monom, in dem alle Variablen vorkommen müssen

Maxterm

  • Gegeben sei eine boolesche Funktion $y = f(x_n, \dots, x_1, x_0)$ und die Literale $\hat{x}_i \in \{\overline{x}_i, x_i\}$.
  • Maxterm: $(\hat{x}_n \lor \dots \lor \hat{x}_2 \lor \hat{x}_1 \lor \hat{x}_0 )$
    • Der Maxterm evaluiert für genau eine bestimmte Konfiguration der Variablen $x_i$ zu 0 und sonst zu 1
    • Genauer gesagt: Der Maxterm evaluiert genau dann zu 0, wenn für alle negierten Variablen $x_i=1$ und alle nicht negierten $x_i=0$
    • Beispiel für einen Maxterm:
      $y = f(x_2, x_1, x_0) = \overline{x}_2 \lor \overline{x}_1 \lor x_0 $

Disjunktive Normalform

  • Eine disjunktive Normalform (DNF) ist eine ODER-Verknüpfung von Mintermen
  • Alle Konfigurationen von Mintermen, in denen $y = f(x_n, \dots, x_1, x_0) = 1$, müssen vorkommen
  • Beispiel:
    x2x1x0yDNF
    0000
    0011(¬x2∧¬x1∧x0)
    0101∨(¬x2∧x1∧¬x0)
    0110
    1001∨(x2∧¬x1∧¬x0)
    1010
    1101∨(x2∧x1∧¬x0)
    1111∨(x2∧x1∧x0)

Disjunktive Normalform (DNF)

Anzahl der Variablen:
Durch Klicken auf die grauen Elemente kann die boolesche Funktion verändert werden

Konjunktive Normalform

  • Eine konjunktive Normalform (KNF) ist eine UND-Verknüpfung von Maxtermen
  • Alle Konfigurationen von Maxtermen, in denen $y = f(x_n, \dots, x_1, x_0) = 0$, müssen vorkommen
  • Beispiel:
    x2x1x0yKNF
    0000(x2∨x1∨x0)
    0011
    0101
    0110∧(x2∨¬x1∨¬x0)
    1001
    1010∧(¬x2∨x1∨¬x0)
    1101
    1111

Konjunktive Normalform (KNF)

Anzahl der Variablen:
Durch Klicken auf die grauen Elemente kann die boolesche Funktion verändert werden

Normalformen der negierten Funktion

  • Teilweise kann es einfacher sein, die Normalform der negierten Funktion zu betrachten
  • Beispiel:
    x2 x1 x0 y DNF y ¬y DNF ¬y
    0 0 0 0 1 (¬x2∧¬x1∧¬x0)
    0 0 1 1 (¬x2∧¬x1∧x0) 0
    0101 ∨(¬x2∧x1∧¬x0) 0
    011 0 1 ∨(¬x2∧x1∧x0)
    100 1 ∨(x2∧¬x1∧¬x0) 0
    1 0 1 0 1 ∨(x2∧¬x1∧x0)
    1 10 1 ∨(x2∧x1∧¬x0) 0
    11 1 1 ∨(x2∧x1∧x0) 0

Umformen der negierten Funktion mit De Morgan

  • Disjunktive Normalform (Beispiel von Folie vorher)
    $\overline{y} = \overline{x}_2 \overline{x}_1 \overline{x}_0 \lor \overline{x}_2 x_1 x_0 \lor x_2 \overline{x}_1 x_0$
    • Mit De Morgans Gesetz (Theorem 14)
      $\begin{align}\lnot \overline{y} &= \lnot (\overline{x}_2 \overline{x}_1 \overline{x}_0 \lor \overline{x}_2 x_1 x_0 \lor x_2 \overline{x}_1 x_0)\\ y &= (x_2 \lor x_1 \lor x_0) \land (x_2 \lor \overline{x}_1 \lor \overline{x}_0) \land (\overline{x}_2 \lor x_1 \lor \overline{x}_0) \end{align}$
  • Konjunktive Normalform (neues Beispiel)
    $\overline{y} = (x_2 \lor \overline{x}_1 \lor x_0 \lor x_3) \land (\overline{x}_2 \lor \overline{x}_1 \lor \overline{x}_0 \lor \overline{x}_3)$
    • Mit De Morgans Gesetz (Theorem 14)
      $\begin{align}\lnot \overline{y} &= \lnot ((x_2 \lor \overline{x}_1 \lor x_0 \lor x_3) \land (\overline{x}_2 \lor \overline{x}_1 \lor \overline{x}_0 \lor \overline{x}_3))\\ y &= \overline{x}_2 x_1 \overline{x}_0 \overline{x}_3 \lor x_2 x_1 x_0 x_3 \end{align}$

Zusammenhang zwischen den Normalformen

  • Umrechnung DNF in KNF
    • Verwenden derjenigen Maxterme $M_i$, die nicht in der Erweiterung der Minterme $m_i$ enthalten sind
    • Beispiel:
      $\mathrm{f}(x_2,x_1,x_0) = \bigvee\limits_{i \in \{1,3,5,6,7\}} m_i = \bigwedge\limits_{i \in \{0,2,4\}} M_i$
  • Umrechnung KNF in DNF
    • Umgekehrtes Vorgehen: Verwenden derjenigen Minterme $m_i$, die nicht in der Erweiterung der Maxterme $M_i$ enthalten sind

Zusammenhang zwischen den Normalformen

Anzahl der Variablen:
Durch Klicken auf die grauen Elemente kann die boolesche Funktion verändert werden

Zusammenhang zwischen den Normalformen

  • Umwandlung der DNF von $\mathrm{f}$ in die DNF von $\lnot \mathrm{f}$
    • Verwenden für $\lnot \mathrm{f}$ diejenigen Minterme $m_i$, die nicht in $\mathrm{f}$ enthalten sind
    • Beispiel:
      $\begin{align}\mathrm{f}(x_2,x_1,x_0) &= \bigvee\limits_{i \in \{1,3,5,6,7\}} m_i \\\Leftrightarrow \lnot\mathrm{f}(x_2,x_1,x_0) &= \bigvee\limits_{i \in \{0,2,4\}} m_i\end{align}$
  • Umwandlung der KNF von $\mathrm{f}$ in die KNF von $\lnot \mathrm{f}$
    • Verwenden für $\lnot \mathrm{f}$ diejenigen Maxterme $M_i$, die nicht in $\mathrm{f}$ enthalten sind
    • Beispiel:
      $\begin{align}\mathrm{f}(x_2,x_1,x_0) &= \bigwedge\limits_{i \in \{0,2,4\}} M_i \\\Leftrightarrow \lnot\mathrm{f}(x_2,x_1,x_0) &= \bigwedge\limits_{i \in \{1,3,5,6,7\}} M_i\end{align}$

Realisierung durch Logikgatter

  • Jede booleschen Funktion $\mathrm{f}=(x_{n-1}, \dots, x_1, x_0)$ der Stelligkeit $n$ lässt sich durch einen Standard-Schaltkreis realisieren, der der DNF bzw. KNF entspricht
  • Im Fall der DNF werden die Minterme durch UND-Gatter mit $n$ Eingängen realisiert
  • Die Erweiterung der Minterme zur DNF erfolgt durch ein ODER-Gatter
  • Beispiel:
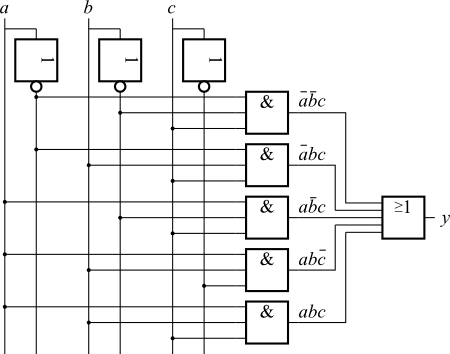
    dnf_logic_gates
    $y = \mathrm{f}(a, b, c) = ab \lor c$
    $a$$b$$c$$y$
    0000
    0011
    0100
    0111
    1000
    1011
    1101
    1111

Realisierung durch Logikgatter

  • Im Fall der KNF werden die Maxterme durch ODER-Gatter mit $n$ Eingängen realisiert
  • Die Erweiterung der Maxterme zur KNF erfolgt durch ein UND-Gatter
  • Beispiel:
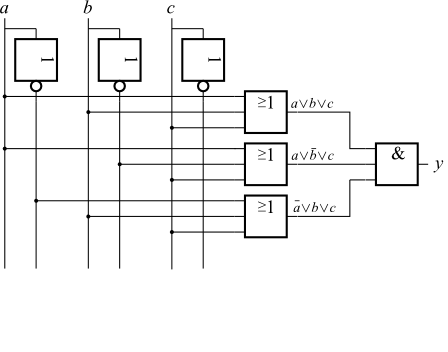
    cnf_logic_gates
    $y = \mathrm{f}(a, b, c) = ab \lor c$
    $a$$b$$c$$y$
    0000
    0011
    0100
    0111
    1000
    1011
    1101
    1111

Quiz

  • Frage: Was ist die DNF für folgende Boolesche Funktion?
    $a$$b$$c$$y$
    0001
    0010
    0101
    0110
    1000
    1010
    1100
    1111
    • Antwort 1: $abc \lor a\bar{b}c \lor \bar{a}\bar{b}\bar{c}$
    • Antwort 2: $\bar{a}\bar{c} \lor abc$
    • Antwort 3: $\bar{a}\bar{b}\bar{c} \lor \bar{a}b\bar{c} \lor abc$

Am Online-Quiz teilnehmen durch Besuch der Webseite:
www.onlineclicker.org

Gibt es Fragen?

questions

Anregungen oder Verbesserungsvorschläge können auch gerne per E-mail an mich gesendet werden: Kontakt


Weitere Vorlesungsfolien

Impressum, Datenschutz,