Steuerungstasten

→ nächste Folie (auch Enter oder Spacebar).
← vorherige Folie
 d  schaltet das Zeichnen auf Folien ein/aus
 p  wechselt zwischen Druck- und Präsentationsansicht
CTRL  +  vergrößert die Folien
CTRL  -  verkleinert die Folien
CTRL  0  setzt die Größenänderung zurück

Das Weiterschalten der Folien kann ebenfalls durch das Klicken auf den rechten bzw. linken Folienrand erfolgen.

Notation

Typ Schriftart Beispiele
Variablen (Skalare) kursiv $a, b, x, y$
Funktionen aufrecht $\mathrm{f}, \mathrm{g}(x), \mathrm{max}(x)$
Vektoren fett, Elemente zeilenweise $\mathbf{a}, \mathbf{b}= \begin{pmatrix}x\\y\end{pmatrix} = (x, y)^\top,$ $\mathbf{B}=(x, y, z)^\top$
Matrizen Schreibmaschine $\mathtt{A}, \mathtt{B}= \begin{bmatrix}a & b\\c & d\end{bmatrix}$
Mengen kalligrafisch $\mathcal{A}, B=\{a, b\}, b \in \mathcal{B}$
Zahlenbereiche, Koordinatenräume doppelt gestrichen $\mathbb{N}, \mathbb{Z}, \mathbb{R}^2, \mathbb{R}^3$

Inhalt

  • Arithmetik Schaltungen
    • Addition
    • Inkrement
    • Subtraktion
    • Multiplikation
  • Arithmetisch-logische Einheit (ALU)

Addition

  • Zur Entwicklung einer Schaltung für die Addition kann sich an der schriftlichen Addition orientiert werden:
    $ \begin{aligned} \begin{aligned} 13& \\ +\ 5& \\ \hline =18&\\ \end{aligned} && \begin{aligned} 1101&&(13)\\ +0101&&(05)\\ \hline =10010&&(18)\\ \end{aligned} \end{aligned} $
  • Die Addition wird Bit-weise von rechts nach links durchgeführt (angefangen beim niederwertigsten Bit)
  • Es kann zu einem Übertrag (Carry) kommen, der beim nächsten Bit berücksichtigt werden muss

Halbaddierer

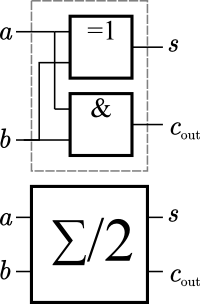
half_adder_details
Halbaddierer
  • Beim niederwertigsten Bit müssen nur alle Kombinationen der zwei Summanden $a$ und $b$ betrachtet werden (4 Fälle)
  • Frage: Wie lautet jeweils das Ergebnis der Addition $s$ und der Übertrag $c_{\text{out}}$ (Carry-out)?
    $a$$b$$s$$c_{\text{out}}$
    0000
    0110
    1010
    1101
  • Damit ergibt sich:
    • $s = \overline{a}b \lor a\overline{b} = a \nleftrightarrow b$
    • $c_{\text{out}} = ab$
  • Die Realisierung mit Logikgattern wird Halbaddierer  genannt und erhält ein eigenes Symbol (siehe rechts)

Volladdierer

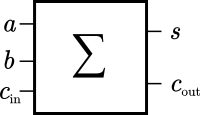
full_adder_details2
Volladdierer
  • Bei den nachfolgenden Bits muss nun ebenfalls der Übertrag $c_{\text{in}}$ der vorangegangen Bit-weisen Addition berücksichtigt werden (Carry-in)
    $a$$b$$c_{\text{in}}$$s$$c_{\text{out}}$
    00000
    00110
    01010
    01101
    10010
    10101
    11001
    11111
  • Damit ergibt sich:
    • $s = \overline{a}\overline{b}c_{\text{in}} \lor \overline{a}b\overline{c}_{\text{in}} \lor a\overline{b}\overline{c}_{\text{in}} \lor abc_{\text{in}}$
    • $c_{\text{out}} = \overline{a}bc_{\text{in}} \lor a\overline{b}c_{\text{in}} \lor ab\overline{c}_{\text{in}} \lor abc_{\text{in}}$

Volladdierer

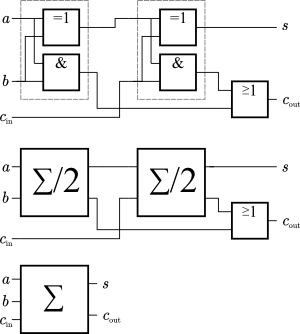
full_adder_details
Volladdierer
  • Durch Umformung der booleschen Ausdrücke ergibt sich:
    $\begin{align} s&= \overline{a}\overline{b}c_{\text{in}} \lor \overline{a}b\overline{c}_{\text{in}} \lor a\overline{b}\overline{c}_{\text{in}} \lor abc_{\text{in}}\\ &\stackrel{\small (6)}{=} \left(\overline{a}\overline{b}c_{\text{in}} \lor abc_{\text{in}}\right) \lor \left(\overline{a}b\overline{c}_{\text{in}} \lor a\overline{b}\overline{c}_{\text{in}} \right)\\ &\stackrel{\small (8)}{=} \left(\left(\overline{a}\overline{b} \lor ab\right) c_{\text{in}} \right) \lor \left(\left(\overline{a}b \lor a\overline{b}\right)\overline{c}_{\text{in}} \right)\\ &= \left( \left( a \leftrightarrow b \right)c_{\text{in}} \right) \lor \left(\left(a \nleftrightarrow b \right) \overline{c}_{\text{in}}\right)\\ &= \left(\left( \overline{a \nleftrightarrow b} \right) c_{\text{in}} \right) \lor \left(\left(a \nleftrightarrow b \right)\overline{c}_{\text{in}} \right)\\ &= \left(a \nleftrightarrow b \right)\nleftrightarrow c_{\text{in}} \\ \end{align}$
    $\begin{align} c_{\text{out}}&= \left(\overline{a}bc_{\text{in}} \lor a\overline{b}c_{\text{in}}\right) \lor \left(ab\overline{c}_{\text{in}} \lor abc_{\text{in}}\right)\\ &\stackrel{\small (8)}{=} \left( \left(\overline{a}b \lor a\overline{b}\right)c_{\text{in}} \right) \lor \left(ab\left(\overline{c}_{\text{in}} \lor c_{\text{in}}\right)\right)\\ &\stackrel{\small (5)}{=} \left(a \nleftrightarrow b\right)c_{\text{in}} \lor ab \end{align}$

Carry-Ripple-Addierer

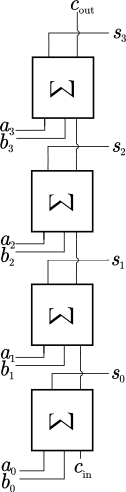
adder_carry_ripple
  • Ein Addierwerk für Binärzahlen der Stelligkeit $n$ kann mit $n$ Volladdierern realisiert werden
  • Jeder Ein-Bit-Addierer ist für eine Ziffer $s_i$ der Summe verantwortlich
  • Der $c_{\text{out}}$-Ausgang wird jeweils mit dem $c_{\text{in}}$ des nächsten Ein-Bit-Addierers verbunden
  • Die Laufzeit ist linear in der Anzahl der Stellen, da jeder Ein-Bit-Addierer zunächst auf den Übertrag seines Vorgängers warten muss (d.h. ein 8-Bit-Addierwerk braucht doppelt so lange, wie ein 4-Bit-Addierwerk)
  • Die Behandlung des Übertrags (Carry) limitiert die Laufzeit. Das Carry "rieselt" (engl. "ripple") langsam durch die Schaltung.

Carry-Look-Ahead-Addierer

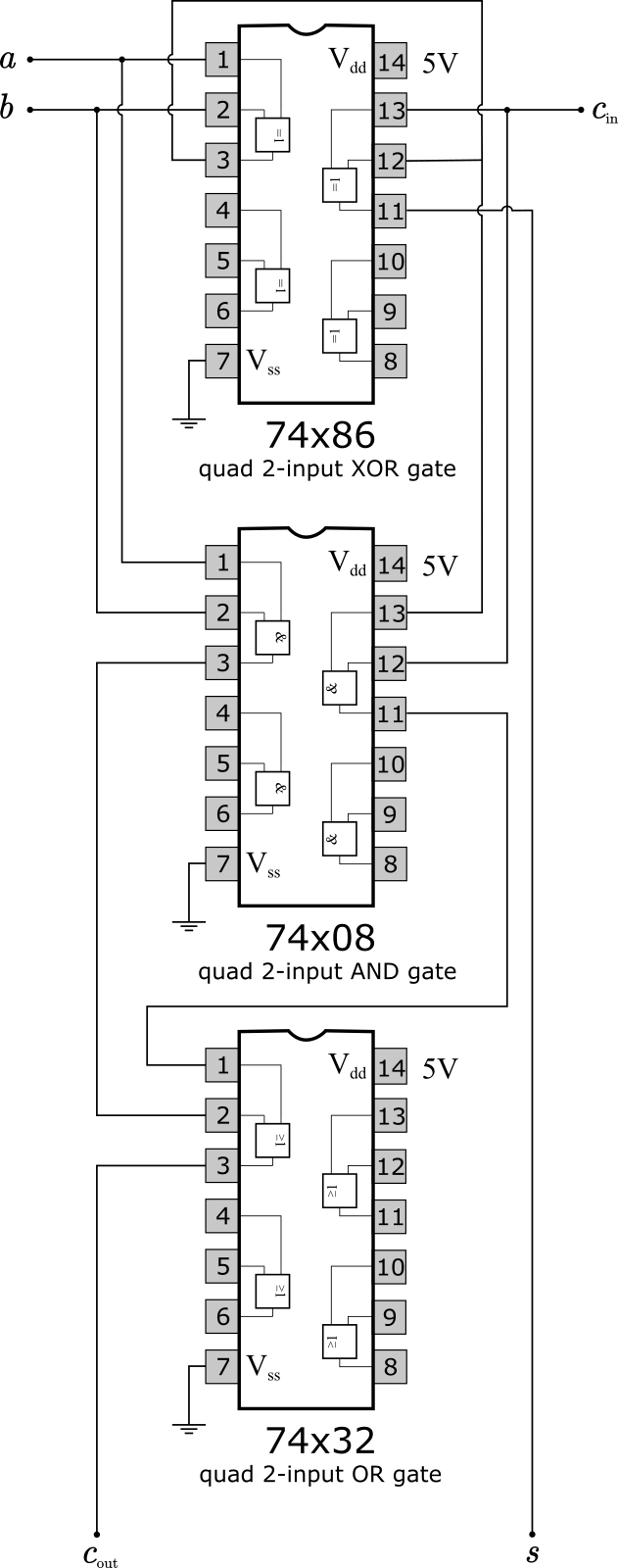
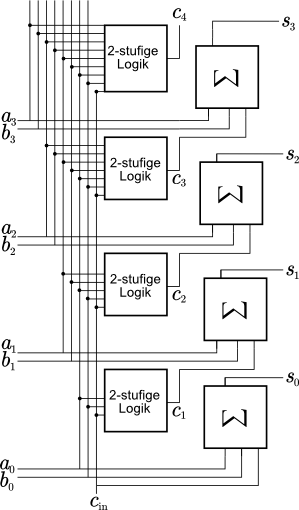
adder_carry_lookahead
  • Die Idee des Carry-Look-Ahead-Addierers ist, die Carry-Bits für alle Ein-Bit-Addierer durch eine separate Logikschaltung zu erzeugen
  • Wie in den vorangegangenen Kapiteln gezeigt wurde, kann jede boolesche Funktion als zweistufige Logik realisiert werden
  • Beim Carry-Look-Ahead-Addierer können alle Ein-Bit-Addierer parallel arbeiten und liefern zeitgleich ihr Ergebnis
  • Allerdings steigt mit jeder Ziffer der Aufwand für die Realisierung der Übertragsberechnung mittels zweistufiger Logik, da mit jeder Ziffer zwei Eingänge hinzukommen

Carry-Look-Ahead-Addierer

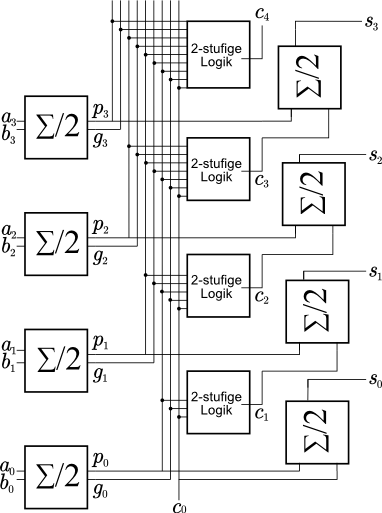
adder_carry_lookahead_half
  • Um die Anzahl der Gatter innerhalb der 2-stufigen Logik zu reduzieren, wird der boolesche Ausdruck zur Berechnung des Übertrags beim Volladdierer betrachtet
  • Bei gegebenem Übertrag $c_i$ des vorherigen Ein-Bit-Addierers berechnet sich $c_{i+1}$
    $\begin{align} c_{i+1}&= \underbrace{\left(a_i \nleftrightarrow b_i\right)}_{p_i}c_i \lor \underbrace{a_i b_i}_{g_i} \end{align}$
  • Dabei sind $p_i$ und $g_i$ gerade die Ausgänge eines entsprechenden Halbaddierers
  • Um diese Werte bei der Berechnung des Übertrags abzugreifen, werden die Volladdierer in zwei Halbaddierer aufgespaltet

Carry-Look-Ahead-Addierer

  • Durch rekursive Anwendung des Ausdrucks zur Berechnung des Übertrags
    $\begin{align} c_{i+1}&= \underbrace{\left(a_i \nleftrightarrow b_i\right)}_{p_i}c_i \lor \underbrace{a_i b_i}_{g_i} \end{align}$
    kann die benötigte 2-stufige Logik ausgerechnet werden:
    $\begin{align} c_{1}&= p_0 c_0 \lor g_0\\ c_{2}&= p_1 c_1 \lor g_1\\ &= p_1 (p_0 c_0 \lor g_0) \lor g_1\\ &= p_1 p_0 c_0 \lor p_1 g_0 \lor g_1\\ c_{3}&= p_2 c_2 \lor g_2\\ &=p_2 (p_1 p_0 c_0 \lor p_1 g_0 \lor g_1) \lor g_2\\ &= p_2 p_1 p_0 c_0 \lor p_2 p_1 g_0 \lor p_2 g_1 \lor g_2\\ c_{4}&= p_3 c_3 \lor g_3\\ &= p_3 (p_2 p_1 p_0 c_0 \lor p_2 p_1 g_0 \lor p_2 g_1 \lor g_2) \lor g_3\\ &= p_3 p_2 p_1 p_0 c_0 \lor p_3 p_2 p_1 g_0 \lor p_3 p_2 g_1 \lor p_3 g_2 \lor g_3\\ \end{align}$

Inkrement

  • Das Inkrementieren einer Zahl (a=a+1 bzw. kurz a++) ist eine sehr häufige arithmetische Operation
  • Z.B. muss nach jeder Befehlsausführung der Programmzähler erhöht werden, oder, beim sequentiellen Lesen aus dem Speicher, der Adresszähler
  • Ein weiteres Beispiel sind Schleifen, bei denen das Inkrementieren der Zählvariablen um 1 eine typische Operation ist: 
    for(int a = 0; a < 10; a++) {
  doSomething(a);
}

Inkrement

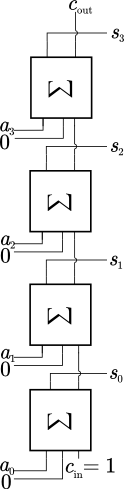
adder_increment
  • Ein $n$-stelliger Inkrementierer kann mit einem $n$-stelligen Addiererwerk realisiert werden, indem alle $b_i$ gleich $0$ und der Übertrag am Eingang des niederwertigsten Bits $c_{\text{in}}$ gleich $1$ gesetzt wird
  • Die Abbildung rechts zeigt dies für den Carry-Ripple-Addierer
  • Durch feste Verdrahtung einiger Variablen kann die Schaltung vereinfacht werden, z.B. können beim Carry-Ripple-Addierer die Volladdierer durch entsprechend beschaltete Halbaddierer ersetzt werden
    full_adder_details_b0

Subtraktion

  • Die Subtraktion zweier Zahlen $y= a-b$ kann auf die Addition zurückgeführt werden $y = a + (-b)$
  • Dazu werden die Zahlen im Zweierkomplement dargestellt
  • Zur Wiederholung: Beim Zweierkomplement werden die negativen Zahlen durch das bitweise Komplement und einer zusätzlichen Addition von 1 gebildet
    • Beispiel:
      $(-6)_{10} \hat{=} \ 1001 + 1 = 1010$
  • Subtraktion mit dem Zweierkomplement:
    $ \begin{aligned} \begin{aligned} 5& \\ +-6& \\ \hline =-1&\\ \end{aligned} && \begin{aligned} 0101&&(5)\\ +1010&&(-6)\\ \hline =1111&&(-1)\\ \end{aligned} \end{aligned}$

Subtraktion

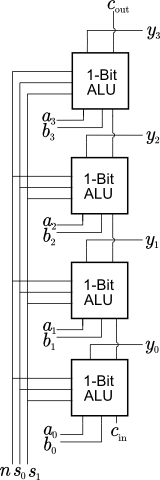
sub_carry_ripple
  • Ein $n$-stelliger Subtrahierer kann mit einem $n$-stelligen Addiererwerk realisiert werden, indem eine zusätzliche Logik zu Berechnung des Zweierkomplements hinzugefügt wird
  • Die Abbildung rechts zeigt dies am Beispiel des Carry-Ripple-Addierers
  • Der Eingang $n$ wählt aus, ob $b$ negiert werden soll, und der Ausgang $v$ zeigt an, ob ein Überlauf (Overflow) aufgetreten ist

Multiplikation

  • Zur Entwicklung einer Schaltung für die Multiplikation wird zunächst die schriftliche Multiplikation (wie aus der Schule bekannt) betrachtet:
    $\begin{aligned} 25 \cdot 13& \\ \hline 75& \\ +25\ \ & \\ \hline = 325&\\ \end{aligned}$
    $\begin{aligned} 11001 \cdot 1101& \\ \hline 11001& \\ 00000\hspace{1.2ex}\\ 11001\hspace{2.4ex}& \\ + 11001\hspace{3.6ex}& \\\hline = 101000101&\\ \end{aligned}$
  • Es ist zu erkennen, dass die Multiplikation von Binärzahlen durch eine Verschiebung und Addition realisiert werden kann

Matrixmultiplizierer

  • Eine Schaltung, die das schriftliche Multiplizieren nachbildet, ist der Matrixmultiplizierer
  • Gegeben sei Multiplikator $a = a_{n-1}\dots a_1 a_0$ und Multiplikand $b = b_{n-1}\dots b_1 b_0$ mit Stelligkeit $n$
  • Die Anordnung der Bits beim schriftlichen Multiplizieren kann als $n \times (2n-1)$ Matrix dargestellt werden
    $\begin{bmatrix}0 & \dots & 0 & a_{n-1} b_0 & a_{n-2}b_0 & \dots & a_{2}b_0 & a_{1}b_0 & a_{0}b_0 \\ 0 & \dots & a_{n-1}b_1 & a_{n-2}b_1 & a_{n-3}b_1 & \dots & a_{1}b_1 & a_{0}b_1 &0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots &\vdots \\ a_{n-1}b_{n-1} & \dots & a_{1}b_{n-1} & a_{0}b_{n-1} & 0 & \dots & 0 & 0 & 0 \\ \end{bmatrix}$
  • Diese Matrixstruktur findet sich auch in der entsprechenden Logikschaltung wieder
    • Die Elemente der Matrix werden durch UND-Verknüpfungen $a_j\land b_i$ berechnet
    • Jede Spaltensumme durch ein Addierwerk (benötigt maximal $n-1$ Volladdierer)

4-Bit-Matrixmultiplizierer

multiply

Multiplizierer

  • Die vorgestellte Realisierung eines Multiplizierers hat das gleiche Problem, wie der Carry-Ripple-Addierer: Das Warten auf den Übertrag limitiert die Laufzeit
  • Analog, wie beim Addierer, können Schaltungen entworfen werden, die mehr Logikgatter für die Berechnung des Übertrags bereitstellen und damit die Laufzeit reduzieren

Arithmetisch-logische Einheit (ALU)

  • Die arithmetisch-logische Einheit (engl. arithmetic logic unit, ALU) dient zur Realisierung der Elementaroperationen eines Rechners
  • Dazu gehören
    • Arithmetische Operationen: Addition, Subtraktion, Multiplikation, ...
    • Logische Operationen: Bitweise UND-Verknüpfung, ODER-Verknüpfung, Prüfen auf Gleichheit, ....

Arithmetisch-logische Einheit (ALU)

  • In einer ALU werden zwei Eingabewerte $a$ und $b$ zu einem Ergebniswert $y$ verknüpft
  • Diese Werte stehen in Registern zur Verfügung (Registerbreite kann 8, 16, 32, 64 Bits sein)
  • Der "Mode" selektiert, welche Funktion die ALU ausführen soll
  • Im "Flag" wird der Status der ALU angezeigt, z.B. wenn ein Überlauf stattgefunden hat
  • Zur schematischen Darstellung hat sich folgendes Symbol etabliert:
    alu

Arithmetisch-logische Einheit (ALU)

  • Flag-Register (Statusregister)
    • Übertrag $c$ (Carry flag): Übertrag ist aufgetreten
    • Überlauf $v$ (Overflow flag): Ergebnis passt nicht ins $y$-Register
    • Null $z$ (Zero flag): Ergebnis is Null
    • Negativ $n$ (Negation flag): Ergebnis ist negativ
    • ...
  • Der Mode-Eingang wählt die auszuführende Operation aus
    alu_mode

Beispiel für eine ALU

sub_carry_ripple
4-Bit-ALU
  • Zur Realisierug einer einfachen ALU soll diese aus mehreren
    1-Bit-ALUs zusammengesetzt werden
  • Wie bereits von den Addierwerken bekannt, muss dabei die Carry-Information an den Nachfolger weitergegeben werden
  • Insgesamt soll die hier gezeigte beispielhafte ALU acht verschiedene Operationen ausführen:
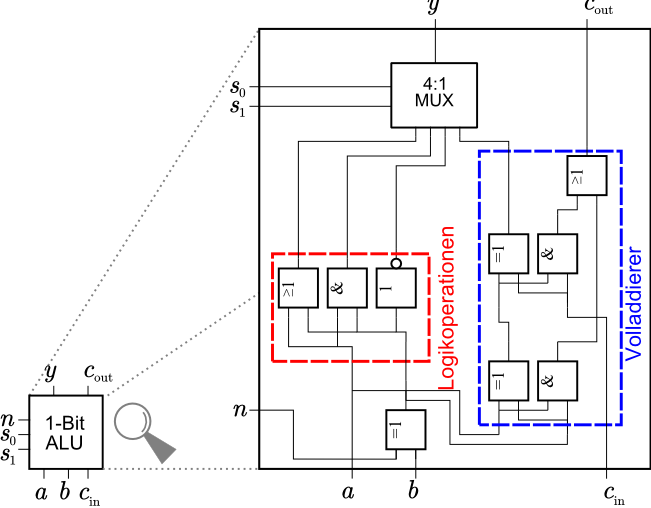
    $s_1$$s_0$$n$$y$
    000$a \lor b$
    001$a \lor \overline{b}$
    010$a \land b$
    011$a \land \overline{b}$
    100$\overline{b}$
    101$b$
    110$a + b$
    111$a + \overline{b}$

1-Bit ALU

alu_1bit

Gibt es Fragen?

questions

Anregungen oder Verbesserungsvorschläge können auch gerne per E-mail an mich gesendet werden: Kontakt


Weitere Vorlesungsfolien

Impressum, Datenschutz,