MathTL::LaurentPolynomial< R > Class Template Reference

#include <laurent_polynomial.h>

Inheritance diagram for MathTL::LaurentPolynomial< R >:

List of all members.

Public Types
typedef InfiniteVector< R, int > ::const_iterator	const_iterator
typedef InfiniteVector< R, int > ::const_reverse_iterator	const_reverse_iterator
Public Member Functions
	LaurentPolynomial ()
	LaurentPolynomial (const LaurentPolynomial< R > &p)
	LaurentPolynomial (const R c)
	LaurentPolynomial (const Polynomial< R > &p)
virtual	~LaurentPolynomial ()
LaurentPolynomial< R > &	operator= (const LaurentPolynomial< R > &p)
LaurentPolynomial< R > &	operator= (const R c)
unsigned int	degree () const
R	get_coefficient (const int k) const
void	set_coefficient (const int k, const R coeff)
const_iterator	begin () const
const_iterator	end () const
const_reverse_iterator	rbegin () const
const_reverse_iterator	rend () const
R	value (const R x) const
R	value (const Point< 1 > &p, const unsigned int component=0) const
void	vector_value (const Point< 1 > &p, Vector< R > &values) const
void	add (const LaurentPolynomial< R > &p)
void	add (const R s, const LaurentPolynomial< R > &p)
void	sadd (const R s, const LaurentPolynomial< R > &p)
LaurentPolynomial< R > &	operator+= (const LaurentPolynomial< R > &p)
LaurentPolynomial< R >	operator+ (const LaurentPolynomial< R > &p) const
void	subtract (const LaurentPolynomial< R > &p)
LaurentPolynomial< R > &	operator-= (const LaurentPolynomial< R > &p)
LaurentPolynomial< R >	operator- () const
LaurentPolynomial< R >	operator- (const LaurentPolynomial< R > &p) const
LaurentPolynomial< R > &	operator*= (const R c)
LaurentPolynomial< R >	operator* (const R c) const
void	multiply (const LaurentPolynomial< R > &p)
LaurentPolynomial< R > &	operator*= (const LaurentPolynomial< R > &p)
LaurentPolynomial< R >	power (const unsigned int k) const
void	divide (const LaurentPolynomial< R > &q, LaurentPolynomial< R > &p) const
void	divide (const LaurentPolynomial< R > &q, LaurentPolynomial< R > &p, LaurentPolynomial< R > &r) const

---

Detailed Description

template<class R>
class MathTL::LaurentPolynomial< R >

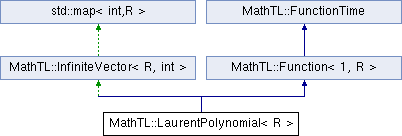
A template class for general univariate Laurent polynomials, i.e., expressions of the form a(z)={k Z} a_k z^k The a_k and z are elements of a (number) ring R.

Examples: R= R or C

---

Member Typedef Documentation

template<class R>

typedef InfiniteVector<R,int>::const_iterator MathTL::LaurentPolynomial< R >::const_iterator

const_iterator scanning the nontrivial coefficients

template<class R>

typedef InfiniteVector<R,int>::const_reverse_iterator MathTL::LaurentPolynomial< R >::const_reverse_iterator

const_reverse_iterator scanning the nontrivial coefficients

---

Constructor & Destructor Documentation

template<class R >

MathTL::LaurentPolynomial< R >::LaurentPolynomial

(

)

default constructor, yields zero (Laurent) polynomial

template<class R>

MathTL::LaurentPolynomial< R >::LaurentPolynomial

(

const LaurentPolynomial< R > &

p

)

copy constructor

template<class R>

MathTL::LaurentPolynomial< R >::LaurentPolynomial

(

const R

c

)

[explicit]

constructor from a constant

template<class R>

MathTL::LaurentPolynomial< R >::LaurentPolynomial

(

const Polynomial< R > &

p

)

[explicit]

constructor from a polynomial

template<class R >

MathTL::LaurentPolynomial< R >::~LaurentPolynomial

(

)

[virtual]

virtual destructor

---

Member Function Documentation

template<class R>

void MathTL::LaurentPolynomial< R >::add

(

const LaurentPolynomial< R > &

p

)

[inline]

pointwise sum of two Laurent polynomials *this += p

template<class R>

void MathTL::LaurentPolynomial< R >::add	(	const R	s,
		const LaurentPolynomial< R > &	p
	)		[inline]

pointwise weighted sum of two Laurent polynomials *this += s*p

template<class R >

LaurentPolynomial< R >::const_iterator MathTL::LaurentPolynomial< R >::begin

(

)

const [inline]

const_iterator pointing to the first nontrivial coefficient

Reimplemented from MathTL::InfiniteVector< R, int >.

template<class R >

unsigned int MathTL::LaurentPolynomial< R >::degree

(

)

const [inline]

(Euclidean) degree of a Laurent polynomial

template<class R>

void MathTL::LaurentPolynomial< R >::divide	(	const LaurentPolynomial< R > &	q,
		LaurentPolynomial< R > &	p
	)		const

division with remainder by another Laurent polynomial q: *this = p * q + r

template<class R>

void MathTL::LaurentPolynomial< R >::divide	(	const LaurentPolynomial< R > &	q,
		LaurentPolynomial< R > &	p,
		LaurentPolynomial< R > &	r
	)		const

division with remainder by another Laurent polynomial q: *this = p * q + r

template<class R >

LaurentPolynomial< R >::const_iterator MathTL::LaurentPolynomial< R >::end

(

)

const [inline]

const_iterator pointing to one behind the last nontrivial coefficient

Reimplemented from MathTL::InfiniteVector< R, int >.

template<class R >

R MathTL::LaurentPolynomial< R >::get_coefficient

(

const int

k

)

const [inline]

(Polynomial-like) read-only access to single coefficients

template<class R>

void MathTL::LaurentPolynomial< R >::multiply

(

const LaurentPolynomial< R > &

p

)

pointwise multiplication with another Laurent polynomial

template<class R>

LaurentPolynomial<R> MathTL::LaurentPolynomial< R >::operator*

(

const R

c

)

const

multiplication with a real number from the right (don't use this extensively, since one copy has to be made!)

template<class R>

LaurentPolynomial< R > & MathTL::LaurentPolynomial< R >::operator*=

(

const R

c

)

[inline]

multiplication with a real number

Reimplemented from MathTL::InfiniteVector< R, int >.

template<class R>

LaurentPolynomial< R > & MathTL::LaurentPolynomial< R >::operator*=

(

const LaurentPolynomial< R > &

p

)

[inline]

pointwise multiplication with another Laurent polynomial

template<class R>

LaurentPolynomial< R > MathTL::LaurentPolynomial< R >::operator+

(

const LaurentPolynomial< R > &

p

)

const [inline]

pointwise sum of two Laurent polynomials (don't use this extensively, since one copy has to be made!)

template<class R>

LaurentPolynomial< R > & MathTL::LaurentPolynomial< R >::operator+=

(

const LaurentPolynomial< R > &

p

)

[inline]

pointwise sum of two Laurent polynomials

template<class R >

LaurentPolynomial< R > MathTL::LaurentPolynomial< R >::operator-

(

)

const [inline]

sign (makes a copy of *this)

template<class R>

LaurentPolynomial< R > MathTL::LaurentPolynomial< R >::operator-

(

const LaurentPolynomial< R > &

p

)

const [inline]

pointwise difference of two Laurent polynomials (don't use this extensively, since one copy has to be made!)

template<class R>

LaurentPolynomial< R > & MathTL::LaurentPolynomial< R >::operator-=

(

const LaurentPolynomial< R > &

p

)

[inline]

pointwise difference of two Laurent polynomials

template<class R>

LaurentPolynomial< R > & MathTL::LaurentPolynomial< R >::operator=

(

const LaurentPolynomial< R > &

p

)

assignment of another Laurent polynomial

template<class R>

LaurentPolynomial< R > & MathTL::LaurentPolynomial< R >::operator=

(

const R

c

)

assignment of a constant

template<class R >

LaurentPolynomial< R > MathTL::LaurentPolynomial< R >::power

(

const unsigned int

k

)

const

raise the Laurent polynomial to some power

template<class R >

LaurentPolynomial< R >::const_reverse_iterator MathTL::LaurentPolynomial< R >::rbegin

(

)

const [inline]

const_reverse_iterator pointing to the last nontrivial coefficient

Reimplemented from MathTL::InfiniteVector< R, int >.

template<class R >

LaurentPolynomial< R >::const_reverse_iterator MathTL::LaurentPolynomial< R >::rend

(

)

const [inline]

const_reverse_iterator pointing to one before the first nontrivial coefficient

Reimplemented from MathTL::InfiniteVector< R, int >.

template<class R>

void MathTL::LaurentPolynomial< R >::sadd	(	const R	s,
		const LaurentPolynomial< R > &	p
	)		[inline]

pointwise weighted sum of two Laurent polynomials *this = s*(*this) + p

template<class R>

void MathTL::LaurentPolynomial< R >::set_coefficient	(	const int	k,
		const R	coeff
	)		[inline]

(Polynomial-like) write access to single coefficients

template<class R>

void MathTL::LaurentPolynomial< R >::subtract

(

const LaurentPolynomial< R > &

p

)

[inline]

pointwise difference of two Laurent polynomials *this -= p

template<class R>

R MathTL::LaurentPolynomial< R >::value

(

const R

x

)

const

evaluate the Laurent polynomial (Horner scheme)

template<class R>

R MathTL::LaurentPolynomial< R >::value	(	const Point< 1 > &	p,
		const unsigned int	component = 0
	)		const [inline]

evaluate the Laurent polynomial (Horner scheme) (calls the above value(const R))

template<class R>

void MathTL::LaurentPolynomial< R >::vector_value	(	const Point< 1 > &	p,
		Vector< R > &	values
	)		const [inline]

evaluate the Laurent polynomial (Horner scheme) (calls the above value(const R))

---

The documentation for this class was generated from the following files:

• algebra/laurent_polynomial.h
• algebra/laurent_polynomial.cpp