Poncelet's Theorem

(There is also a german version of this page.)

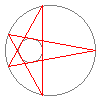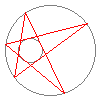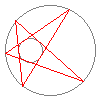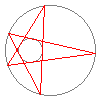This nice animation of Poncelet's theorem is due to W. Barth.

What is it about?

Poncelet's theorem is a famous porism -- in fact it may be viewed as a »prototype« of all such theorems. It is about two conics in the (projective) plane that do not touch each other -- in the animation these are the two circles. Here is the statement of the theorem:

If there is an n-gon that is inscribed into one of the conics and circumscribed on the other conic, then there are infinitely many such n-gons.

More precisely, there is then in fact such an n-gon through any point on the conics.

What has the theorem got do to with the animation?

Well, it is Poncelet's theorem which makes such an animation possible in the first place. This is because in practice the theorem means that an n-gon that is inscribed/circumscribed between two conics may be »continuously deformed«. You can see this in the pentagon that is inscribed into the outer conic and circumscribed on the inner conic: Poncelet's theorem guarantees that we may »rotate« the pentagon without breaking it apart.

Where can I learn more
about Poncelet's theorem?

Griffiths and Harris have given a modern proof of Poncelet's theorem in their paper

• Ph. Griffiths, J. Harris:
  A Poncelet theorem in space.
  Comment. Math. Helvetici 52, 145-160 (1977)

The proof takes place in algebraic geometry, and it reveals that an elliptic curve is at work behind the scenes here.

A quick internet search provides interesting sites, too -- for instance the nice Staatsexamensarbeit by Ulrike Herr.

If you now got interested in further theorems of this kind, you will find a collection of them in the paper

• Th. Bauer, W. Barth:
  Poncelet theorems.
  Exposition. Math. 14, 125-144 (1996)

along with modern proofs and hints to the literature. (Also, you learn there that almost always an elliptic curve is working behind the scenes -- it is responsible for the porism to work.)