Der Satz von Poncelet

(There is also an english version of this page.)

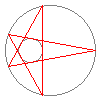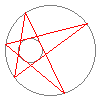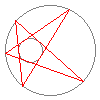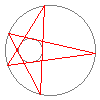Diese schöne Visualisierung des Satzes von Poncelet stammt von W. Barth.

Worum geht es?

Der Satz von Poncelet ist ein berühmter Schließungssatz -- tatsächlich kann man ihn durchaus als »Prototyp« aller geometrischen Schließungsätze betrachen. Er handelt von zwei Kegelschnitten in der (projektiven) Ebene, die sich nicht berühren -- in der obigen Animation sind dies die beiden Kreise. Hier ist die Aussage des Satzes:

Falls es ein n-Eck gibt, das dem einen Kegelschnitt einbeschrieben und dem anderen Kegelschnitt umbeschrieben ist, so gibt es unendlich viele solcher n-Ecke.

Genauer kann man sogar sagen, daß es durch jeden Punkt auf den Kegelschnitten ein derartiges n-Eck gibt.

Was hat dies mit der Animation zu tun?

Nun, die Animation wird durch den Satz von Poncelet überhaupt erst möglich. Denn in der Praxis bedeutet der Satz, daß man ein n-Eck, das zwei Kegelschnitten ein- bzw. umbeschrieben ist, »stetig deformieren« kann. Sie sehen dies oben am Beispiel eines Fünfecks: Es ist dem inneren Kreis umbeschrieben und dem äußeren Kreis einbeschrieben. Der Satz von Poncelet garantiert, daß wir das Fünfeck »rotieren« lassen können, ohne daß es auseinanderbricht.

Wo kann man
mehr über den Satz von Poncelet erfahren?

Griffiths und Harris haben in der Arbeit

• Ph. Griffiths, J. Harris:
  A Poncelet theorem in space.
  Comment. Math. Helvetici 52, 145-160 (1977)

einen modernen Beweis für den Satz von Poncelet gegeben. Der Beweis wird im Rahmen der algebraischen Geometrie geführt und bringt den Kern der Sache ans Licht: Hinter dem Schließungsprozess steckt eine elliptische Kurve.

Auch eine Suche im Internet liefert einige interessante Fundstellen, z.B. eine schöne Staatsexamensarbeit von Ulrike Herr.

Wenn Sie an weiteren Schließungssätzen interessiert sind, so finden Sie in der Arbeit

• Th. Bauer, W. Barth:
  Poncelet theorems.
  Exposition. Math. 14, 125-144 (1996)

eine Zusammenstellung von Schließungssätzen mit modernen Beweisen und Angaben zu weiterer Literatur. (Außerdem erfahren Sie dort, dass fast immer eine elliptische Kurve hinter den Kulissen arbeitet und für den Schließungsprozess letztlich verantwortlich ist.)