Wavelet and Multiscale Library
Demo page
This page is designed for tutors and lecturers. Here, you find a broad selection of examples, demo programs, as well as illustrating images that can be shown readily in lectures or presentations. You may navigate this page by using the directory on the left.
Wavelets
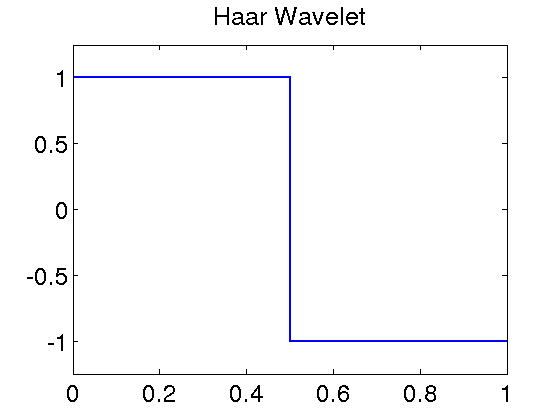
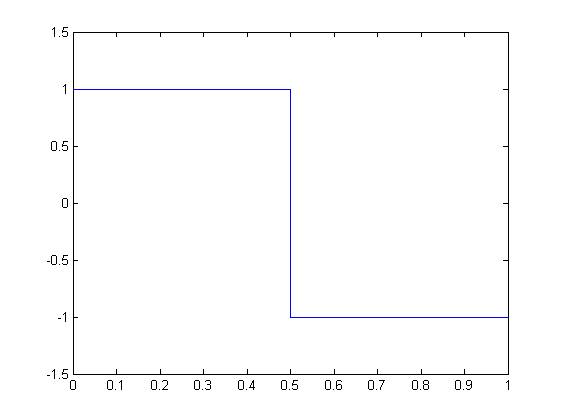
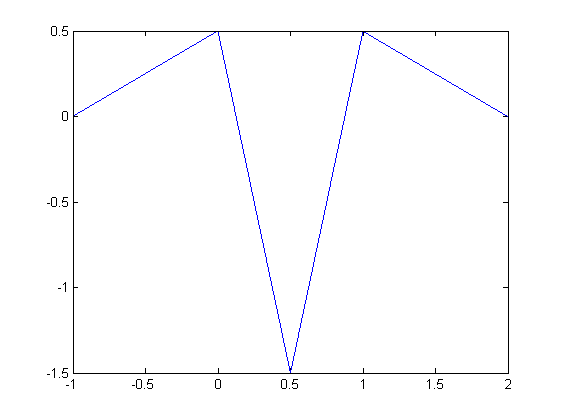
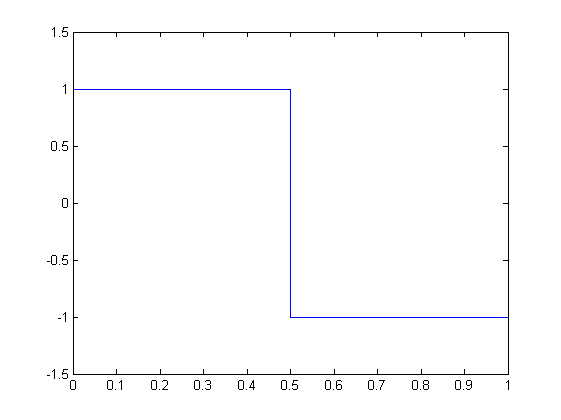
Haar Wavelet
The Haar wavelet is a piecewise constant function whose dyadic dilates and integer translates form an orthonormal basis in L2 over the real line.
A. Haar, Zur Theorie der orthogonalen Funktionensysteme, Math. Ann. 69 (1910), 331-371.
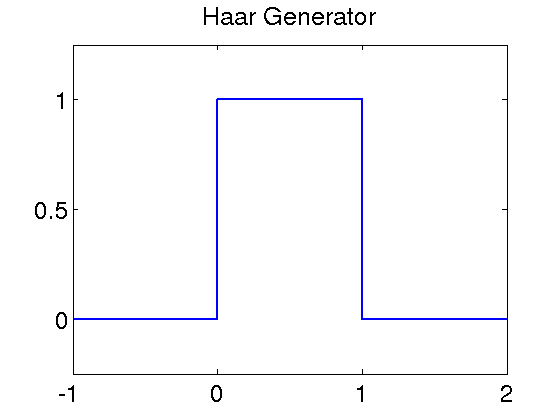
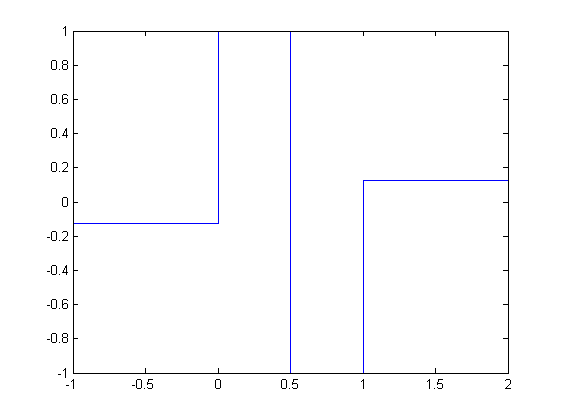
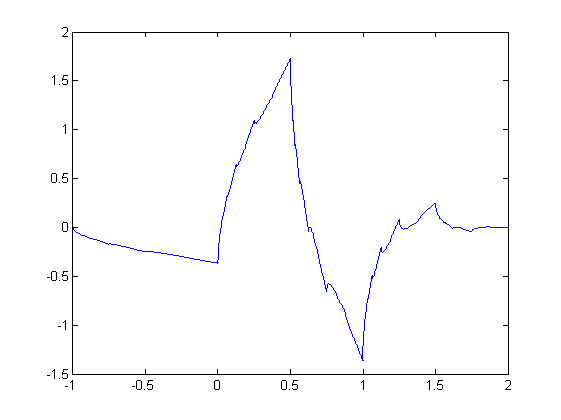
Refinable functions via Subdivision
A refinable function is a function that solves a refinement equation with respect to a given mask. If a refinable function generates a multiresolution analysis in L2, it can be used to construct a wavelet basis for this space; in this case it is called scaling function.
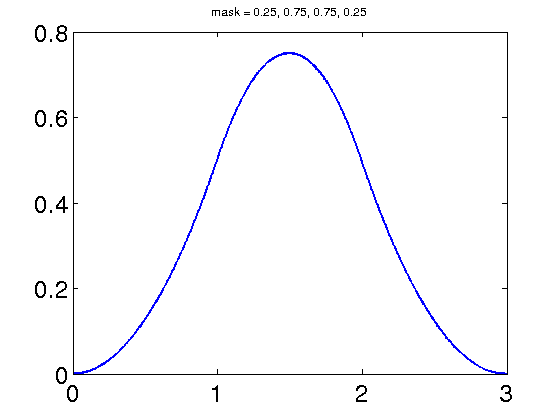
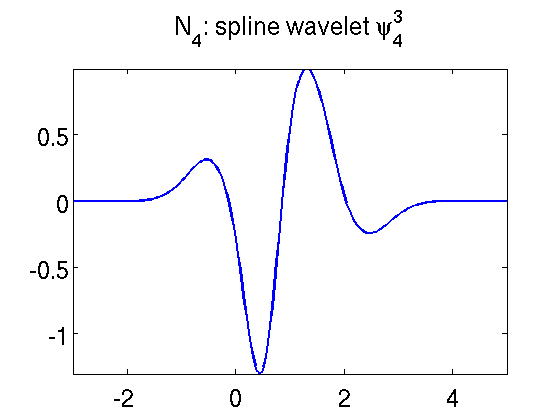
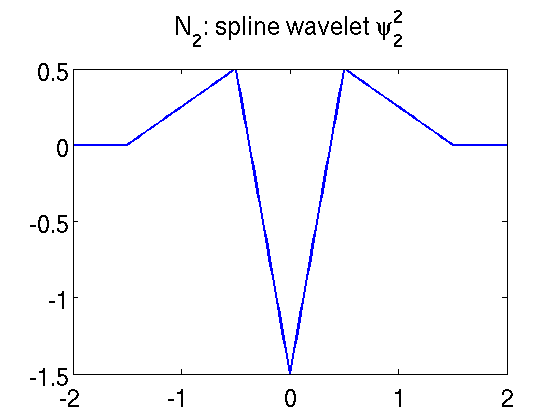
Spline Wavelets
Spline wavelets are generated from cardinal B-spline scaling functions.
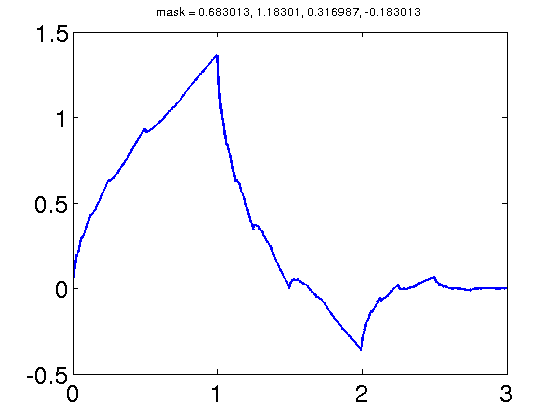
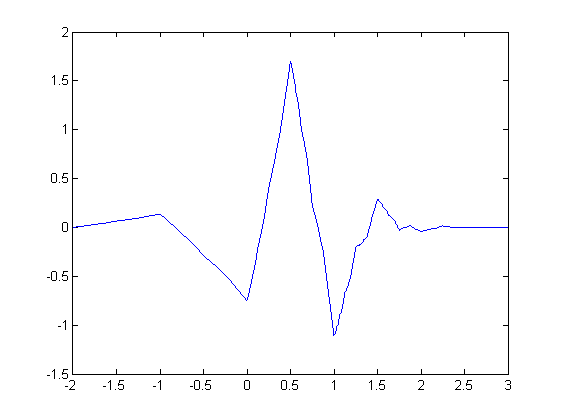
Cohen/Daubechies/Feauveau Wavelets
 (d=1,dt=1) |
 (d=1,dt=3) |
 (d=2,dt=2) |
[a,astart]=N_mask(d);[at,atstart]=CDF_mask(d,dt);plot_wavelet(a,astart,at,atstart,10)
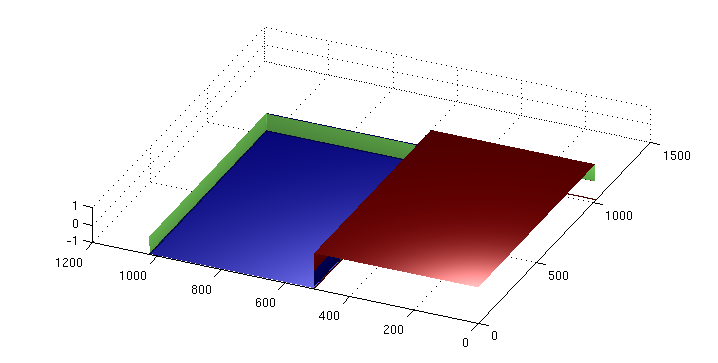
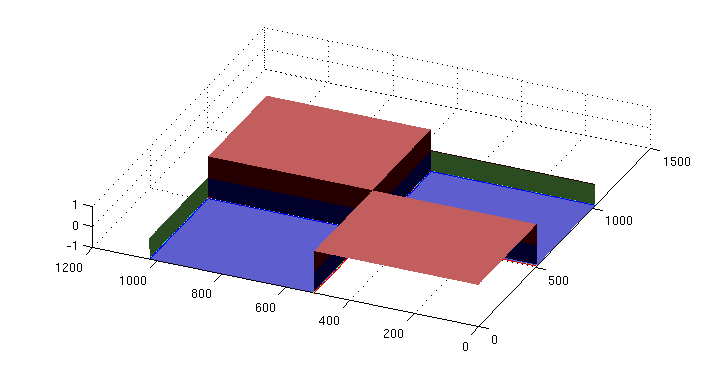
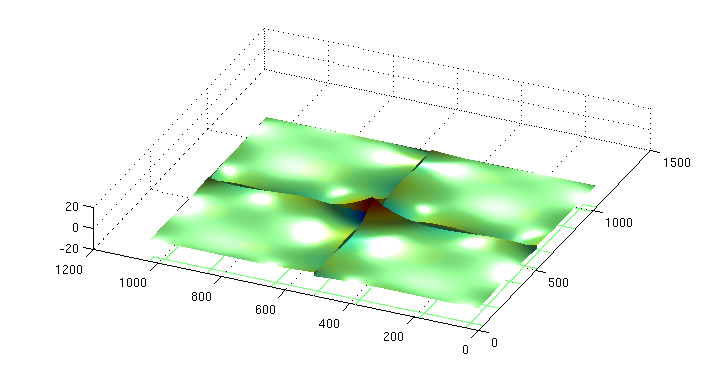
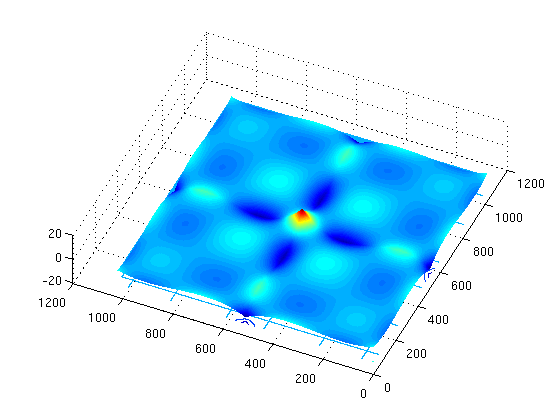
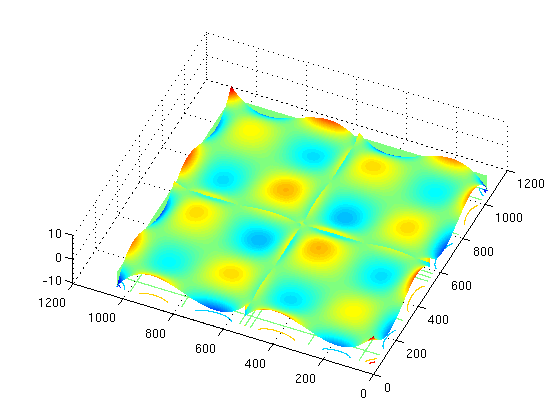
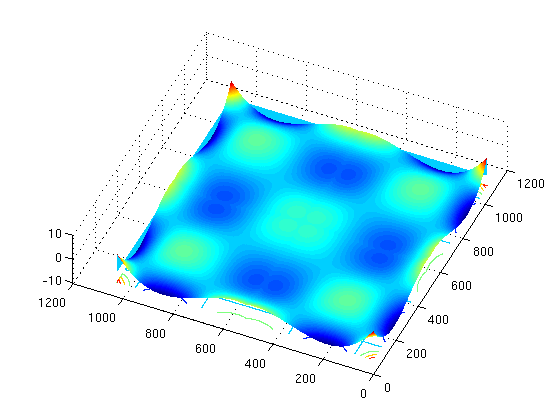
2D Wavelet examples
 haar0x2Dwavelet(:,2) * haar0x2Dgenerator(:,2)' |
 haar0x2Dwavelet(:,2) * haar0x2Dwavelet(:,2)' |
 awavelet0x2D3(:,2) * awavelet0x2D3(:,2)' |
 awavelet0x2D2(:,2) * awavelet0x2D2(:,2)' |
 awavelet0x2D1(:,2) * awavelet0x2D1(:,2)' |
 awavelet0x2D0(:,2) * awavelet0x2D0(:,2)' |
surfc(param[caption], 'EdgeColor', 'none','FaceColor','texturemap')
Solving equations
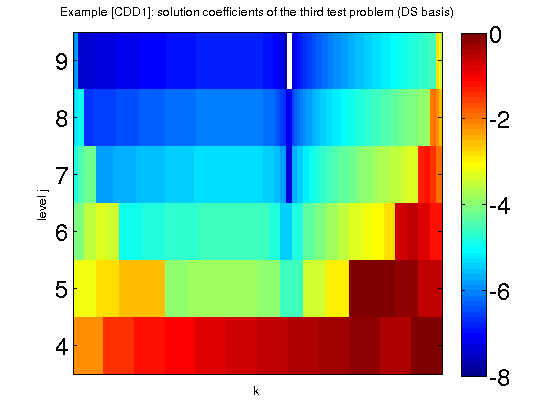
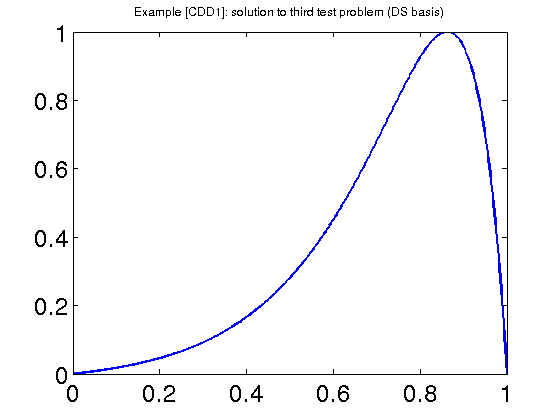
An adaptive algorithm to solve a differential equation
Example of an adaptive algorithm to solve the Poisson equation.
Miscellaneous
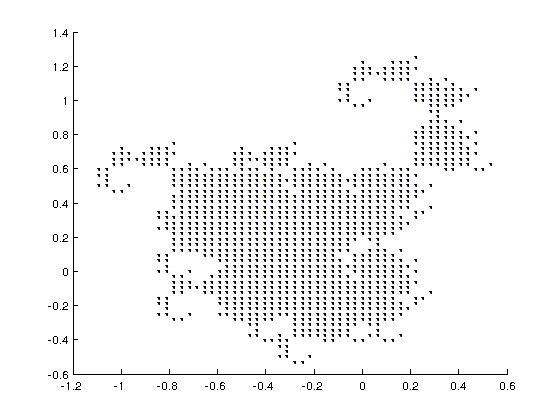
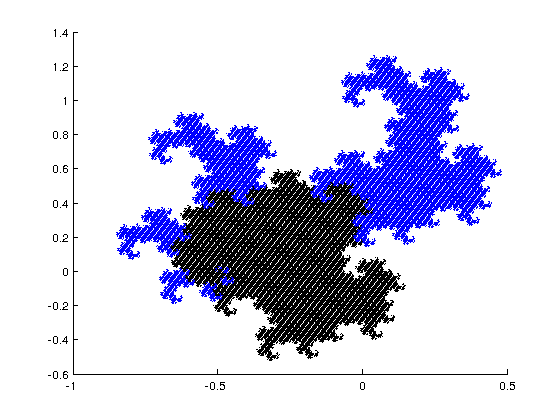
Tiling-Plotter
Self-affine tilings with several tiles (so called "multi-tilings") are useful for wavelet theory due to their connection to multiwavelet bases of L2.
Multi-Tiling-Plotter ZxZ-Tilings Download