 |
 |
 |
 |
Götz Pfander
Professor, Jacobs University
100211
Analysis I, Fall 2010
Overview:
Analysis I/II is
one of the fundamental courses in the mathematical education (together with
Linear Algebra I/II). Its goal is to develop calculus in a rigorous manner
and in sufficient generality to prepare the student for advanced work in
mathematics
Downloadable Course Material:
Announcements:
,
Happy Winter Break, see you next semester.
Instructor:
Götz Pfander,
Research I, Room 112,
Tel. 3211,
Office Hour: Wednesday, 2:15 pm – 3:00 pm (or by appointment).
e-mail: g.pfander@jacobs-university.de.
Teaching Assistant:
Alexandru Sava,
Research I, Room 127,
Office Hour: Appointments via email
e-mail: a.sava@jacobs-university.de.
Lectures:
Tuedsays, 8:15 am, East 4, and Thursdays 11:15 am, East 4
Tutorials:
Mondays, 9:00 pm, QSA in C3
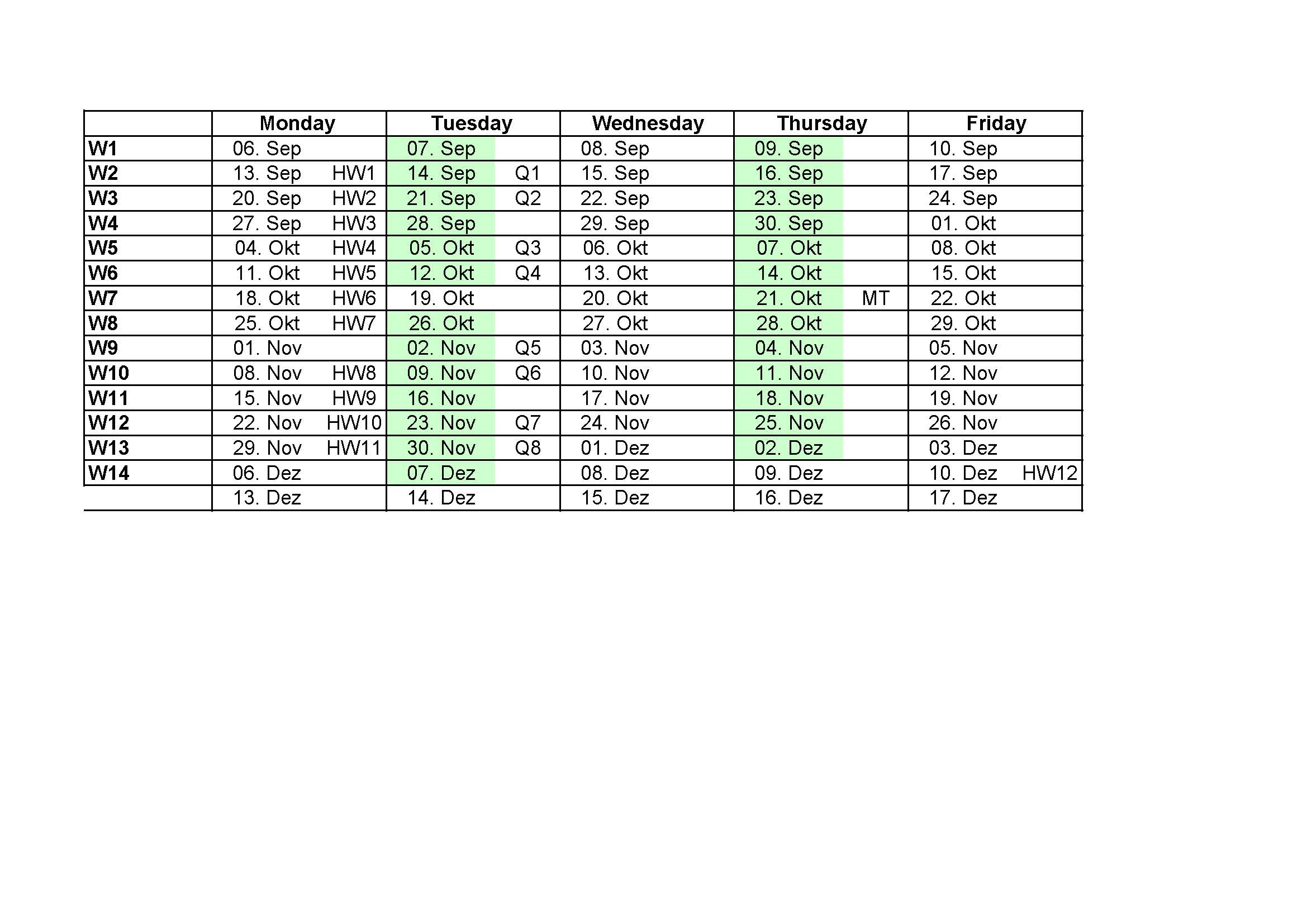
Course Schedule:
Textbooks:
W. Rudin, Principles of Mathematical Analysis, McGraw Hill Text
(The classic textbook, fairly expensive, int. edition ca. 60€)
M. Rosenlicht, Introduction to Analysis, Dover Publications
(Excellent cheap alternative to Rudin, ca 15€)
C. C. Pugh, Real Mathematical Analysis, Springer
(Excellent modern book, my favorite, ca 50€)
www:
http://www.math.jacobs-university.de/pfander/teaching/analysis1_2010.php
Grading:
Your grade is determined by how many points you obtain out of 1000
possible points according to the table on the right. Points can be collected
via Homework (300 pts), Quizzes (180 pts), Midterm Exam (220 pts) and Final
(300 pts). (You can also find a
fill in yourself table here).
Point range
|
Grade
|
||
|
950 |
- |
1000 |
1.00 |
|
905 |
- |
949 |
1.33 |
|
860 |
- |
904 |
1.67 |
|
815 |
- |
859 |
2.00 |
|
770 |
- |
814 |
2.33 |
|
725 |
- |
769 |
2.67 |
|
680 |
- |
724 |
3.00 |
|
635 |
- |
679 |
3.33 |
|
590 |
- |
634 |
3.67 |
|
545 |
- |
589 |
4.00 |
|
500 |
- |
544 |
4.33 |
|
455 |
- |
499 |
4.67 |
|
0 |
- |
454 |
5.00 |
Homework:
Twelve problem sets will be passed out during the semester (see schedule).
Each homework is worth 30 points; your two worst homework scores are dropped.
The homework is due during the Monday tutorials. Deliver it to the Analysis
I mailbox in the lobby of Research 1. Every day you hand in your homework
late
will result in a deduction of 5 points from your final score.
We encourage you to discuss homework problems with fellow students. However, the homework you hand in may not be copied and must reflect your own understanding of the material.
Quizzes:
Eight quizzes will be given in class (see schedule), each carrying
30 points. The best six quizzes will count towards your quiz score (out
of 200).
Quizzes will be approximately 10 minute closed book examinations,
Makeup quizzes are only given if you missed more than three quizzes (excused).
Exams:
The midterm exam is worth 200 points. It will be administered in
class on Monday, October 22nd. The final exam, worth 300 points, will
be scheduled by teh registrar to be held within finals week.
The material used as well as the rules for the exam will be announced one
week prior to the exam.
Prerequisites:
We shall only assume the most basic notions of set theory,
two-valued logic (true or false), proof by induction, epsilon-delta definition
of continuity of real valued functions on the real line, and the arithmetic
of integers and rational numbers. A certain level of mathematical maturity
(achievable through courses such as Foundations of Mathematics) is assumed.
Syllabus:
A sound understanding of the topological and algebraic structure
of the real number system is of fundamental importance to most mathematical
fields! To convey this and some of it’s consequences is the principle
goal of Analysis I / II.
In order to discuss topics such as convergence, continuity, integration and differentiation, a solid understanding of the real number system is needed first. Hence, Analysis I includes an extensive discussion of real numbers, which will then be followed by the introduction of complex numbers.
The concept of distance between two real or complex numbers will lead to the definition of converging sequences and series, and of continuous functions on the real line. These ideas generalize to abstract metric spaces, i.e., sets on which we can assign a distance between any two of its points. Many results in calculus such as the intermediate and maximal value theorem can be generalized to the general (and abstract) metric space setup. Introducing general concepts such as compactness and connectedness have the additional advantage of leading to a better understanding of calculus itself.
The last segment of Analysis I will deal with derivatives of functions on the real line: a function is differentiable if it can locally be approximated well by linear functions. To obtain better approximations one can replace linear functions with higher order polynomials. This will lead to the concept of Taylor polynomials and series.
This course will be roughly divided into the following sections:
I. Relations and functions
II. Real and complex numbers
III. Convergent sequences and series
IV. Metric spaces and continuous functions
V. Differentiation